数模转化器(ADC)供给了许多体系中模仿信号到数字信号的重要转化。它们完结一个模仿输入信号到二元有限长度输出指令的振幅量化,规模一般在6到18b之间,是一个固有的非线性进程。该非线性特性表现为ADC二元输出中的宽带噪声,称作量化噪声,它约束了一个ADC的动态规模。本文描绘了两种时下最盛行的方法来改善实践ADC运用中的量化噪声功能:过采样和高频颤动。
为了解量化噪声缩减法,首要让我们回忆一下,一个抱负的N位ADC的信号与量化噪声比为(单位dB)
SNRQ=6.02N+4.77+20log10(LF)dB,
其间:LF=ADC的输入模仿电压级的加载因子丈量(SNRQ由参考资料1供给)。参数LF界说为模仿输入电压的均方根(RMS)除以ADC的峰值输入电压。当ADC的输入电压为一个能够掩盖转化器满量程电压的正弦曲线,LF=0.707。假定那样的话,SNRQ等式中的终究一项变为?3dB,而且ADC的最大输出信号与噪声比为:
SNRQ-max=6.02N+4.77?3=6.02N+1.77dB。
在技能文献中十分遍及的SNRQ-max公式说明晰为什么工程师要对ADC的SNR运用一个经验值6dB/b。
作为一个运用问题,SNRQ-max公式是不切实践的达观。首要,SNR公式描绘了一个在实践国际中不存在的抱负ADC。第二,在实践运用中,ADC的输入很少会掩盖悉数值。实践国际的模仿信号一般实践上是脉冲信号,而促进ADC的输入变为饱满引发了可大大减小ADC输出SNR的信号切开。可是,本文将假定一个运用大部分输入模仿电压规模的高品质ADC而非研讨最坏情况下的场景。
假定ADC的SNR为6dB/b,下一步是考虑作为或许改善SNRQ的过采样法。减小ADC量化噪声的过采样进程简略直观。模仿信号在fs采样率被数字化,该采样率高于满意Nyquist规范(两倍输入模仿信号带宽)所需的最小采样率,然后被低经过滤。
过采样根据如下假定:一个ADC的总量化噪声功率(方差)为转化器最小有用位(LSB)电压的平方除以12:
总量化噪声功率=σ2=(LSB value)/12
过采样相同假定量化噪声值是实在随机的;这意味着在频率规模内,量化噪声有一个滑润的频谱。(假如ADC是由一个掩盖转化器模仿输入电压规模重要部分的模仿信号驱动且周期性不显着,该假定有用)。
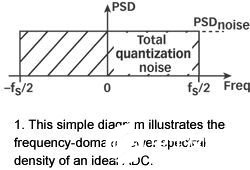
图1显现了量化噪声的另一方面,功率频谱密度(PSD)。这是在每Hz噪声功率下丈量的量化噪声的频率规模特征。运用PSD,量化噪声能够被表明为每单位带宽的功率巨细。随机噪声假定得到的总量化噪声(根据转化器LSB电压的固定值)被均匀散布在频率规模内,从?fs/2到+fs/2,如图1所示。该量化噪声PSD的振幅为总量化噪声功率除以总带宽fs,其间振幅呈现在总带宽上:
PSDnoise=[(LSB value)2/12](1/fs)=(LSB value)2/12fs 单位为W/Hz。
下一个问题是:“怎样才能减小PSDnoise等级?”运用一个具有附加位分化的ADC,能够减小分子中的LSB值,这个ADC将减小LSD值相同也减小PSDnoise。不过这是一个贵重的解决方法。更好的方法是用更高采样率来增大分母。
选用更高采样率的成果在图2(a)顶用初级离散信号表明。经过将ADC的fs,old 采样率添加到某一更高值fs,new (过采样),总噪声功率(一个不变值)被散布在一个广泛的频率规模内[图2(b)]。由于一个转化器的总量化噪声功率仅依赖于位数而不是采样率,图2(a)和2(b)中昏暗曲线下的面积持平。将一个低经过率器放在转化器的输出来减小量化噪声等级对信号的危害。
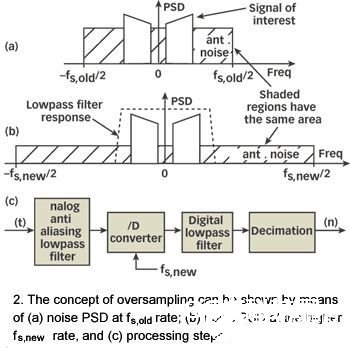
经过过采样得到改善的信号与量化噪声比为,以dB为单位:
SNRQ-gain =10log10(fs,new /fs,old )。
SNRQ-gain 表达式的出处在参考资料1中供给。作为一个SNR的函数,N位ADC的位数大约是SNR/6,因此总有用位数为10log(M)/6+N,其间M=fs,new /fs old ,。这意味着假如采样率M为2,则ADC的有用位数是Nos=0.5+N。运用因数为2的过采样,可取得在有用SNR中的一半位。取得一个特别的K额定有用位数所需的过采样率M由式子M=4K得出,因此有用位数为Nos=K+N。
举例说明,假如fs,old =100kHz,且fs,new=400kHz,SNRQ-gain =10log10(4)=6.02dB。这样,因数为4的过采样(和过滤)将量化噪声减小到1b。然后,有或许由一个N位ADC得到N+1位的功能,由于信号振幅分化是以更高采样速度为价值得到的。经过数字过滤后,输出信号能够被减小到初级fs,old 而不会有损改善了的SNR。
当然,为了能从过采样计划中获益,用于低通滤波器系数和寄存器的位数必需超越ADC的初始位数。经过运用依赖于用x(t)表明的搅扰模仿噪声的数字低经过率器,就有或许选用图2(c)中与低采样率下所需的模仿过滤器相对的低功能(更简略)模仿抗混迭滤波器。
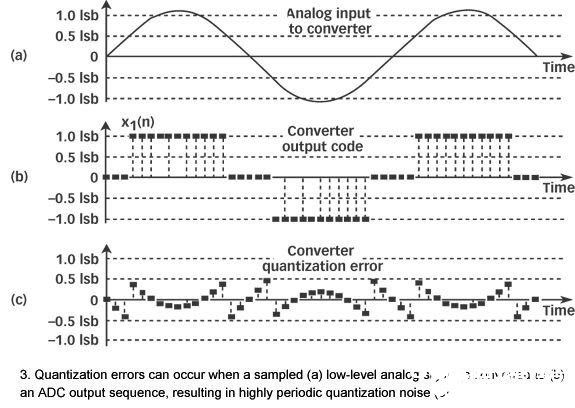
第二个用来最小化ADC量化噪声影响的技能是高频颤动,它在进行模仿数字转化前将噪声参加模仿信号。一个比如是,图3(a)中显现的数字化初级模仿正弦信号。该信号的峰值电压刚刚超越了单个ADC的LSB电压级,引起转化器输出x1 (n)个样本。由于高峰值正弦电压级,x1(n)输出序列被省掉,而且在其频谱规模内发生谱谐波,该谐波与图3(c)中的量化噪声周期相同很显着。
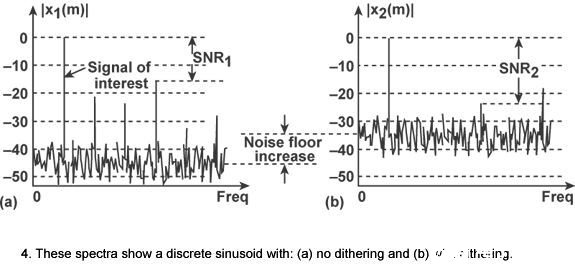
图4(a)显现x1(n)的频谱,以dB为单位,在那里乱真量化噪声谐波十分显着。均匀多频谱不或许将某些频谱重视的部分提升到那些乱真谐波级之上,注意到这点很有所值。由于量化噪声与输入正弦波严密相关,量化噪声的时刻周期与输入正弦波相同,频谱均匀相同也会进步噪声谐波级。但是高频颤动将供给协助。
高频颤动的成果为一个跳过附加转化器LSB边界且发生更随机量化噪声的噪声模仿信号,以及下降不期望呈现的频谱谐波级[图4(b)]。颤动进步了均匀频谱噪声基数但却使SNR2添加。颤动迫使量化噪声损失其与初始输入信号的一致性,假如想要的话,该一致性将会从均匀化中获益。
当数字化低振幅模仿信号,长周期模仿信号(比如在采样时刻距离中有偶数周期的正弦波),和改变缓慢的(低频或DC)模仿信号时,高频颤动十分有用。图5(a)显现了高频颤动的规范履行。由噪声二极管或噪声发生器集成电路供给,用于该进程的很多随机宽带模仿噪声具有一个峰到峰值为1/3-to-1LSB电压级。
Wannamaker现已表明运用TPDF的颤动处理睬导致具有不变零均值和独立于输入信号特征的不变(非零)功率的量化噪声。这些都是量化噪声十分等待的特性;前者确保数字转化器的输出均匀起来等于输入;后者确保将不会呈现“噪声调制”。噪声调制在量化噪声的功率依赖于信号或许被信号调制时呈现。这对音频信号来说具有理性含义,而且一般是不需要的。
对苛求的高功能音频运用来说,工程师现已发现该类型的颤动是抱负的。它能够经过从两个别离的,独立的,均匀散布的(也称作矩形PDF)噪声发生器添加颤动噪声发生。两个独立噪声源之和的PDF是它们各自PDF的卷积。由于两个矩形函数的卷积是三角形的,这个双噪声源颤动计划发生所需的TPDF。抱负的TPDF颤动噪声具有刚好两个LSB电压级的峰对峰级。
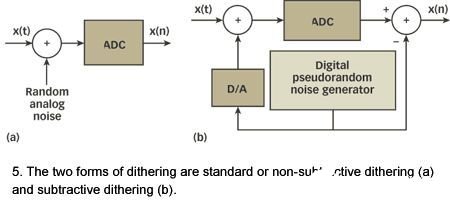
在重视信号占有了全频带0到fs/2中某些已清晰界说部分的情况下,发射具有等同于4到6LSB电压级的峰对峰值,和具有信号带外部频谱能量的频谱状颤动噪声将是有利的。Wannamaker给出了“过滤颤动”特征的充沛(非必要)条件,这将确保作为成果的量化噪声功率独立于信号,而且显现外加一个常量(以频率为单位)噪声功率后,终究的颤动噪声频谱将在形状上类似于量化噪声频谱。来自正弦波信号的量化噪声将发生额定的乱真谐音!然后,该窄带颤动噪声能够由后继的信号过滤消除。
本文中评论的高频颤动类型被人们认为是“非负颤动”(NSD)。图5(b)说明晰被称为“负颤动”(SD)的另一种运用颤动方法。一个SD体系具有一切颤动的长处(随机化了量化噪声),却没有它的任何缺陷(未添加全体噪声功率)。Wannamaker说明晰有恰当特性的负颤动将怎么得到频谱空白和均匀散布的总量化噪声。
责任编辑:gt