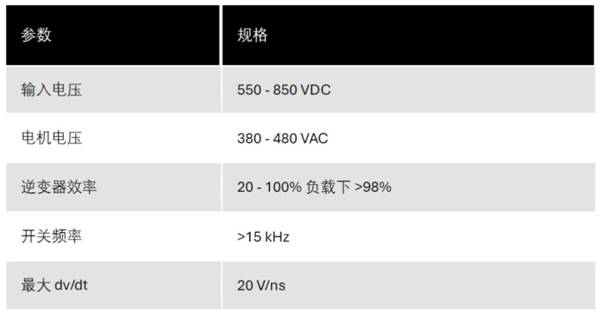
沟通阻抗法是指操控经过电化学体系的电流(或体系的电势)在小幅度的条件下随时刻按正弦规则改动,一起丈量相应的体系电势(或电流)随时刻的改动,或许直接丈量体系的沟通阻抗(或导纳),从而剖析电化学体系的反响机理、核算体系的相关参数。
沟通阻抗法包括两类技能,电化学阻抗谱和沟通伏安法。电化学阻抗谱技能是在某一直流极化条件下,特别是在平衡电势条件下,研讨电化学体系的沟通阻抗随频率的改动联系;而沟通伏安法则是在某一选定的频率下,研讨沟通电流的振幅和相位随直流极化电势的改动联系。这两类办法的共同点在于都应用了小幅度的正弦沟通鼓励信号,依据电化学体系的沟通阻抗概念进行研讨。
沟通阻抗法基本原理
一个不知道内部结构的物理体系就像一个黑箱。这个黑箱中心存放着什么东西以及这些东西是怎么摆放的都是看不见的。这便是说,这个黑箱的内部结构是不知道的。可是,作为物理体系的这个黑箱有一个输入端及一个输出端。当咱们从黑箱的输入端给它一个扰动信号,那么咱们就能从黑箱的输出端得到一个信号输出。假如这个黑箱的内部结构是线性的安稳结构,输出的信号便是扰动信号的线性函数,所以这个输出的信号就被称为黑箱对扰动信号的线性呼应或简称呼应。对黑箱的扰动及黑箱的呼应都是可丈量的。因而,人们能够在不知道黑箱内部结构的状况下,经过扰动与呼应之间的联系来研讨黑箱的一些性质。
在科学研讨中,人们用来描绘对物理体系的扰动与物理体系的呼应之间的联系的函数,被称为传输函数。一个体系的传输函数,由体系的内部结构所决议,且反映了这个体系的一些性质。假如体系的内部结构安稳,体系的输出信号与输入它的扰动信号之间具有因果联系,并且两者间是线性联系,那么经过丈量就比较简单研讨这个传输函数。能够用式 R=H(s)P 一般地表明对一个物理体系的扰动与物理体系对扰动的呼应之间的联系。式中,R和P分别为呼应函数与扰动函数的拉普拉斯(Laplace)改换;H(S)是传输函数,它是拉普拉斯频率S的函数。应该阐明,这儿所指的扰动能够是任何品种的扰动,它能够是电信号、光信号或其他信号;扰动的办法也能够是多种多样的,能够是单个的或周期的脉冲、方波阶跃、方波沟通、三角波沟通或正弦波沟通等。
电化学阻抗谱理论便是经过对电池体系施加小幅电位扰动,经过输入的电位函数和测得的输出电流函数求得体系的传递函数。假如扰动是正弦波,那么此刻传输函数称为频率呼应函数或简称为频响函数。现考虑正弦波的扰动与呼应都是电信号的状况。关于一个安稳的线性体系M,加以一个角频率ω的正弦波电信号(电压或电流),X为鼓励信号输入该体系,则相应地从该体系输出一个角频率也是ω的正弦波呼应电信号(电流或电压)Y。Y与X之间的联系能够用式 Y=G(ω)X 来表明。式中的G为频响函数,它反映体系M的频响特性,由M的内部结构所决议。因而能够从G随X与Y的频率f或角频率ω改动状况来取得线性体系内部结构的有用信息。假如扰动信号X为正弦波电流信号,而Y为正弦波电压信号,则称G为体系M的阻抗。
实际上,体系需求满意三个基本条件的状况下,才干确保对体系的扰动及体系的呼应都是角频率为钠正弦波信号。
(1)因果性
体系输出的信号仅仅关于所给的扰动信号的呼应。这个条件要求在丈量对体系施加扰动信号的呼应信号时,有必要扫除任何其他噪声信号的搅扰,确保对体系的扰动与体系对扰动的呼应之间的联系是仅有的因果联系。很明显,假如体系还受其他噪声信号的搅扰,则会打乱体系的呼应,就不能确保体系会输出一个与扰动信号具有相同角频率的正弦波呼应信号。
(2)线性
线性体系输出的呼应信号与输入体系的扰动信号之间应存在线性函数联系。正是因为这个条件,在扰动信号与呼应信号之间具有因果联系的状况下,两者是具有同一角频率确正弦波信号。假如在扰动信号与呼应信号之间尽管满意因果性条件但不满意线性条件,呼应信号中就不只具有频率为ω的正弦波沟通信号,还包括其谐波。应该注意到电极进程的电流密度与电位之间不是线性联系。只要在电位信号的正弦波的幅值很小的条件下两者近似地为线性。故为满意线性条件,电化学阻抗谱丈量时电位的正弦波信号的幅值一般不超越5mV。
(3)安稳性
安稳性条件要求对体系的扰动不会引起体系内部结构产生改动,因而当关于体系的扰动中止后,体系能够康复到它原先的状况。一个不能满意安稳性条件的体系,亦受鼓励信号的扰动后会改动体系的内部结构,因而体系的传输特征并不是反映体系固有的结构的特征,并且中止丈量后也不再能回到它本来的状况。在这种状况下,就不能再由传输函数来描绘体系的呼应特性。

关于动力电池沟通阻抗法的基本原理剖析
沟通阻抗办法被广泛应用于电极进程动力学的研讨,特别适合于剖析杂乱电极进程。它能够协助咱们了解界面的物理性质及所产生的电化学反响的状况(如电极反响的办法,分散系数,沟通电流密度的巨细等)。
沟通阻抗办法是施加一个小振幅的正弦沟通信号,使电极电位在平衡电极电位邻近微扰,在到达安稳状况后,丈量其呼应电流(或电压)信号的振幅和相,顺次核算出电极的复阻抗。然后依据想象的等效电路,经过阻抗谱的剖析和参数拟合,求出电极反响的动力学参数。因为这种办法运用的电信号振幅很小,又是在平衡电极电位邻近,因而电流与电位之间的联系往往能够线性化,这给动力学参数的丈量和剖析带来很大便利。
二次锂离子电池的充放电进程中,锂离子在正极资料上的嵌入反响是:锂离子从液态电解质内部搬迁到电解液与固体电极的交界面;锂离子在电极/电解液界面处吸附构成外表层;吸附态的锂离子进入正极资料;锂离子由固体电极外表向内部分散。脱出反响为上述进程的逆进程。以上几个进程分别在不同程度上影响电极体系的动力学功能,在电解液相同的状况下,电极进程的动力学参数取决于电极资料及其界面性质。
假如电极反响只受界面电荷搬迁和物质分散所分配,则其典型的复数阻抗图如图9-21所示。图中的RE为溶液电阻,Rct为界面反响电阻,Zw表明锂离子在界面邻近分散的Warburg阻抗,因为锂离子在电解质中的分散速率远大于在固相活性物质中的分散速率,因而能够为Zw描绘的是锂离子在固相活性物质中的分散进程。所以经过沟通阻抗法能够核算锂离子在固相资猜中的分散系数。