用的是线性时不变的电容。慨叹,岁月不饶人,什么电容电感、微分方程早舍吾回忆而去。
1 电容充电进程
当电容器接通电源今后,在电场力的效果下,与电源正极相接电容器极板的自由电子将经过电源移到与电源负极相接的极板下,正极因为失掉负电荷而带正电,负极因为取得负电荷而带负电,正、负极板所带电荷巨细持平,符号相反。电荷定向移动构成电流,因为同性电荷的排挤效果,所以开端电流最大,今后逐步减小,在电荷移动进程中,电容器极板贮存的电荷不断添加,电容器两极板间电压 Uc等于电源电压 U时电荷中止移动,电流为0。
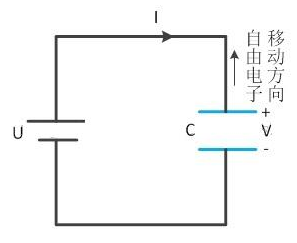
Figure1. 电容充电进程–自由电子流过电源的移动
如Figure 1所示,当给U一个电压值的一会儿,电路必需要满意基尔霍夫电压规律,因此电容两头电压产生逼迫跳变,其值变为U。所以,Figure 1的电路充电时刻极短,简直为0。
2 RC电路作为芯片复位电路
(1) RC电路充电
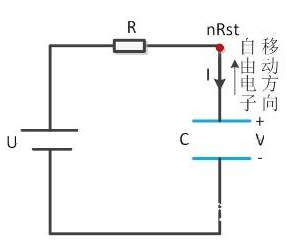
Figure2. RC电路电容充电进程
[1] U = 0时,电路无通路。nRst点与任何一点都不存在电位差。
[2] 在给U一个电压的瞬间,电容正极板上有电子经过点电源抵达负极板然后构成回路,此刻电源电压U的值将分配在电阻R和电容C之上。nRst点的电压与电容正极板的电压值持平。
[3] 跟着自由电子的移动,电容充电结束,不再有电流即电路中又无通路。此刻V = U,电阻相当于导线。nRst点与电容负极的电位差为U。
RC电路电容的充电进程也很短,但比纯C电路的进程要长。这个时刻可以经过基尔霍夫规律算出来:
R * I(t) + V(T) = U
I(t) = C * dV(t) / dt
得
R * C dV(t) / dt + V(T) = U (1)
这是一个一阶线性非齐次(U !=0)微分方程。
首要,先评论(1)中对应的齐次方程
R * C dV(t) / dt + V(T) = 0
别离变量得
dV(t) / V(t) = – dt / RC
对两头积分得
lnV(t) = (- 1 / RC) Sdt + lnc
得
V(t) = e-(t/RC) + lnc
= A * e-(t/RC)
对方程两头进行微分,得:
dV(t) / dt = -(A/RC) * e-(t/RC)
然后将上式带入(1)中得
V(t) = U + A * e-(t/RC)
连抄再讨教,总算将这个方程解出来了。当V(t) = U时,表明电容充电进程结束。这个时刻跟R * C值有关。
(2) RC电路用作芯片复位电路
经过复位引脚对芯片(如STM32103)进行复位要满意两点[详细要求以芯片的手册为准]:
复位引脚为低电平(电压小于3.3V)
坚持满足长的时刻(详细时刻可检查其手册)
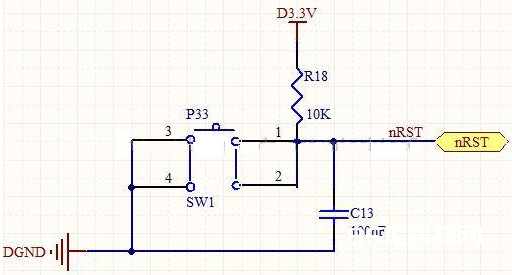
Figure3. RC电路用于复位电路图
[1]当3.3v电源加到图示方位时,RC电路导通,nRST与地的电位差为电容与地的电位差。nRST与地的电位差只需电容充电结束后才会到达3.3V,所以在电容的充电进程中,给芯片引脚的信号都是低电平。依据RC电路充电方程式V(t) = U + A * e-(t/RC),只需合理的挑选好R跟C的值就可以确保充电时刻大于芯片复位所要求的时刻。检查e-(t/RC)的衰减曲线:

Figure4. A * e-(t/RC)衰减进程
虽然A应该是负值,但上图可以表明其衰减进程。可以看到,当t = 4RC时,整个表达式的值就现已很接近于0。所以,只需电路中的4RC乘积大于芯片要求复位时刻即可。考虑在电容充电进程中应尽量将U电压分配到电阻R上,所以应将电阻R的值选得大一些。图示中4RC = 4 * 10000 * 10^-5 s = 0.4s。这个比按键复位还有确保。
[2] 电路上电后即电容充电结束后,若再想对芯片复位则只需按下P33即可,按下P33的进程中nRST接地。人按键的速度大于10ms(按键程序用10m s消颤动),而一般芯片复位要求的时刻都比较小,应该远小于10ms。所以,按键复位可以确保芯片的复位。
这便是常见的使用RC电路作为芯片复位的原理。分为上电复位和按键复位。仍是摆脱不了微分方程的魔掌啊~









