卢嘉轩,李 晋,周 延
(上海大学 机电工程与主动化学院 工程练习国家级教育试验演示中心,上海 200444)
摘要:针对一种物联网医疗箱体系,提出了一套运用机器学习和蚁群算法的药物调度办法。该办法运用阈值区别的办法,对取药记载树立了岭回归、随机森林回归和神经网络的混合模型,以猜测不同医疗箱中各类药物的需求量。之后,依据硬件检测的药物实践数量,核算出各药物的差错值,在将调度问题转化为旅行商问题今后,别离运用根本蚁群算法和最大最小蚁群算法对调度问题进行了求解和比照。试验标明,该办法能较好地猜测药物的需求量,规划出一条合理的药物调度途径,为物联网医疗箱体系的药物调度供给了一种数据驱动的处理计划。
关键词:蚁群算法;机器学习;物联网医疗箱;调度;旅行商问题
0 导言
跟着智能医疗概念的鼓起,主动售药机和自助医疗箱在英美等国得到了广泛推行,在我国也逐步遍及。可是,传统主动售药机在日常运营中需求进行人为的药物检查和补给,在药物的调度上也没有一套较为适宜的计划。除此之外,因为地舆约束和宣扬力度欠佳,售药机常常无人问津,运用率较低。为此,一种依据物联网的学校医疗箱体系应运而生,该体系由若干放置在学校不同方位的联网的医疗箱所组成,可以在短时刻内为师生突发的伤口供给及时有用的救治药物及必要的救援用具。该药物箱体系已在某高校进行了试运营,用户可以经过微信小程序的终端检查邻近的药物箱方位和药物余量,一切取药记载也将上传至服务器,保存在数据库中。
本文依据该新式物联网医疗箱体系,提出了一种依据前史取药记载和药物余量进行调度的通用办法。该办法分为药物需求量猜测和药物调度途径规划两大进程。在需求量猜测的试验中,针对前史取药记载,树立了岭回归、随机森林回归和神经网络的混合模型,以猜测各医疗箱中药物的需求量。在调度途径规划的试验中,将猜测的药物需求量与实践数量进行比较,将差错量界说为药物实践数量与猜测需求量之差。该办法将药物的调度问题转化为多个供货商和多个需求者之间的特别旅行商问题(Traveling Salesman Problem,TSP),并别离运用根本蚁群算法(Ant System,AS) [2] 和最大-最小蚁群算法(Max-Min Ant System,MMAS) [2-5] 进行了求解和比照。该办法能为新式物联网医疗箱体系的药物分配与调度供给处理计划,有用下降日常运营本钱。
1 需求量猜测
因为物联网医疗箱具有药物检测、数据上传的特色,因而一切的取药记载和药物余量都会保存在云服务器中,这也为模型的树立供给了必要的数据支撑。关于某类存放于医疗箱中的药品,影响其需求量的要素可以大致归纳为3类:所在时刻,医疗箱地舆方位和药物本身特性。针对医疗箱体系而言,取药记载间接地反映了特定时刻、特定地舆方位上各类药品的需求量。为此,可以经过前史取药记载的数据,树立上述3类要素到药品需求量的映射联系。
详细地,所在时刻包含前史取药日期以及对应的月份和星期;地舆方位包含医疗箱所在的经纬度数值和地舆画像,如地图爱好点(Point of Interest,POI)密度、是否坐落宿舍、食堂、运动场、体育馆、试验室等特别场所等;药物本身特性,包含药物所属的类别以及由职业认可的药物评定数据库供给的药物评分等。在获取并整合上述数据今后,即可以运用机器学习算法构建药品需求量与各要素之间的模型,即经过输入上述特征来猜测特定日期、特定地舆方位下某药品的日需求量或多日需求量。本文运用的模型包含岭回归、随机森林回归和神经网络。
岭回归(Ridge Regression) [9] 是线性回归问题中一种改善的最小二乘估量法,即在最小二乘估量法的丢失函数中加上L2正则项,经过抛弃最小二乘法的无偏性为价值以取得更适宜的回归系数,防止过拟合。岭回归因为可供练习的参数较少,在数据量不太大、线性可分性强的问题上体现较优。
随机森林回归(Random Forest Regression) [9-11]是一种针对分类与回归树(CART,Classification AndRegression Tree)进行集成的办法,经过取每棵CART回归树叶子结点的均值来得到猜测值。比较于运用最小化基尼系数来挑选特征的CART树,随机森林往往具有更强的泛化才能,在处理回归问题上也具有较好的通用性。
神经网络(Neural Networks,NNs) [9,10,12] 也称人工神经网络,是一种仿照大脑神经突触联接的结构进行信息处理的数学模型。该网络运用很多根本神经元进行核算,并能经过反应机制来优化网络参数,具有学习的才能。深度神经网络在具有大规划练习数据的使命上体现杰出,但因为可供练习的参数数量巨大,在数据量过小的使命中或许逊于一般的机器学习算法。
因为不同医疗箱中的药品讨取量和需求量或许不在同一个量级上,运用单一模型进行猜测并不适宜。为此,本文选用阈值区别的办法,针对数据量小于某个阈值的药品,选用简略的岭回归模型进行猜测;而针对数据量大于该阈值的药品,选用较为杂乱的随机森林回归和神经网络一起进行猜测,并把这两个模型输出的均值作为终究的猜测值。试验标明,这种办法能取得比单一模型更高的准确率。
2 调度途径规划
2.1 问题描绘与建模
物联网医疗箱的药品调度是医疗箱体系日常运营中的关键问题,首要包含数量和途径两大难题,即需求向各医疗箱投进多少药品以及怎么规划投进和调度的途径。在传统的主动售药机形式中,运营方需求事前预估各售药机的药品需求规划,并人为地对药品的余量进行检查和弥补,是一种依据经历的办法。而在数据驱动的物联网医疗箱体系之下,因为一切的药品需求量可以由已练习的网络核算得出,因而可以将猜测值与硬件检测的实践药品数量进行比对,确认各类药物的供需联系。
为此,本文假定医疗箱中的药品数量需求满意该药品N日内的需求,并界说医疗箱k中药品的差错量β k,i 为当时该药品的实践数量与该药品N日需求总量之差,即

其间,r k,i 为医疗箱k中当时药品i的实践数量,可以由硬件检测并上传数据库获取得到;p k,i 为猜测的医疗箱k中药品i的日均匀需求量。若β k,i 大于0,标明该医疗箱中的这类药品处于供大于求的状况,可以调出;若β k,i 小于0,则标明该药品处于紧缺状况,希望调入。由此,医疗箱体系的药物调度问题即可转化为一个特别的旅行商问题(TSP),即派一辆小车从特定站点动身,拜访各医疗箱和药房、医院、库房等药物供给站点,寻觅出总旅程最短的Hamilton圈,并在这个进程中完结药物的调度。
设G=(C,L)是一个有向图,其间 C ={ c 1 , c 2 ,⋯,c m }为m个医疗箱或供给站点的调集,L={l ij |c i ,c j ∈C为调集C中元素两两连线构成的边集, d i,j ( i,j =1,2,…, m )为医疗箱 i 和j 之间 l ij 的行车间隔,可以经过调用地图软件API接口获取其数值。在传统的TSP问题中,一切的站点是没有区别性的,即可以恣意挑选站点作为途径的连续。而在本问题中,因为需求进行药物的调度,因而关于候选站点k的挑选有如下的约束条件:
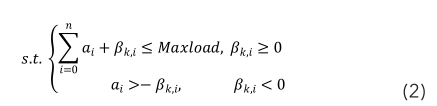
其间,a i 为当时卡车上已有药物i的数量,β k,i 为医疗箱k中药品i的差错量,Maxload为卡车的负载量上限。当结点k的差错量大于等于0,即该药品供大于求时,需求将其移上卡车,要求移上卡车后药品总数量不超越卡车的最大负载量;当结点k的差错量小于0,即该药品求过于供时,要求卡车上有足够多的该类药物以补给医疗箱。
假如一个医疗箱中一切药品都满意上述约束条件,且该站点还未拜访,则称该站点为该时刻的有用候选站点。
调度途径查找的方针便是不断挑选有用候选站点,直到一切站点都已被拜访。
2.2 根本蚁群算法
蚁群算法(Ant System,AS)是一种模仿进化的算法,由意大利学者多里科(Marco Dorigo)于1991年提出,经过模仿蚂蚁在寻食进程中开释信息素优化途径的行为,构建了一套人工的蚂蚁体系。蚁群算法在求解TSP问题中得到了广泛使用,也因而作为本文医疗箱药物调度问题的根本求解算法。
在算法的开端,将q只蚂蚁随机地置于m个医疗箱站点上。关于每只蚂蚁,都具有一张归于自己的忌讳表tabu k ,用来表明蚂蚁k现已拜访过的医疗箱站点。在本问题中,因为候选站点的约束条件约束,因而需求额定设置一张无效候选站点表invalid k 作为不满意公式(2)的候选站点的调集。
在t时刻,在医疗箱 i 处的蚂蚁 k 需求依据该时刻的有用候选站点集J k (i),依据某一概率函数挑选下一个站点j。其间,有用候选站点集J k (i)为去除了忌讳表中元素和无效候选站点表invalid k 中一切元素的站点调集,即
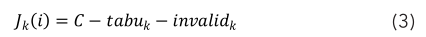
蚂蚁从站点搬运到站点的搬运概率界说为:
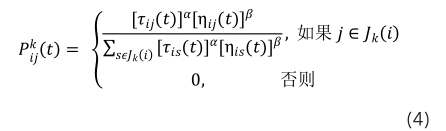
不然其间, α 为信息启示式因子,表明轨道的相对重要性;β 为希望启示式因子,表明能见度的相对重要性; η ij (t)是启示函数,表明蚂蚁 k 从站点 i 搬运到站点 j 的希望程度,这儿取站点 i 和站点 j 实践行车间隔的倒数,即

式中,站点 i 到站点 j 实践行车间隔 d i,j 越小,则 η ij (t) 越大,因而 η ij (t) 可以表明为蚂蚁从站点i搬运到站点j的希望程度。
在算法的开端阶段,一切边上的信息素量是持平的,即 τ ij (0)=C ( C 为常数)。当一切蚂蚁都寻觅到一条Hamilton回路后,各途径的信息素量依据下式来更新:
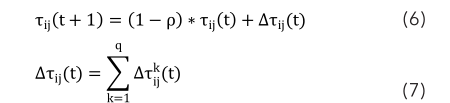
其间, ρ 为信息素的蒸腾系数, Δτ ij (t) 为本次迭代中边 l ij上信息素的增量, Δ 为蚂蚁 k 在本次迭代中留在边l ij 上的信息素。在Ant-Cycle模型中,界说为:

式中, Q 为正常数,表明信息素的强度; L k 为蚂蚁 k 在本次迭代中所经途径的总长度。在每一轮迭代中,一切的蚂蚁都去寻觅一条Hamilton回路,并更新信息素,开端下一轮迭代。当迭代次序到达最大进化次数时,算法完毕,当时的最优Hamilton回路即为算法寻觅到的最优调度途径。
2.3 最大最小蚁群算法
根本蚁群算法供给了一种求解TSP问题的计划,可是其存在收敛速度较慢、易陷于部分最优的缺陷。为此,Stutzle和Hoos提出了最大-最小蚂蚁体系(Max-MinAnt System, MMAS)。相较于根本蚁群算法(AS),最大最小蚁群算法做了如下改善:
1)选用大局信息素更新,即在每一轮迭代完毕后,仅更新本轮或大局最优解途径上的信息素,以加强最优解的影响力,行将式(6)和(7)修改为:
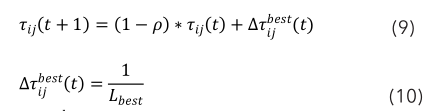
其间,为本次迭代中最优途径或大局最优途径上信息素的增量,其值等于最优途径的总长度 L best 的倒数。
2) 约束每条边上的信息素在固定规模[τ min ,τ max ]内,防止某条途径上的信息素量远大于其他途径,形成算法过早收敛于部分最优解。
3)将初始时刻各条边上的信息素量τ ij (0)设为τ max ,而不再是一恣意的常数 C ,使算法在初始阶段能具有较高的随机性,以进步发现大局最优解的概率。
3 试验与成果剖析
3.1 数据描绘与预处理
本文的试验数据来源于正在上海大学宝山校区试运营的医疗箱体系后台,因为用户需求运用微信小程序进行取药,因而一切的取药记载都会保存在云服务器的MySQL数据库中。取药记载包含取药时刻、医疗箱编号、药物编号、药物称号等字段。本试验运用Python拜访数据库,读取取药记载,并进行了数据的处理和整合,核算出了各医疗箱中各类药物的均匀日讨取量。
针对取药日期,将其转化为项目开端运营到该日期的差错天数,并参加该日期所对应的月份和星期作为模型的输入字段;针对医疗箱方位,调用经纬度转化函数将其编码为可以用单个字段反映地舆坐标的GeoHash格局 [13] ;针对医疗箱所在方位的特别地舆类型,如运动场、游泳馆、试验室、宿舍等,别离进行One-Hot编码将其转化为8个字段;针对药物评分,经过API接口调用了全球药物评定数据库SERMO的相关评分数据。
为了更好地描写医疗箱的地舆画像,本试验调用Google地图接口分类核算了各医疗箱地舆坐标邻近的爱好点(POI)数量,包含餐饮类数量、公司企业类数量、购物商场类数量、交通设施类数量、路途地名类数量等。最终,将一切上述字段和对应的日讨取量进行归一化处理以消除量纲的影响。
3.2 需求量猜测
本文假定前史取药记载中的讨取量间接地反映了特定医疗箱中该药品的需求量,希望可以构建一个由上述特征到药物日均匀需求量的映射联系。因为经预处理后的特征向量维数过高,本文运用主成分剖析(Principalcomponents analysis,PCA)的办法对特征向量进行降维,并以8:2的份额区别练习集和测验集。


本试验中,设定区别阈值为 w ,即练习会集数据条目少于的 w 药品,运用岭回归进行建模,不然别离运用随机森林回归和神经网络进行建模与猜测。其间,岭回归和随机森林由Python的机器学习库Scikit-learn完成,随机森林的子模型数n_estimators设为30;神经网络运用Keras框架下的反向传达算法(BP)进行完成,包含输入层和输出层共6层,每层的神经元个数别离为[31,100,50,30,10,1],激活函数运用ReLU函数,梯度优化运用Adam算法,本文运用均方根差错(RMSE)来衡量模型的猜测精度,即

式中, p gt,i 为实在的药品均匀日需求量, p model,i 为模型猜测出的药品日需求量。本试验依据上述参数设置,调整区别阈值w,针对数据量小于w的药品一致运用岭回归进行建模,针对其他药品别离运用随机森林回归、神经网络、随机森林与神经网络取均值的算法进行了试验,核算出了一切药品的全体均方根差错,如表1所示。
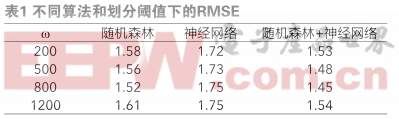
3.3蚁群算法途径调度
在得到各医疗箱中各类药品的日需求量,即可依据硬件检测的实践数量核算出各类药品的差错值。试验中假定 N =7,n =5,即每个药物箱中共有5件药品,要求调度完毕后每件药品可以满意7日的需求量。因为当时物联网医疗箱仅在上海大学宝山校区试点运营,数量不多,因而本文模仿了50个医疗箱和药品供给商的站点,以查验蚁群算法的调度作用。本试验运用Python的图形化GUI库Tkinter别离编写了根本蚁群算法和最大最小蚁群算法,程序界面如图1所示。
图 中 每 个 站 点 上 方 的 五 元 组( β k,1, β k,2 ,β k,3 ,β k,4 ,β k,5 )表明当时医疗箱 k 中5件药品的差错值,其间黑色填充的结点代表卡车的开端结点。以运用根本蚁群算法,设置蚂蚁种群数q=50,卡车最大负载量 Maxload =800,信息启示因子 α =1.0,希望启示因子 β =1.0,信息素强度 Q =100为例,得到的最优调度总间隔为4501,调度途径如图2所示。
为了比较根本蚁群算法(AS)和最大最小蚁群算法(MMAS)在该问题上的作用,本文别离就不同的卡车最大负载量 Maxload ,别离运用两种算法进行了查验,寻觅到的最优途径长度如表2所示。
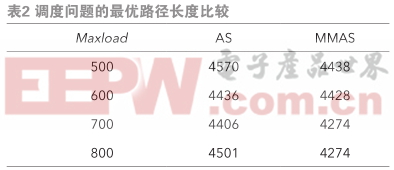
可见,最大最小蚁群算法(MMAS)往往可以得到比根本蚁群算法(AS)更优的解;此外,卡车最大负载量Maxload 也会在必定程度上影响到最优调度途径。
4 定论
本文针对一种新式物联网医疗箱体系,提出了一套运用机器学习和蚁群算法的药物调度办法,运用岭回归、随机森林回归和神经网络的混合算法树立了药品需求量的猜测模型,并运用根本蚁群算法和最大最小蚁群算法对药品的调度问题进行了求解。该办法为物联网医疗箱体系供给了一种有用的处理计划,简化了日常运营保护的进程。此外,在其他的调度问题中,该办法也供给了一种可参阅的处理思路。
称谢
最终感谢上海大学机电工程与主动化学院“挑战杯”大学生课外学术科技著作比赛项目对本文的研讨所供给的支撑。以及上海大学“罗姆杯”大学生机电工程立异规划大赛对本文研讨的支撑。
参阅文献:
[1] 赵安琪.主动售药机破冰之路[J].我国药店,2010(10):32-32.
[2] 陈雷毅,潘荣,许强,等.高校学校主动售药机的再规划[J].群众文艺,2016(11).
[3] Zhao G, Luo W, Sun R, et al. A Modified Max-Min Ant System for Vehicle RoutingProblems[C]// International Conference on Wireless Communications. IEEE, 2008.
[4]段海边.蚁群算法原理及其使用[M]. 北京 科学出版社,2005.
[5] Stützle T,Hoos H H.MAX–MIN ant system[J]. Future generation computer systems, 2000,16(8): 889-914.
[6] 陈昌敏,谢维成,范颂颂.自适应和最大最小蚁群算法的物流车辆途径优化比较[J].西华大学学报(自然科学版),2011,30(3).
[7] 李勇,段正澄.动态蚁群算法求解TSP问题[J].核算机工程与使用,2003,39(17):103-106.
[8] 柴宝杰,刘大为.依据粒子群优化的蚁群算法在TSP中的使用[J].核算机仿真,2009,26(8):89-91.
[9] Peter Harrington. Machine learning in action [M].2013.
[10] Liaw A, Wiener M. Classification and regression by randomForest[J].R news,2002,2(3):18-22.
[11] Bose N K, Liang P.Neural Network Fundamentals with Graphs,Algorithms,and Applications(McGraw-Hill Series in Electrical Computer Engineering)[J].1996.
[12] Balkić Z, Šoštarić D, Horvat G. GeoHash and UUID identifier for multi-agent systems[C]//KES International Symposium on Agent and Multi-Agent Systems: Technologies andApplications. Springer, Berlin, Heidelberg, 2012: 290-298.
[13] Cassel M, Lima F.Evaluating one-hot encoding finite state machines for SEU reliabilityin SRAM-based FPGAs[C]//On-Line Testing Symposium, 2006. IOLTS 2006. 12th IEEEInternational. IEEE, 2006: 6 pp.
作者简介:
通讯作者:李晋,男,上海大学机电工程学院试验师,硕士,首要从事微控制器技能,人工智能算法使用优化。
榜首作者:卢嘉轩,男,上海大学核算机学院本科生,首要从事人工智能算法研讨。
第三作者:周延,男,上海大学核算机学院本科生,首要从事人工智能算法研讨。
本文来源于科技期刊《电子产品世界》2019年第7期第80页,欢迎您写论文时引证,并注明出处