第一章 序言
1.1 导言
核算机断层摄像技能CT(Computerized Tomography)是20世纪医学的严重效果之一，该效果将核算机使用于医学范畴，使医学射线学发生了革命性的改动。自从CT面世以来，核算机科学与生物医学工程相结合，构成了核算机医学图画研讨的新范畴，并为生命科学的研讨供给了新的办法，成为近年来国际科技界最活泼、最富有活力和成果的范畴之一。
医学影像学将数字图画处理技能和核算机图形学技能广泛的使用于生物医学范畴中，经过把人体的内部结构以图画或图形的办法显现出来，进步了医疗确诊的可靠性，使医治能够准确和完全。
1.2 医用CT的简介
CT是核算机X射线断层造影术(Computerized Tomography)的简写。CT的创造是20世纪后期最严重的科技效果之一，由Hounsfield于1969年规划成功，1972年公诸于世。
CT运用人体各种安排(包含正常和反常安排)对X射线的吸收不等这一特性，将人体某一选定层面分红许多立方体小块(这些立方体小块称为体素)，X射线经过人体测得每一体素的密度或灰度，即为CT图画上的基本单位，称为像素。它们摆放成队伍方阵，构成图画矩阵。当X射线球管从一方向宣布X射束穿过选定层面时，沿该方向摆放的各体素均在必定程度上吸收一部分X射线，使X射线衰减。当该X射线束穿透安排层面(包含许多体素)为对面探测器接纳时X射线量已衰减许多，为该方向一切体素X射线衰减值的总和。然后X射线球管滚动必定视点，再沿另一方向宣布X射线束，则在其对面的探测器可测得沿第2次照耀方向一切体素X射线衰减值的总和;以相同办法重复屡次在不同方向对安排的选定层面进行X射线扫描，即可得到若干个X射线衰减值总和。在上述进程中，每扫描一次，即可得一方程。该方程中X射线衰减总量为已知值，而构成该总量的各体素X射线衰减值是不知道值。经过若干次扫描，即可得一联立方程组，经过核算机运算可解出这一联立方程组，而求出每一体素的X射衰减值，再经模/数转化，使各体素不同的衰减值构成相应各像素的不同灰度，各像素所构成的矩阵图画即为该层面不同密度安排的灰度图画。
螺旋CT查看包含两方面的基本内容：一是X射管及探测器接连360°旋转;二是患者一起随查看床匀速推动，如图1.2所示。在扫描时刻内，X射线焦点对患者作螺旋式运动，并一起搜集这一规模的悉数扫描数据，用线性内插法重建图画。
如图1.3所示，医用X-CT机的体系结构主要由六大部分组成，其各部分的效果如下：
(1)X射线源：发生用来检测被测物的X射线，X射线源包含X射线球管源(能量在450kV以下)和直线加速器(能量在2MeV以上)。射线源的能量，决议了穿透才能。
(2)探测体系：包含准直器、传感器、信号处理和信号传输等部分，是获取信号的要害部分，也是决议CT功能的要害部分之一。穿过被测物的X射线首要经过准直器准直并离散化，传感器先将射线转化成电信号，信号处理电路再将不规则的信号转化成规范的信号传输到核算机接口。
(3)核算机收集体系：主要由特别的专用的多信道数据收集接口电路和核算机软硬件组成。完结数据收集、转化、校对、处理等。将收集的数据处理成规范的文件格局，供图画重建、处理运用。
(4)机械扫描体系：作为各部分的载体并供给CT扫描所需的多个自由度的高精度运动。
(5)自动操控体系：包含检测、驱动、操控器(核算机)，完结扫描运动操控、体系逻辑和程控、状况监控和安全维护，和谐整机作业，并完结体系自检与数据确诊。
(6)图画处理体系：包含图画处理核算机硬件和软件，如用于图画重建与处理的高速核算机、大屏幕图画显现器、大容量数据存贮器、图画复制输出设备(打印机)、体系软件及专用软件。完结数据校对、图画重建、处理、剖析、丈量、图画输出、存贮、显现等。
咱们所研讨的CT图画重建部分处于图画处理体系中，是整个体系的瓶颈地点，也是决议体系整个进程所耗费时刻的要害部分。
1.3 CT图画重建技能概述
1.3.1 CT图画重建的简介
咱们企图重建的物体可被看作是某种函数的二维散布。关于CT，该函数代表物体线性衰减系数。关于断层重建问题的描绘，咱们能够假定收集了一组丈量成果，每个丈量成果代表沿着特定的射线途径，物体衰减系数的累加或线积分。这些丈量成果是在不同视点和到旋转中心的不同间隔上获取的。为防止数据采样的冗余，咱们假定丈量按以下次第进行。首要沿着互相平行且等距离的途径进行一组丈量。这些丈量成果构成一次“观测”或一组“投影”。在稍微改动的视点下重复相同的丈量。继续该进程直到掩盖整个360°(理论上仅有180°平行投影是必要的)。在整个进程中，相邻两次观测之间的视点增量坚持不变，并且被扫描物体在同一方位固定不动。CT重建的问题便是，咱们怎么依据这些丈量成果来估量被扫描物体的衰减系数散布。
CT图画重建问题是一个风趣而杂乱的课题。它的公示表达能够追溯到1917年，其时Radon(雷登)[2]首要找到了从函数线积分重建该函数的求解办法。跟着20世纪70年代后期和80年代前期临床有用CT扫描机的开展，该范畴的研讨活动有了极大的开展。许多研讨论文、会议论文汇编、书本章节，乃至教科书都重视这个课题[3,4]。提出了许多技能，它们在核算杂乱性、空间分辨率、时刻分辨率、噪声、临床医治计划、灵活性以及伪像各方面具有不同的折中平衡。
1.3.2 Radon(雷登)改换
CT的基本思想源于1917年奥地利数学家Radon提出的Radon改换。
Radon改换的内容能够表述为：若已知某函数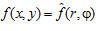
，
如图1.4所示，其沿直线S的线积分为：
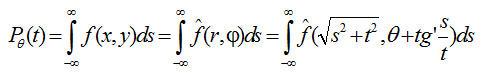
(1.1)
则
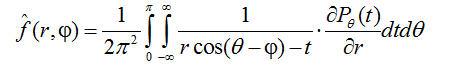
(1.2)
式(1.1)为Radon改换，实践上便是物体的投影，式(1.2)为Radon反改换，即依据投影数据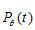 
重建函数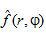 
。
1.3.3 傅里叶切片定理
傅里叶切片定理的意义是：平行投影的一维傅里叶改换等同于原始物体的二维傅里叶改换的一个切片。便是指出线性衰减系数函数f(x,y)在某一方向上的投影函数gθ(R)的一维傅立叶改换函数Gθ(ρ)是f(x,y)的二维傅立叶改换函数F(u,v)或F(ρ,θ)(极坐标方式)在(ρ,θ)平面上沿同一方向且过原点的直线上的值，如图1.5所示。
为此，咱们在不同的视点下获得足够多的投影函数数据，并作它们的傅立叶改换，那么改换后的数据就将充溢整个(u,v)平面。一旦频域函数F(u,v)或F(ρ,θ)的悉数值得到后，将其作一次傅立叶反改换，就得到原始的衰减系数函数f(x,y),即
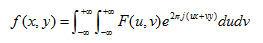
(1.3)
令u=ρcosθ，v=ρsinθ，则式(1)可进一步变形为
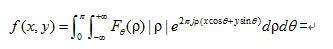
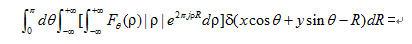
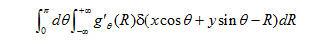
(1.4)
式中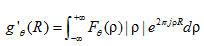 
，表明对投影函数 
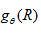的傅里叶改换函数进行滤波改换，其间 
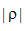为滤波函数。
由傅立叶改换性质可知，频域中的滤波运算可等效地在空域顶用卷积运算来完结，因此由(2)可得到
(1.5)
式中h(R)为滤波函数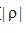 
的空域方式， 
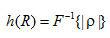，因此这种办法也称为卷积反投影办法。
运用中心切片定理[5]及二维FFT反改换法重建图画，因为勿须反投影运算,因此速度快,但图画重建进程中,需求内插运算，因此重建图画精度相对较低。
首要求出各投影数据的一维傅里叶改换，在不同的投影视点下所到的一维改换函数可构成完好的二维傅里叶改换函数，将此二维函数作一次反傅里叶改换，就得到重建图画。为了在二维逆改换中选用快速傅里叶改换算法，通常在逆改换前要将极坐标转化为直角坐标的方式。
傅里叶改换法重建法的特点是改换速度快，但精度不如滤波反投影法。算法的要害是将弧形的的极坐标数据转化成直角坐标数据时，因为在边际区高频数据削减，因此形成差错，但傅里叶改换重建法重建速度比滤波反投影可进步2-3倍一在弧形极坐标数据向直角坐标系转化时，最简略的是最附近内插法，当然这种办法精度最低，双线性内插重建图画精度好于最附近内插法，并且核算又不杂乱。
处理的办法是扩展核算区域，经过外延数据附加上一些分外的点，即核算更多的像素点以减小边际的差错。如重建图画为M×M，则可核算3M×3M区域内的FFT改换，当然这是以增加了核算量为价值的。傅里叶改换重建图画算法在内插网格点上进行一些恰当的挑选。如使径向点取在直角坐标网格的线上，这样只需一次内插，而重建图画精度有了较大的改善。
1.3.4 CT图画重建的几种算法
在实践重建傍边所存在的问题是，尽管Radon给出了一个数学公式，可是咱们需求一个有用的算法来处理它，图画重建的算法有许多，大致分为三类：准确算法、近似算法和迭代算法。近似算法中，以滤波反投影算法(Filter back projection，FBP)最具代表性，使用最为广泛。选代算法中，代数重建算法(Algebraic reconstruction technique，ART)是提出最早并最为人们了解的算法。迭代型算法(如代数重建算法等)具有许多长处，但因为核算量大、重建时刻长.在很长一段时刻内约束了其在医学和工业CT范畴的使用。进步迭代型算法的核算速度一直是人们重视的问题。近年来人们提出了不少进步迭代算核算速度的办法，加上近年来核算机核算速度的敏捷进步，迭代算法从头遭到人们喜爱。此外，因为使用的需求，部分重建算法(Local Reconstruction Algorithm， LocalRA)也在近十年中有了较大的开展。在传统大局CT算法中，即便重建物体断面中一个小区域的图画，也得环绕整个断面收集投影数据。而部分重建算法，仅需环绕感兴趣区域及其邻域收集投影数据，即可重建感兴趣区域的图画。部分重建算法可削减数据收集时刻和重建时刻，下降人体(或生物体)的放射摄入量。
