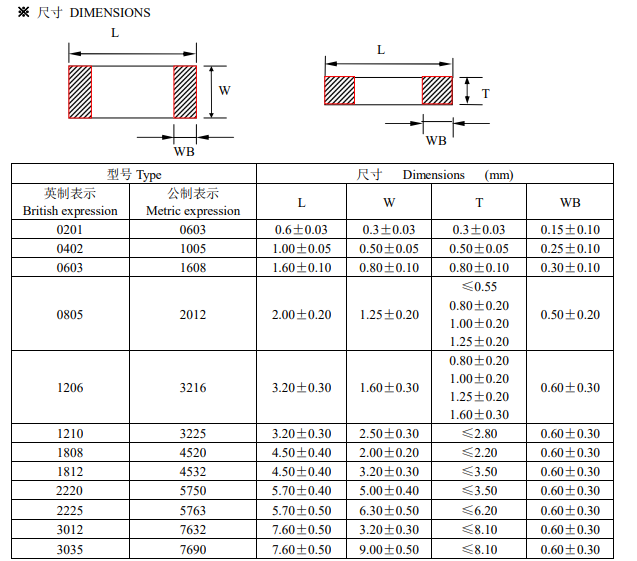
迟滞比较器又可理解为加正反应的单限比较器。 单限比较器,假如输入信号Uin在门限值邻近有细小的搅扰,则输出电压就会发生相应的颤动(崎岖)。在电路中引进正反应能够战胜这一缺陷。
图1a给出了一个迟滞比较器,人们所了解的“史密特”电路便是有迟滞的比较器。图1b为迟滞比较器的传输特性。
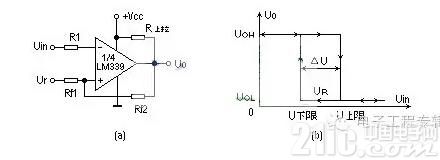
不难看出,当输出状况一旦转化后,只要在跳变电压值邻近的搅扰不超越ΔU之值,输出电压的值就将是安稳的。但随之而来的是分辩率下降。因为对迟滞比较器来说,它不能分辩不同小于ΔU的两个输入电压值。迟滞比较器加有正反应能够加速比较器的响应速度,这是它的一个长处。除此之外,因为迟滞比较器加的正反应很强,远比电路中的寄生耦合强得多,故迟滞比较器还可革除因为电路寄生耦合而发生的自激振荡。
迟滞比较器
迟滞比较器的输出VO与输入VI不成线性关系,输出电压的转化临界条件是
门限电压VP(同相输入端的电压)≈VN(反相输入端的电压)=VI(参阅基准电压)
VP=VN=[(R1×VREF)/(R1+R2)]+[(R2×VO)/(R1+R2)] (公式-1)
依据输出电压VO的不同值(VOH或VOL)能够别离求出上门限电压VT+和下门限电压VT-别离为:
VT+={[1+(R1/R2)]×VREF}-[(R1/R2)×VOL] (公式-2)
VT-={[1+(R1/R2)]×VREF}-[(R1/R2)×VOH] (公式-3)
那么门限宽度为:
ΔVT=(R1/R2)×(VOH-VOL) (公式-4)
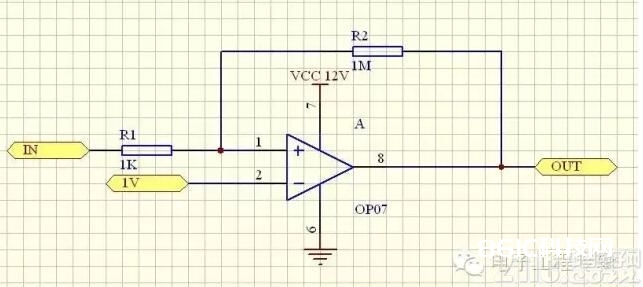
已知
作业电压=12V
基准电压VREF=1V
输入电压VI=1~5V
R1=1000Ω=1KΩ
R2=1000000Ω=1MΩ
反应系数=R1/(R1+R2)=0.000999
比较器输出电压VOH=12V, VOL=0V
而比较器的门限宽度/输出电压=反应系数
即反应系数×输出电压=门限宽度
0.000999×12=0.011988≈0.012V
依据(公式-2)VT+={[1+(R1/R2)]×VREF}-[(R1/R2)×VOL]
={[1+(1000/1000000)]×1}-[(1000/1000000)×0]
=1.001-0
=1.001(V)
依据(公式3)VT-={[1+(R1/R2)]×VREF}-[(R1/R2)×VOH]
={[1+(1000/1000000)]×1}-[(1000/1000000)×12]
=1.001-0.012
=0.989(V)
依据(公式-4)ΔVT=(R1/R2)×(VOH-VOL)
=(1000/1000000)×12
=0.012(V)
验证
VT+-VT- =1.001-0.989=0.012(V)
能够经过改动R2到达改动反应系数来调理ΔVT的规模。
例如将R2改为10KΩ时,则
ΔVT=(R1/R2)×(VOH-VOL)
=(1000/10000)×12
=1.2(V)
例如将R2改为100KΩ时,则 ΔVT=(R1/R2)×(VOH-VOL)
=(1000/100000)×12
=0.12(V)