电阻器的固有噪声,是指其本身发生的噪声,包含热噪声和过剩噪声。
热噪声
电阻器的热噪声电压能够表明为:

R是电阻,T是绝对温度,B是频率带宽,k是玻尔兹曼常数。在必定的温度和阻值之下,就发生了热噪声。
热噪声归于电阻器的本征噪声,无法防止也无法消除。
电阻的戴维宁噪声模型由噪声电压源和纯电阻构成,如图1所示。
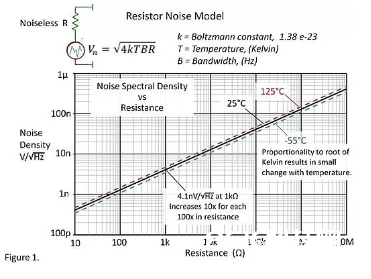
噪声电压巨细与电阻阻值,带宽和温度(开尔文)的平方根成比例联系。咱们通常会量化其每1Hz带宽内的噪声,也便是其频谱密度。电阻噪声在理论上是一种“白噪声”,即噪声巨细在带宽内是平等的,在每个相同带宽内的噪声都是相同的。
总噪声等于每个噪声的平方和再开平方。咱们常常说到的频谱密度的单位是 V/root-Hz 。关于1Hz带宽,这个数值就等于噪声巨细。关于白噪声,频谱密度与带宽开方后的数值相乘,能够计算出带宽内总白噪声的巨细。为了丈量和量化总噪声,需求约束带宽。假如不知道截止频率,就不知道应该积分到多宽的频带。
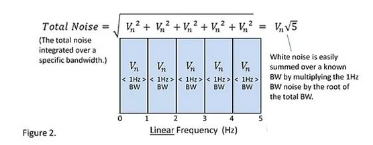
咱们都知道频谱图是以频率的对数为x轴的伯德图。在伯德图上,相同宽度右侧的带宽比左边要大得多。从总噪声来看,伯德图的右侧或许比左边更重要。
电阻噪声遵守高斯散布,高斯散布是描绘振幅散布的概率密度函数。遵守高斯散布是由于电阻噪声是由很多的小的随机事情发生的。中心极限定理解说了它是怎么构成高斯散布的。沟通噪声的均方根电压幅值等于高斯散布在±1σ范围内散布的振幅。关于均方根电压为1V的噪声,瞬时电压在±1V范围内的概率为68% (±1σ) 。人们常常以为白噪声和高斯散布之间有某种相关,事实上它们没有相关。比方,滤波电阻的噪声,不是白噪声但仍然遵守高斯散布。二进制噪声不遵守高斯散布,但却是白噪声。电阻噪声既是白噪声也一起遵守高斯散布。

纯理论研究者会以为高斯噪声并没有界说峰峰值,而它是无量的。这是对的,高斯散布曲线两边是无限扩展的,因而任何电压峰值都是有或许的。实践中,很少有电压尖峰超越±3倍的均方根电压值。许多人用6倍的均方根电压值来近似峰峰值的巨细。为了留有满足的裕度,乃至能够用8倍的均方根电压值来近似峰峰值的巨细。
一个风趣的问题是,两个电阻串联的噪声之和等于这两个电阻和的噪声。类似的,两个电阻并联的噪声之和等于这两个电阻并联后电阻的噪声。假如不是这样,那么在串联或许并联电阻时就会出问题。还好它确实是这样的。
一个高阻值电阻不会由于本身噪声电压而发生电弧和火花。电阻的寄生电容并联在电阻两头,将约束其带宽和端电压。类似的,你能够幻想绝缘体上发生的高噪声电压也会被其寄生%&&&&&%和周围的导体分流。
过剩噪声
实践电阻的固有噪声往往远大于热噪声,超越热噪声起伏的噪声称为过剩噪声。与热噪声不同,过剩噪声来源于电阻内部结构不接连性和非完整性,与电阻类型有非常大的联系。
线绕电阻内部为体金属,不接连性很小,是过剩噪声最小的电阻;
组成资料的电阻内部结构不接连,是过剩噪声最大电阻;
固有噪声:线绕 优于 金属氧化膜 优于 金属膜 优于 碳膜 优于 玻璃釉 优于 组成膜 优于 组成实心