单片机首要作用是操控外围的器材,并完成必定的通讯和数据处理。但在某些特定场合,不可避免地要用到数学运算,虽然单片机并不拿手完成算法和进行杂乱的运算。下面首要是介绍如何用单片机完成数字滤波。

在单片机进行数据收集时,会遇到数据的随机差错,随机差错是由随机搅扰引起的,其特点是在相同条件下丈量同一量时,其巨细和符号会现无规则的改动而无法猜测,但屡次丈量的成果契合核算规则。为战胜随机搅扰引起的差错,硬件上可选用滤波技能,软件上可选用软件算法完成数字滤波。滤波算法往往是体系测控算法的一个重要组成部分,实时性很强。
选用数字滤波算法战胜随机搅扰的差错具有以下长处:
l 数字滤波无需其他的硬件本钱,只用一个核算进程,可靠性高,不存在阻抗匹配问题。尤其是数字滤波能够对频率很低的信号进行滤波,这是模仿滤波器做不到的。
l 数字滤波运用软件算法完成,多输入通道可共用一个滤波程序,下降体系开支。
l 只需恰当改动滤波器的滤波程序或运算,就能便利地改动其滤波特性,这关于滤除低频搅扰和随机信号会有较大的作用。
l 在单片机体系中常用的滤波算法有限幅滤波法、中值滤波法、算术均匀滤波法、加权均匀滤波法、滑动均匀滤波等。
(1)限幅滤波算法
该运算的进程中将两次相邻的采样相减,求出其增量,然后将增量的绝对值,与两次采样答应的最大差值A进行比较。A的巨细由被测目标的具体情况而定,假如小于或等于答应的最大差值,则本次采样有用;否则取前次采样值作为本次数据的样本。
算法的程序代码如下:
#define A //答应的最大差值
char data; //上一次的数据
char filter()
{
char datanew; //新数据变量
datanew=get_data(); //取得新数据变量
if( (datanew-data)》A||(data-datanew》A) )
return data;
else
return datanew;
}
阐明:限幅滤波法首要用于处理改动较为缓慢的数据,如温度、物体的方位等。运用时,要害要选取适宜的门约束A。一般这可由经历数据取得,必要时可通过试验得到。
(2)中值滤波算法
该运算的进程是对某一参数接连采样N次(N一般为奇数),然后把N次采样的值按从小到大摆放,再取中心值作为本次采样值,整个进程实际上是一个序列排序的进程。
算法的程序代码如下:
#define N 11 //界说取得的数据个数
char filter()
{
char value_buff[N]; //界说存储数据的数组
char count,i,j,temp;
for(count=0;count《N;count++) //获取数据
{
value_buf[count]=get_data();
delay(); //假如收集数据比较慢,那么就需要延时或中止
}
for(j=0;j《N-1;j++) //用冒泡法对数据进行排序,当然最好用其他排序办法
{
for(value_buff[i]》value_buff[i+1]
{
temp=value_buff[i];
value_buff[i]=value_buff[i+1];
value_buff[i+1]=temp;
}
}
return value_buff[(N-1)/2];
}
阐明:中值滤波比较适用于去掉由偶尔要素引起的动摇和采样器不稳定而引起的脉动搅扰。若被丈量值改动比较慢,选用中值滤波法作用会比较好,但假如数据改动比较快,则不宜选用此办法。
(3)算术均匀滤波算法
该算法的基本原理很简单,便是接连取N次采样值后进行算术均匀。
算法的程序代码如下:
char filter()
{
int sum=0;
for (count=0;count《N;count++)
{
sum+=get_data();
delay():
}
return (char)(sum/N);
}
阐明:算术均匀滤波算法适用于对具有随机搅扰的信号进行滤波。这种信号的特点是有一个均匀值,信号在某一数值邻近上下动摇。信号的均匀滑润程度完全到决于N值。当N较大时,滑润度高,灵敏度低;当N较小时,滑润度低,但灵敏度高。为了便利求均匀值,N一般取4、8、16、32之类的2的整数幂,以便在程序顶用移位操作来替代除法。
(4)加权均匀滤波算法
因为前面所说的“算术均匀滤波算法”存在滑润度和灵敏度之间的对立。为了和谐滑润度和灵敏度之间的联系,可选用加权均匀滤波。它的原理是对接连N次采样值别离乘上不同的加权系数之后再求累加,加权系数一般先小后大,以杰出后边若干采样的作用,加强体系对参数改动趋势的知道。各个加权系数均小于1的小数,且满意总和等于1的完毕条件。这样加权运算之后的累加和即为有用采样值。其间加权均匀数字滤波的数学模型是:
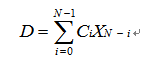
式中:D为N个采样值的加权均匀值:XN-i为第N-i次采样值;N为采样次数;Ci为加权系数。加权系数Ci表现了各种采样值在均匀值中所占的份额。一般来说采样次数越靠后,取的份额越大,这样可增加新采样在均匀值中所占的比重。加权均匀值滤波法可杰出一部分信号抵抗另一部分信号,以进步采样值改动的灵敏度。
样例程序代码如下:
char code jq[N]={1,2,3,4,5,6,7,8,9,10,11,12}; //code数组为加权系数表,存在程序存储区
char code sum_jq=1+2+3+4+5+6+7+8+9+10+11+12;
char filter()
{
char count;
char value_buff[N];
int sum=0;
for(count=0;count《N;count++)
{
value_buff[count]=get_data();
delay();
}
for(count=0;count《N;count++)
sum+=value_buff[count]*jq[count];
return (char)(sum/sum_jq);
}
(5)滑动均匀滤波算法
以上介绍和各种均匀滤波算法有一个共同点,即每获取一个有用采样值有必要接连进行若干次采样,当采速度慢时,体系的实时得不到确保。这儿介绍的滑动均匀滤波算法只采样一次,将一次采样值和曩昔的若干次采样值一同求均匀,得到的有用采样值即可投入运用。假如取N个采样值求均匀,存储区中有必要拓荒N个数据的暂存区。每新收集一个数据便存入暂存区中,一起去掉一个最老数据,保存这N个数据始终是最新更新的数据。选用环型行列结构能够便利地完成这种数据寄存方法。
程序代码如下:
char value_buff[N];
char i=0;
char filter()
{
char count;
int sum=0;
value_buff[i++]=get_data();
if(i==N)
i=0;
for(count=0;count《N;count++)
sum=value_buff[count];
return (char)(sum/N);
}
今日就写到这,因为数字滤波的算法还有许多种办法,比方一阶滞后低通滤波器(惯性滤波法),限时滤波,容错冗余三中取二滤波法等等。不过因为个人能力和时刻的原因,还没能把它们一一地列出。今后我会不断地找材料把它们完善。