无刷直流电机的操控是依据转子磁极方位向电枢通以电流来完成的,然后需求依托旋转编码盘或许其他传感器来检测转子的方位。跟着小型化,低成本和可靠性的趋势,要求无刷直流电机(BLDC)的驱动选用无方位传感器的需求越来越大。的确有一些这类的办法[1,2],可是很少有办法能有用处理磁路的非线性,电机参数的动摇和其他问题。
关于感应电机,一些运用了神经网络的驱动办法曾被提出[3,4]。另一方面,至于BLDCM,也有一些在仿真阶段的研讨[5,6],但他们的有用性还没被实在的电机试验证明过。
在这项研讨中,咱们提出和评价了一种运用神经网络(NN)的无方位传感器的驱动办法,特别的,他们描绘非线性体系和一般化的才能是通过练习得到的。在第二章,解说了BLDCM的运转原理和无方位传感器驱动的概念。在第三章,咱们提出了依据神经网络的无方位传感器驱动办法,考虑了它的练习。第四章给出了试验的成果。咱们展现提出的办法不只具有杰出的速度特性,其电压和电流小型也是适宜的。在第五章,咱们证明了通过参数动摇的比如证明了NN的可能性。在结束,咱们给出了定论和往后研讨的主题。
2 无方位传感器驱动
2.1 BLDCM模型
假定一个圆型的永磁感应电机被当作一个BLDCM,其转子磁场呈正弦散布。顺时针旋转被以为正方向。在这种情况下,在d-q坐标下的旋转方程如下[3]
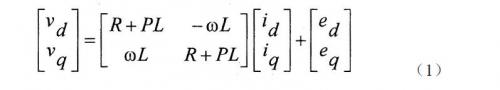
在这儿,vd和vq分别为d-和q-轴电枢电压重量,id和iq为d-和q-轴电枢电流重量,ed和eq为d-和q-轴由电枢电流通过永久磁场感应的电动势,P为微分运算符。因而,

因为d轴在d-q坐标下与磁体系发生的磁通方向共同,d-q坐标旋转速度和磁体系的旋转速度相同。因而,电压、电流和其它参数在d,q轴能够被当作直流量来看待。
电机扭矩在d-q轴上表明如下:

这儿p代表极对数。
在公式(3)里边,KE受磁体温度的和饱满的影响,但不会发生太大改动。这样,电机扭矩能够通过iq操控。通过坚持id=0能够完成最好的效果,因而撤销与id相关的丢失带来的影响。
2.2 无方位传感器操控
当无方位操控运用在BLDCM时,d-q轴的方位不确定,因而选用虚轴 上的方位和速度来替代,如图1所示。 一种估量这些量的办法描绘如下。
首要,在d-q轴上旋转方程(1) 转化状态方程如下:
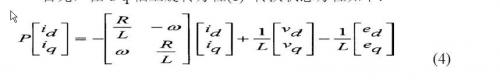
然后转化在轴上进行。该改换矩阵[c]是运用旋转发生的方位差得到的,如图1所示

将该转化矩阵运用于公式(4),在轴上得到如下状态方程:
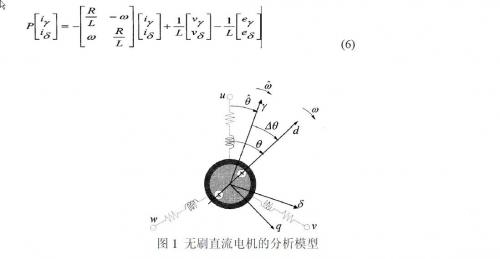
图1 无刷直流电机的剖析模型
这儿和为-和-轴电枢电压,和为-和-轴电枢电流,和为-和-轴电枢电流在永磁体中的感应电动势,而且

对公式(6)中的电流差分项运用欧拉近似,而且假定电枢电压 和 在采样期间为稳定,则关于采样周期T,在采样点n-1和n,能够用下面的离散状态方程描绘:
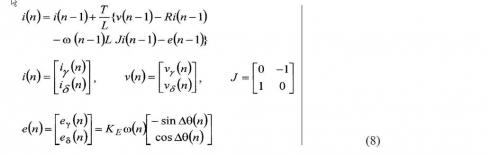
因而,在 轴上的电动势e(n)包括了相位差错和速度信息。因而在 坐标上的方位和速度通过预算 坐标上的电动势和运用与相位差错和速度有关的信息,能被融合到d-q轴上的方位和速度。
一种预算 坐标上电动势e(n)的办法能够通过改换公式(8)得到,如下:
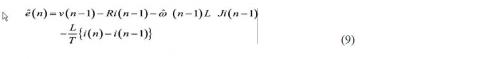
当得到电动势的估量值 后,用速度估量值 来替代不知道速度 。用电动势的估量式(9)和方位差错估量值 以及速度 能够由下式得到:

运用公式(10)、(11),咱们能够得到实在方位 (在d-q坐标)来批改 坐标下的方位 ,如下:

这儿,K为渐近收敛的 的方位差错批改系数
。
相似的,收敛的实在速度 (在d-q坐标下)能够通过批改 坐标下的速度 得到,如下:

因而,实在的方位和速度能够通过估量 坐标下的电动势得到。事实上,但是,电机内部的磁路因为永磁体和和其他要素的影响对错线性的。这样,咱们能够假定理论的估量包括了差错。此外,实践的电机参数也跟着温度和其他条件而动摇。咱们测验通过引进神经网络来处理这种估量差错,这种神经网络能够描绘非线性体系和具有学习才能。无刷直流电机的无传感器操控是通过选用神经网络估量的电机的方位和速度来进行的。
3 运用神经网络的无方位传感器驱动
3.1 通过神经网络估量方位和速度
通过神经网络来考虑电动势的估量。咱们通过引进下面的多变量的函数g,在 坐标下对电动势归纳方程(9),该函数包括电流i(n),i(n-1),电压v(n-1),和估量速度 :
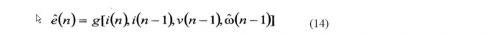
咱们提出一种通过神经网络来表明多变量函数和办法,这种办法被当作电动势估量的神经网络模型。速度和方位由(10)-(13)式核算。
至于神经网络的练习数据,最好的办法是用电机旋转的实践参数(电压,电流,速度)。因而,咱们假定练习的数据是在实践运转过程中通过传感器得到的。装有传感器的电机被驱动后,电压、电流和速度等数据就被测得。通过改动速度参阅取得的练习数据,咱们能够等待神经网络的归纳(一般化)才能有一种进步。
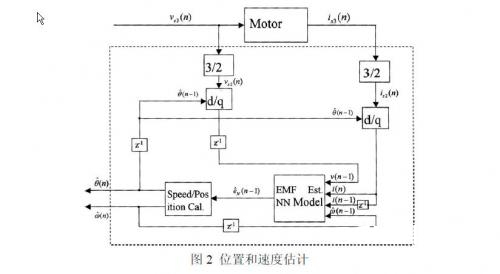
在一种神经网络练习办法中,将取的数据输入神经网络,当由(9)式估量的电动势和电动势估量的神经网络模型的输出相差满足小之前,练习的效果表现出来。通过练习后的神经网络估量的方位和速度见图2。
3.2 仿真
图2所示的方位/速度预算被归入BLDCM操控体系来得到由图3所示的整体结构。
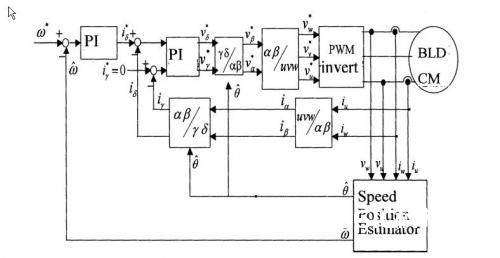
图3 无传感器驱动体系结构
在这个操控体系里边,PI操控被运用到速度和电流调理中。首要,在速度操控单元,依据参阅速度 和估量速度 的差值来完成PI操控, 轴的参阅电流 为输出,如下:

这儿Kvp和Kvi分别为速度份额系数和速度积分系数。别的, 轴参阅电流 坚持0以得到最大的功率。然后 ,在电流操控环中也运用了PI操控,以使实践的 , 和希望的参阅值附近。参阅 , 由下式得到:
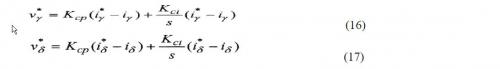
这儿Kcp和Kci分别为电流份额系数和积分系数。
运用Matlab/Simulink仿真模型结构如图3所示。在电动势估量模型中设有7个输入层,14个中间层和两个输出层。获取练习数据的意图是处理参阅速度和负载的动摇。特别地,在扭矩为0.001,0.5,1.0 N-m,当参阅速度从400→800→1200rpm,通过一个方位传感器驱动电机。由此而得到的三项练习数据单元然后被归纳,神经网络然后得到如前所述的练习。直到练习数据希望的均方差下降到3.36403×10-3,练习才履行。通过这样的离线练习后,电动势估量的神经网络模型被合并到操控体系,当扭矩从0.1以0.1N-m的步进增加到1N-m(和练习时相同)时,进行仿真。仿真成果如图4.

图4 仿真成果









