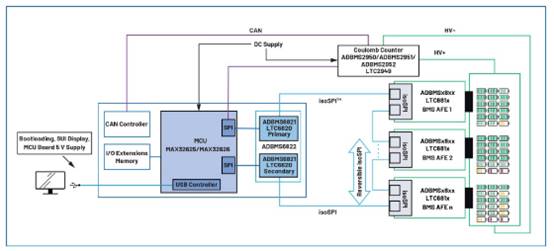
Σ-Δ型ADC是当今信号收集和处理体系规划人员的工具箱中必不可少的底子器材。本文的意图是让读者对Σ-Δ类型ADC拓扑结构背面的底子原理有一个底子了解。本文探讨了与ADC子体系规划相关的噪声、带宽、树立时刻和一切其他要害参数之间的权衡剖析示例,以便为精细数据收集电路规划人员供给布景信息。
它一般包含两个模块:Σ-Δ调制器和数字信号处理模块,后者一般是数字滤波器。Σ-Δ型ADC的扼要框图和首要概念如图1所示。
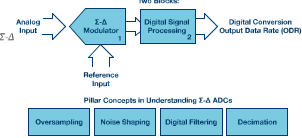
图1.Σ-Δ型ADC的要害概念。
Σ-Δ调制器是一种过采样架构,因而,咱们从奈奎斯特采样理论和计划以及过采样ADC操作开端评论。
图2比较了ADC的奈奎斯特操作、过采样计划和Σ-Δ调制(也是过采样)计划。
图2a显现了ADC以规范奈奎斯特办法运转时的量化噪声。这种情况下,量化噪声由ADC的LSB巨细决议。FS为ADC的采样速率,FS/2为奈奎斯特频率。图2b显现的是同一转化器,不过现在它以过采样办法运转,采样速率更快。采样速率进步K倍,量化噪声扩展到K × FS/2的带宽上。低通数字滤波器(一般带抽取功用)可消除蓝色区域之外的量化噪声。
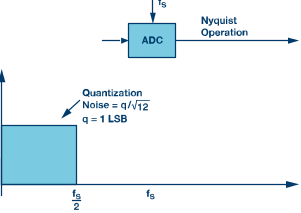
图2a.奈奎斯特计划。采样速率为FS ,奈奎斯特带宽为FS /2。
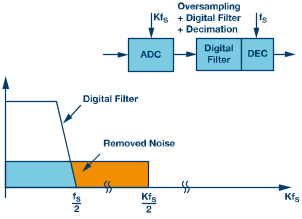
图2b.过采样计划。采样速率为K × FS。
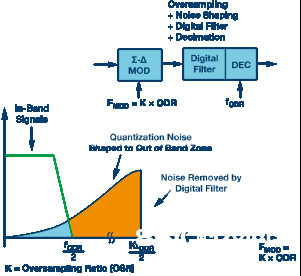
图2c.Σ-Δ型ADC计划。过采样和噪声整形,采样速率为FMOD = K × FODR。
Σ-Δ调制器多了一个特性,那便是噪声整形,如图2c所示。模数转化的量化噪声被调制整形,从低频移动到较高频率(一般如此),低通数字滤波器可将其从转化成果中消除。Σ-Δ型ADC的噪底由热噪声决议,而不受量化噪声的约束。
采样、调制、滤波
Σ-Δ型ADC运用内部或外部采样时钟。ADC的主时钟(MCLK)常常要先分频,再交由调制器运用;阅览ADC数据手册时应留意这点,并了解调制器频率。传送到调制器的时钟设置采样频率FMOD。调制器以该速率将数据输出到数字滤波器,从而数字滤波器(一般为低通,带抽取功用)以输出数据速率(ODR)供给数据。图3显现了这一进程。
一阶Σ-Δ调制器的深化调查
Σ-Δ调制器是一种负反应体系,与闭环放大器类似。环路包含低分辨率ADC和DAC,以及一个环路滤波器。输出和反应被大略量化,常常只要一比特表明高电平或低电平的输出。ADC的模仿体系完结了这种底子结构,量化器便是完结采样的模块。假如存在确保环路安稳的条件,那么输出便是输入的大略表明。数字滤波器获得该大略输出偏重构模仿输入的准确数字转化成果。
图4显现了呼应一个正弦波输入的1密度输出。调制器输出从低电平到高电平的改变率取决于输入的改变率。当正弦波输入为正满量程时,调制器输出开关速率会下降,输出以+1状况为主。相同,当正弦波输入为负满量程时,+1和–1之间的转化会削减,输出以–1为主。当正弦波输入处于最大改变率时,调制器输出产生最高密度的+1和–1切换。输出改变率与输入改变率同步。因而,模仿输入由Σ-Δ调制器输出的转化率来描绘。
若运用线性模型来描绘这种1位调制器(Mod 1),则可将该体系表明为一个带负反应的控制体系。量化噪声为量化器的输入与输出之差。输入误差节点之后是一个低通滤波器。在图5b中,量化噪声用N来表明。
H(f)是环路滤波器的函数,界说噪声和信号的传递函数。H(f)是一个低通滤波器函数,在低频(方针带宽内)时具有十分高的增益,可衰减高频信号。环路滤波器可完结为简略的积分器或积分器级联。实践中常常把一个DAC放在反应途径中,以便获取数字输出信号并将其转化为模仿信号反应到模仿输入误差节点。
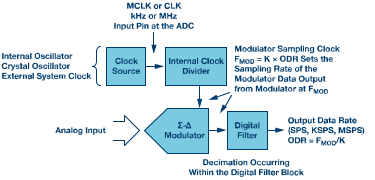
图3.Σ-Δ ADC流程:从调制器输出到数字滤波输出的采样。
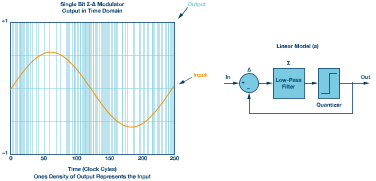
图4.输入正弦波的Σ-Δ输出1码值的密度。1阶Σ-Δ调制器环路的线性模型(a)
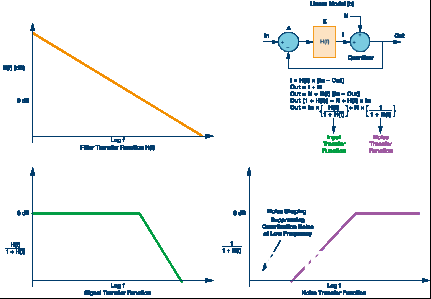
图5.Mod 1 Σ-Δ环路的线性模型(b),包含方程、滤波器、信号和噪声传递函数图。
解出图5所示方程便可得到信号和噪声传递函数。信号传递函数用作一个低通滤波器,在方针带宽内的增益为1。噪声传递函数是一个高通滤波器函数,供给噪声整形,在DC邻近的较低频率,对量化噪声有很强的按捺。在超出方针带宽的较高频率看到的量化噪声会添加。关于一阶调制器(Mod 1),噪声以大约20 dB/十倍频程的速率进步。
为了进步体系分辨率,常见办法是将两个环路滤波器级联起来以添加环路滤波器阶数。现在,总环路滤波器的H(f)具有更大的滚降,Mod 2型的噪声传递函数具有40 dB/十倍频程的上升速率。噪声所在的频率越低,噪声整形就越凶猛。图6比较了Mod 1型和Mod 2型Σ-Δ ADC。Σ-Δ调制器的改变和款式十分多。规避了高阶1位环路安稳性问题的架构称为多级噪声整形调制器(MASH)架构。多级(MASH型)架构支撑经过具有内涵安稳性的低阶环路组合来规划安稳的高阶Σ-Δ调制器。
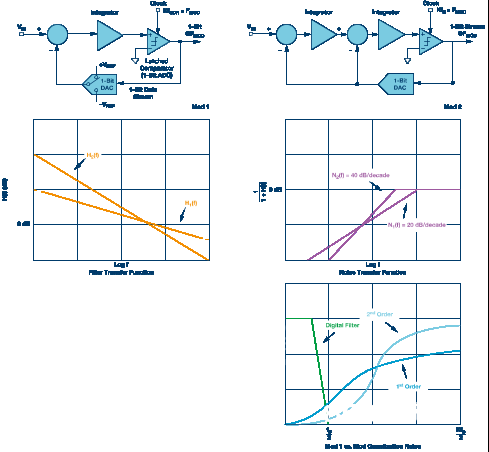
图6.Mod 1和Mod 2框图装备以及滤波器和噪声传递函数的比较图。