一、峰峰值颤动、均方根颤动
曩昔多年来用于量化颤动的最常用的办法是峰峰值颤动(Peak-to-peak Jitter)和均方根颤动(Root-Mean-Square Jitter,颤动直方图或许颤动散布的1 或许RMS值)。可是因为随机颤动以及非固定颤动的存在,使得颤动的峰峰值跟着调查样本数量的添加而添加,因而说峰峰值颤动参数用于衡量固有颤动会很有用,可是衡量随机性颤动却会呈现很大差错;相同的道理,因为固有颤动及非高斯性颤动和噪声的存在,使得颤动的直方图或许散布图不呈现彻底的高斯散布,因而计算得到的颤动的1σ或许RMS值不等于实在高斯散布的1 值。
峰峰值颤动和均方根颤动均是对某一类颤动的计算分析目标。
二、相位颤动、周期颤动、相邻周期间颤动
因为时钟体系是数字电路体系十分要害的一部分,直接决议了数据信号发送和接纳的胜败,是整个体系的主动脉,因而时钟的颤动一向备受重视。描绘时钟体系的颤动参量一般分为三类,即相位颤动(Phase jitter)、周期颤动(Period jitter)、相邻周期间颤动(Cycle to cycle jitter).
1、相位颤动
在数字体系中,两个逻辑电平之间的切换一般伴跟着快沿的呈现,这些边缘在时序上的不稳定性就叫做相位颤动(phase jitter,有时也叫累积颤动,accumulated jitter,指实践边缘方位与抱负边缘方位的误差,以时刻为单位,也能够换算成弧度,视点等);相位颤动是相位噪声在数字域的等效表现,它是离散量,因而只有当边缘存在时分才有界说。
抱负边缘方位一般界说在数字信号一个比特位时刻距离的整数倍方位处。如下图1所示为某一
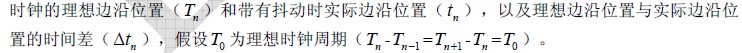



不会直接运用时钟的边缘来确保时序联系,而是看周期的稳定性,也便是周期的颤动,有时分时钟周期越长,或许带来坚持时刻余量缺乏的问题,这个时分就需求丈量周期颤动;而相邻周期间颤动常常能够用来衡量时钟分频器的稳定性。总归,这三种颤动都是衡量时钟自身功能的目标,在不同的使用布景下需求重视不同的目标,一般时钟芯片的手册会给出对时钟的颤动目标要求。