导言
在电子对抗领域中辐射源测向是一个根本问题。能发射电离辐射的物质或设备。从广义上讲，凡能开释各种电离辐射的物质或设备（如宇宙射线）均可视为辐射源。但习惯上用于γ探伤、放射医治和辐射加工等的放射性深度较高的放射源称为辐射源。干与仪测向体系的首要长处是精度高和作业频率规模宽，但现在运用的干与仪体系还存在缺乏，首要包含：（1）在被迫制导等领域中测向精度依然不行：（2）对现代雷达运用的宽带脉压信号适应能力有限；（3）有待进一步进步体系的作业频率规模。针对上述问题，本系列论文提出了数字化宽带测向体系的全体解决方案，要点评论数字化相位差丈量及差错剖析、概率解含糊算法和在测向精度和作业频率规模束缚下怎么进行天线阵列基线规划三个问题。
本文是系列论文的第一篇，给出了数字化宽带测向体系模型，评论了数字化相位差丈量办法，推导了数字化相位丈量的数字化办法差错函数和由通道噪声引起的信号相位差错散布密度函数。相位差丈量的精度直接影响体系测向的精度，还会影响解相位差含糊和天线阵列基线设置等一系列体系规划问题。传统的相位差丈量办法都是使用窄带信号干与原理把相位差转化为起伏进行丈量的，因此其只能够适用于窄带信号的相位差丈量，且丈量精度受起伏丈量差错的影响较大。本文提出的数字化相位差丈量办法，其根本思想是把信号转化到频率域，使用信号的相位谱直接完结在给定频率点上相位差的丈量，且全面的剖析了相位差丈量差错。
1 数字化宽带测向体系模型
数字化便是将许多复杂多变的信息转变为能够衡量的数字、数据，再以这些数字、数据建立起恰当的数字化模型，把它们转变为一系列二进制代码，引进核算机内部，进行一致处理，这便是数字化的根本进程。解说二：数字化将任何接连改变的输入如图像的线条或声响信号转化为一串别离的单元，在核算机顶用0和1表明。通常用模数转化器履行这个转化。当今年代是信息化年代，而信息的数字化也越来越为研究人员所注重。早在40年代，香农证明了采样定理，即在必定条件下，用离散的序列能够彻底代表一个接连函数。就本质而言，采样定理为数字化技能奠定了重要根底。英文digit译成“数字”是大陆的译法。最开端是不是由原信产部的研究所科研人员这样译出，尚不可考，愿有心有力者相助查寻。
非均匀线阵的天线数为m，天线的距离分别为d1，d2，L dm-1宽带入射信号分别为s（t），入射方向与阵列法线的交角分别为θ。
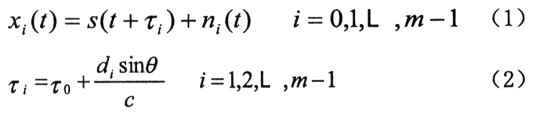
其间τ信号在第i个天线上相关于第O个天线的时间延迟，c是光速常数，di（l=1，2，L，m一1）为天线距离。对式（2）两头同做傅立叶改换：
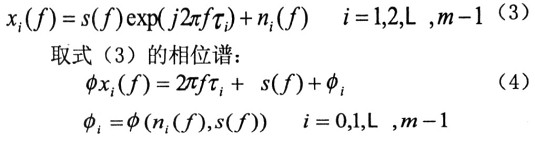
式（4）中φs（f）表明信号s的相位谱；φi为由噪声谱对信号相位谱影响发生的差错。作如下的相位差改换：
式（6）中相位差△φxi（f）是无含糊的相位差。但是实践中因为天线阵列的距离大于半波长因此相位差是有含糊的。
无妨令：
式中bi是有含糊的相位差，ni表明含糊整数，ai为相对基线长度，ei为相位差差错。则式（6）可代换为：
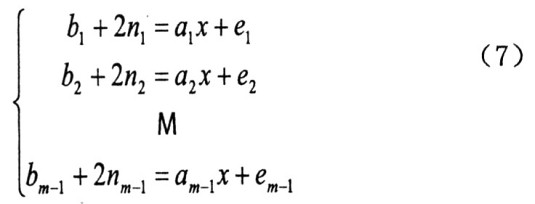
这是数字化宽带测向体系模型。
以下的作业都是环绕这个模型打开。其一是怎么丈量相位差bi（i=1，2，L，m一1） 及推导相位差丈量差错ei（i=l，2，L，m一1）的散布密度函数。其二是怎么快速求解含糊整数ni（i=1，2，L，m一1），即快速解含糊问题，这将在第二篇论文中评论。其三是怎么求解x的最优估计值然后取得测向角θ=arcsin（x），并进行测向角丈量差错剖析；一起还会评论怎么进行天线阵列的规划问题。
2 数字化相位差丈量及数字化办法差错
无妨设两个通道的时延为τ，信号为△t，信号持续时间为s（t），采样距离为N，采样点数为T。
式（14）即为相位差丈量的数字化办法差错函数。
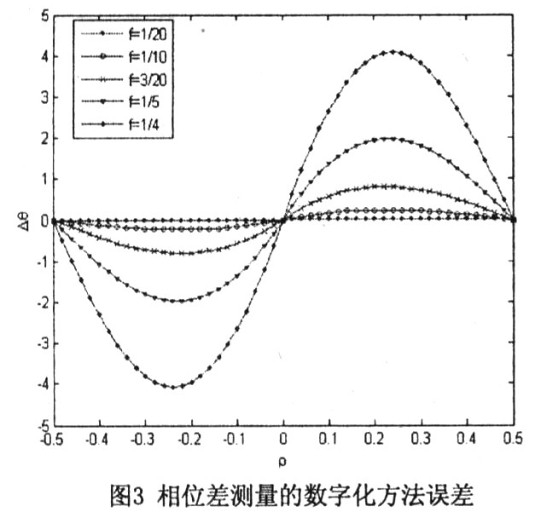
从图3中能够看出：在f=1／4，即采样频率是所测频率的4倍时，相位差最大差错约为40；当采样频率是所测频率的20倍时，办法差错能够疏忽。
3通道高斯白噪声引起的信号相位差错设通道噪声是高斯白噪声N（O，σ2），采样点数为N。则有：（1）其在离散傅立叶改换序列的实部序列和虚部序列是独立同散布的高斯白噪声序列（证明略）。（2）噪声的起伏谱遵守瑞利散布，相位谱遵守均匀散布（证明略）。（3）噪声对信号相位谱的影响。
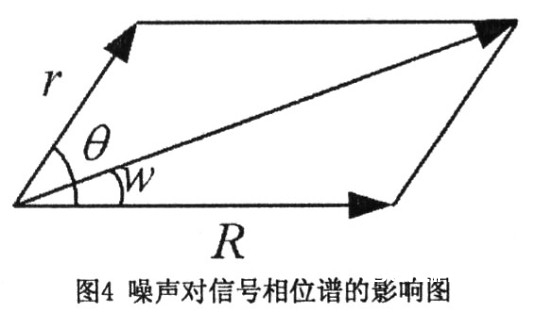
图4中，R为信号频谱起伏值，r，θ为噪声频谱起伏值和相角，w为噪声引起的信号相位差错。
令θ’=θ，则有：
设噪声的归一化带宽为B，信号的起伏一致性系数为ρ，白噪声功率为σ2，信噪比为SN，则核算噪声对信号的相位谱的影响联系。其间ρ义为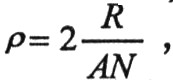
经过简略证明可得的零直流重量信号的起伏一致性系数ρ≤1。则：
式（16）即为噪声引起的相位差错散布密度函数。
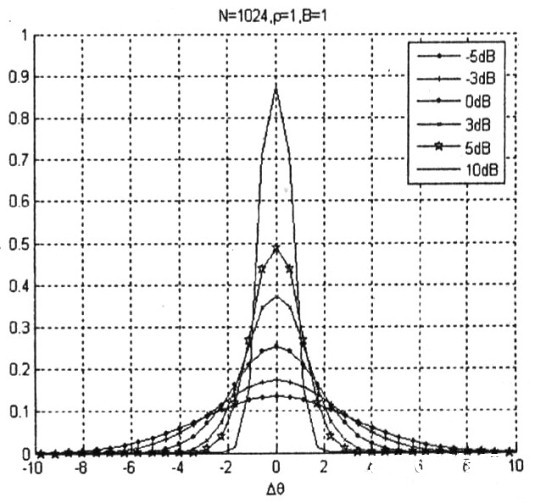
图6噪声引起的相位差错散布密度函数和信噪比的联系
图6中显现，由通道高斯白噪声引起的信号相位差错散布近似于高斯散布。
4 结束语
本文首要给出了数字化宽带测向体系模型（式（7））和数字化相位差丈量的原理公式（式（13）），推导了相位差丈量的数字化办法差错函数（式（14））和由通道高斯白噪声引起的信号相位差错散布密度函数（式（16））。
