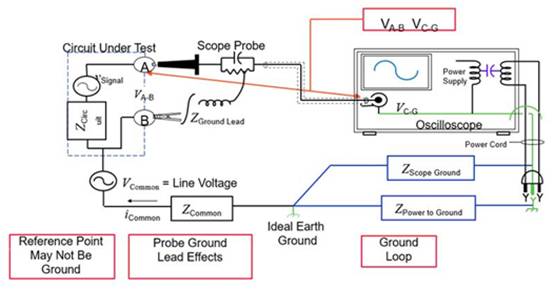
这是《小波改换和motion信号处理》系列的第一篇,根底遍及。第二篇我预备写深化小波的东西,第三篇解说运用。
记住我还在大四的时分,在请求出国和保研中犹疑了好一阵,骨子里的保存最终让我选择了先保研。当然后来也退学了,不过这是后话。其时保研就要找老板,实验室,自己命运还不错,进了一个在本校很牛逼的实验室干生路。咱们实验室主要是搞图画的,实力在全国也是很强的,进去后和师兄师姐聊,咱们都在搞什么小波改换,H264之类的。其时的我心思都不在这方面,尽搞什么操作系统移植,ARM+FPGA这些东西了。对小波改换的知道也就停留在奥秘的“图画视频紧缩算法之王”上面。
后来我才发现,在其他很广泛的领域中,小波也逐步开端盛行。比方话说很早曾经,咱们触摸的信号频域处理底子都是傅立叶和拉普拉斯的全国。但这些年,小波在信号剖析中的逐步昌盛和遍及。这让人不得不感到猎奇,是什么特性让它在图象紧缩,信号处理这些要害运用中更得到信任呢?说实话,我还在国内的时分,就开端猎奇这个问题了,所以放狗搜,放毒搜,找遍了中文讲小波改换的科普文章,发现没几个讲得清楚的,其时猎奇心没那么重,也不是搞这个研讨的,懒得找英文大部头论文了,所以作罢。后来来了这边,有些项目要用信号处理,不得已触摸到一些小波改换的东西,才开端硬着头皮看。看了一些材料,听了一些课,才发现,仍是那个陈词滥调的论调:国外的技术材料和国内真TNND不是一个层次的。相同的工作,他人说得很清楚,连我这种并不聪明的人也看得懂; 国内的材料则绕来绕去讲得乌烟瘴气,除了少量天才没几个人能在短时刻把握的。
怨言就不持续发挥了。在这个系列文章里,我期望能简略介绍一下小波改换,它和傅立叶改换的比较,以及它在移动渠道做motion detection的运用。假如不做特别阐明,均以离散小波为比方。考虑到我曾经看中文材料的苦楚程度,我会尽量用简略,可是直观的方法去介绍。有些必要的公式是不能少的,但我尽量少用公式,多用图。其他,我不是一个好的翻译者,所以关于某些真实翻译不清楚的术语,我就会直接用英语。我并不claim我会把整个小波改换讲清楚,这是不可能的事,我只能极力去环绕关键打开,比方小波改换相对傅立叶改换的长处,这些长处的原因是什么,小波改换的几个底子性质是什么,背面的推导是什么。我期望到达的意图便是一个小波改换的初学者在看完这个系列之后,就能用matlab或许其他东西对信号做小波改换的底子剖析并且知道这个剖析大概是怎样回事。
最终阐明,我不是研讨信号处理的专业人士,所以文中必有遗漏或许过错,如发现还请不吝赐教。
要讲小波改换,咱们有必要了解傅立叶改换。要了解傅立叶改换,咱们先要弄清楚什么是”改换“。许多处理,不管是紧缩也好,滤波也好,图形处理也好,实质都是改换。改换的是什么东西呢?是基,也便是basis。假如你暂时有些遗忘了basis的界说,那么简略说,在线性代数里,basis是指空间里一系列线性独立的向量,而这个空间里的任何其他向量,都能够由这些个向量的线性组合来表明。那basis在改换里边啥用呢?比方说吧,傅立叶打开的实质,便是把一个空间中的信号用该空间的某个basis的线性组合表明出来,要这样表明的原因,是由于傅立叶改换的实质,是。小波改换天然也不破例的和basis有关了。再比方你用Photoshop去处理图画,里边的图画拉伸,回转,等等一系列操作,都是和basis的改动有关。
已然这些改换都是在搞基,那咱们天然就简略想到,这个basis的选取十分重要,由于basis的特色决议了详细的核算进程。一个空间中可能有许多种方法的basis,什么样的basis比较好,很大程度上取决于这个basis服务于什么运用。比方假如咱们期望选取有利于紧缩的话,那么就期望这个basis能用其间很少的向量来最大程度地表明信号,这样即便把其他向量给砍了,信号也不会丢失许多。而假如是图形处理中常见的线性改换,最省核算量的完美basis便是eigenvector basis了,由于此刻改换矩阵T对它们的效果等同于对角矩阵( Tv_n = av_n,a是eigenvalue )。总的来说,抛开详细的运用不谈,一切的basis,咱们都期望它们有一个一起的特色,那便是,简略核算,用最简略的方法出现最多的信号特性。
好,现在咱们对改换有了底子的知道,知道他们其实便是在搞基。当然,搞基也是分方法的,不同的改换,搞基的妙处各有不同。接下来先看看,傅立叶改换是在干嘛。
傅立叶级数最早是Joseph Fourier 这个人提出的,他发现,这个basis不仅仅存在与vector space,还存在于function space。这个function space实质上仍是一个linear vector space,可所以有限的,可所以无限的,只不过在这个空间里,vector便是function了,而对应的标量便是实数或许复数。在vector space里,你有vector v能够写成vector basis的线性组合,那在function space里,function f(x)也能够写成对应function basis的线性组合,也有norm。你的vector basis可所以正交的,我的function basis也可所以正交的(比方sin(t)和sin(2t))。仅有不同的是,我的function basis是无量尽的,由于我的function space的维度是无量的。好,详细来说,那便是现在咱们有一个函数,f(x)。咱们期望将它写成一些cos函数和一些sin函数的方法,像这样
again,这是一个无限循环的函数。其间的1,cosx, sinx, cos2x …..这些,便是傅立叶级数。傅立叶级数运用如此广泛的主要原因之一,便是它们这帮子function basis是正交的,这便是风趣的当地了。为什么function basis正交如此重要呢?咱们说两个vector正交,那便是他俩的内积为0。那关于function basis呢?function basis怎样求内积呢?
现在先温习一下vector正交的界说。咱们说两个vector v,w假如正交的话,应契合:
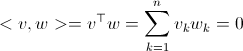
那什么是function正交呢?假定咱们有两个函数f(x)和g(x),那是什么?咱们遵从vector的思路去想,两个vector求内积,便是把他们相同方位上对应的点的乘积做一个累加。那移过来,便是对每一个x点,对应的f和g做乘积,再累加。不过问题是,f和g都是无限函数阿,x又是一个接连的值。怎样办呢?向量是离散的,所以累加,函数是接连的,那便是…….积分!
咱们知道函数内积是这样算的了,天然也就简略证明,依照这个方法去写的傅立叶打开,这些级数的确都是两两正交的。证明进程这儿就不打开了。好,下一个问题便是,为什么它们是正交basis如此重要呢?这就牵涉到系数的求解了。咱们研讨了函数f,研讨了级数,一堆三角函数和常数1,那系数呢?a0, a1, a2这些系数该怎样确认呢?好,比方我这儿预备求a1了。我现在知道什么?信号f(x)是已知的,傅立叶级数是已知的,咱们怎样求a1呢?很简略,把方程两头的一切部分都求和cosx的内积,即:
然后咱们发现,由于正交的性质,右边一切非a1项悉数消失了,由于他们和cosx的内积都是0!一切就简化为
这样,a1就求解出来了。到这儿,你就看出正交的美妙性了吧:)
好,现在咱们知道,傅立叶改换便是用一系列三角波来表明信号方程的打开,这个信号可所以接连的,可所以离散的。傅立叶所用的function basis是专门选择的,是正交的,是利于核算coefficients的。但千万别误解为打开改换所用的basis都是正交的,这彻底取决于详细的运用需求,比方泰勒打开的basis就仅仅简略的非正交多项式。
有了傅立叶改换的根底,接下来,咱们就看看什么是小波改换。首要来说说什么是小波。所谓波,便是在时刻域或许空间域的震动方程,比方正弦波,便是一种波。什么是波剖析?针对波的剖析拉(囧)。并不是说小波剖析才归于波剖析,傅立叶剖析也是波剖析,由于正弦波也是一种波嘛。那什么是小波呢?这个”小“,是针对傅立叶波而言的。傅立叶所用的波是什么?正弦波,这玩意以有着无量的能量,相同的起伏在整个无量大区间里边振动,像下面这样:
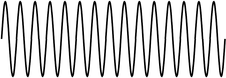
那小波是什么呢?是一种能量在时域十分会集的波。它的能量是有限的,并且会集在某一点邻近。比方下面这样:

这种小波有什么长处呢?它关于剖析瞬不时变信号十分有用。它有用的从信号中提取信息,经过弹性和平移等运算功能对函数或信号进行多标准细化剖析,处理了傅立叶改换不能处理的许多困难问题。恩,以上便是通常情况下你能在国内网站上搜到的小波改换文章告知你的。但为什么呢?这是我期望在这个系列文章中讲清楚的。不过在这篇文章里,我先点到为止,把小波改换的重要特性以及长处cover了,鄙人一篇文章中再详细推导这些特性。
小波改换的实质和傅立叶改换相似,也是用精心选择的basis来表明信号方程。每个小波改换都会有一个mother wavelet,咱们称之为母小波,一起还有一个scaling function,中文是标准函数,