纹波 电源
电子产品规划日益轻浮,使得电源模块亦须提高切换频率以缩小体积。藉由傅里叶级数频域剖析,研制人员将可把握切换式降压转换器电源模块输出端涟波改变量,然后调配最适合的电感和电容,使电路板尺度与动力功率到达最佳规划。
电子3C产品功用愈来愈丰厚且IC制程的进化趋向于低压大电流,使得芯片对电源的涟涉及噪声(Ripple Noise)要求更为谨慎。数字产品着重轻浮,相对地,电源模块为契合此要求必然提高切换频率以缩小外部零件体积。高频涟波与噪声对数字电路信号的影响必然严峻,尤其是影音(Video/Audio)信号及差动对数据传输信号(Differential Pair Signal)。
基于此要素,本文将以傅里叶函数(Fourier Series Expansion)办法来讨论同步交换式降压转换器(Synchronous Step Down Converter)输出电压纹波的波形,并依电容完好等效串联电阻(ESR)、等效串联电感(ESL)、电容值(Capacitance)对应的公式,经由理论推导,有用地剖析电源模块输出端纹波成分。
同步降压交换式转换器电路剖析
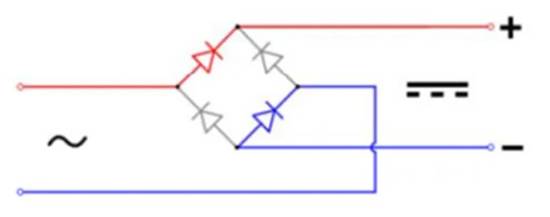
同步降压交换式电源转换器的运用电路如图1所示,体系作业原理是藉由交织式切换High Side (Q1)/Low Side (Q2)金属氧化物场效晶体管(MOSFET)(上、下桥晶体管),将输入能量转换成输出端恰当电压以供给到负载侧。体系关键性被迫组件电感及输出电容组成的低通滤波器(Low Pass Filter),用于传送与贮存能量并滤除沟通成分,让输出电压成为平顺的准直流需求。
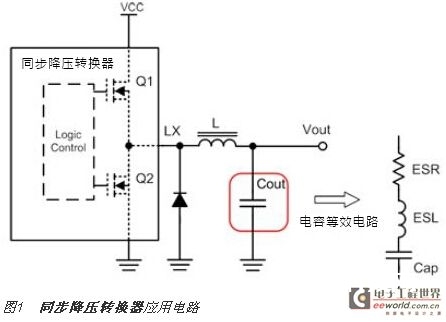
在惯例技能的认知下,当切换频率愈快,即可得到较小的输出纹波,若以流经电感电流乘上输出电容的等效串联电阻来预算峰值纹波电压是可得到近似数据,但与实践的输出纹波波形有程度上的差错,因此有必要考虑电容完好的等效电路特性,便可获得正确的回答。
在切换式降压转换器中,电感电流会对电容充电或放电,因此一切的纹波电流都会流经电容使得输出到负载的电压为安稳的直流电压Vo。但是,实践景象不是如 此,由于实践电容除了自身电容值外,还包含等效串联电阻与等效串联电感参数特性,让输出纹波电压(Ripple Voltage)ΔVo大于默认值,因此欲得到正确的输出纹波,则须将如图1所示完好的电容等效电路加以阐明。
其间,Cap全称为Capacitance,意思是电容值,其为电容最主要的参数,运用于电路稳压,补偿或滤噪声之用,可用电容公式来表明其特性,亦即Q = C·Vc或
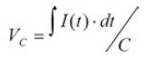
而ESR(Equivalent Series Resistance)为等效串联电阻,其为电容能量损耗及纹波的来历,可用欧姆规律来表明其特性,亦即
至于ESL(Equivalent Series Inductance),表明等效串联电感,可用电感微分公式来表明其特性,公式为
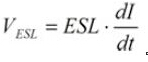
其感抗正比于频率,在低频时其感抗低,不易观测到其效果,但在频率较高时,其感抗添加,会下降电容稳压滤波的功用。别的要弥补的是,I为IL A.C成分,也便是电感电流的沟通成分。
一般来说,在稳态(Steady State)及负载固守时,输出电容的纹波电压主要是由电感的纹波电流形成,可先核算出电感的纹波电流,再使用欧姆规律,电感微分公式及电容电荷贮存公式,别离核算出ESR、ESL及Capacitance的纹波电压。再将此三种纹波加总起来,便可得输出电容的纹波电压,如公式1所示:
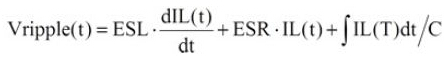
电感电流函数IL(t)可由公式2求得,其波形如图2所示。在Ton时(上桥MOSFET导通),输入电源VCC供给能量到负载端且电感组件贮存磁能(电感电流为线性递加),依据法拉第规律(Faradays Law):

将可得到导通周期(On-time Duty)电感电流斜率:
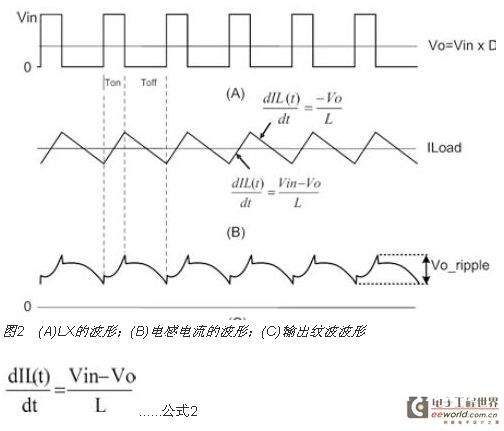
在Toff时(下桥MOSFET导通),电感开释能量到负载(电感电流为线性递减);其关断周期(Off-time Duty)电感电流斜率如公式3所示:
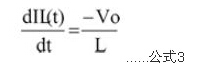
运用傅里叶函数频域剖析输出纹波波形
依傅里叶级数打开恣意周期性函数可得到频率信号的起伏,也代表着信号在不同频率重量成分的巨细。频域剖析是以输入信号的频率为变量,并能够供给比时域 (Time Domain)信号波形更直观且包含频率、振幅和相位信息。相对的傅里叶变换(Fourier Transform)可将频域函数转换成时域的稳态输出纹波Vo。因此,傅里叶级数与傅里叶变换的长处是可让剖析者依所供给的恣意输入波形,简单得到输出纹波波形。
周期T傅里叶级数为:
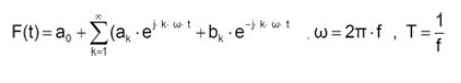
傅里叶系数则是:

ak及bk是共轭复数。等效电感阻抗包含ZESR、ZESL、ZCo,核算办法如下所示:
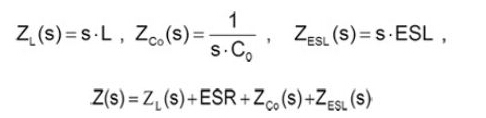
而LX电压波形运用傅里叶级数打开,表明如下:
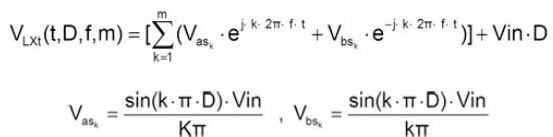
因此,ESR Ripple傅里叶级数打开如下所示:
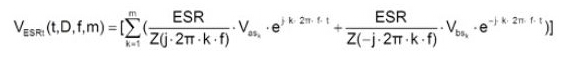
ESL Ripple傅里叶级数打开如下所示:
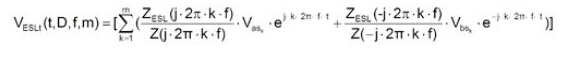
Cap Ripple傅里叶级数打开如下所示:

Vo Ripple傅里叶级数打开如下所示:
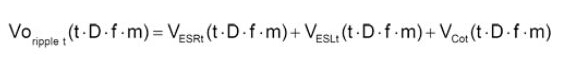
运用傅里叶变换数值剖析输出电压纹波
在处理信号时,常藉由傅里叶变换来获得信号所对应的频谱,然后再由频谱来读取信号的参数。但由于所做的核算量过于巨大,当处理很多的数据时,则需要快速计 算的算法,因此衍生出快速傅里叶变换(Fast Fourier Transform, FFT)。快速傅里叶变换大幅提高了频谱的核算速度。
快速傅里叶变换的运用条件包含:信号有必要是周期性的、取样周期有必要为信号周期的整数倍、采样率(Sampling Rate)有必要高于信号最高频率的两倍以上、取样点数N有必要为2k个数据。
快速傅里叶变换原理的表明法,则如下所示:

举例来说,当切换频率(fsw)为1050kHz的降压电路,输入电压为Vin=3.3伏特(V),Vo=1.8伏特,L=2.7微亨 (μH),Co=10微法(μF),ESR=4毫奥姆(mΩ),ESL=1.1奈亨(nH),fsw=280kHz。其实践量测的输出电压纹波、LX及电感纹波电流如图3所示。若给予恣意输入波形,由傅里叶级数剖析办法可得到对应的输出纹波,使用此办法供给一个快速有用的办法,可剖析核算输入恣意周期波的输出纹波。
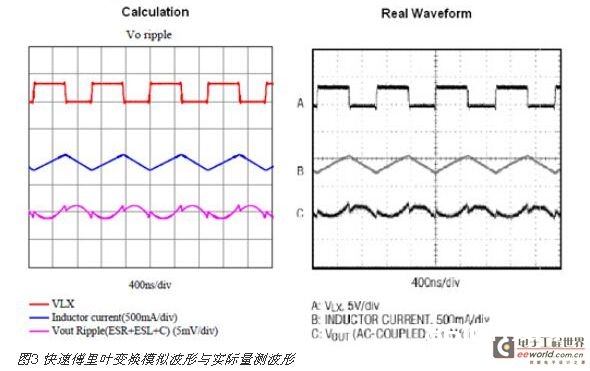
运用时域剖析输出纹波波形
时域剖析是以时刻函数(Time Function)表明信号之特性,依据时刻及振幅所组成之坐标平面来呈现出任何信号波形随时刻改变的瞬间物理量。时域剖析输出电压纹波阐明如下:

挑选恰当电感/电容值让规划优化
本文供给了傅里叶级数频域剖析,其特征便是无须求解杂乱的微分公式并与时域剖析相对应,充沛验证理论推导及实践量测波形的比照。意图是想以较谨慎的输出电容等效电路来剖析交换式降压转换器输出纹波电压。
经由上述证明可得知,电容的等效串联电阻、等效串联电感及电容值等特性均会影响输出纹波振幅及相位,并使用根本的奥姆规律、电感的微分公式推导电感与电流纹波改变,及电容器依据操作频率充/放电荷以保持输出电位安稳。
将上述三种影响纹波要素波形(等效串联电阻、等效串联电感及电容值)线性迭加,便可得到完好的输出纹波波形。透过此办法,可使研制工程师在规划切换式降压转换器电源时,依据电源需求及纹波答应改变量标准来挑选恰当的电感和%&&&&&%值,使其规划到达优化。