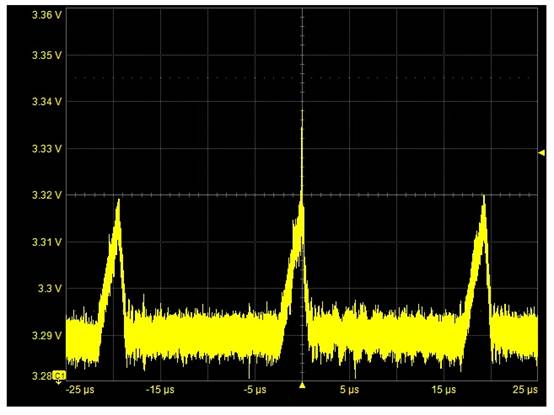
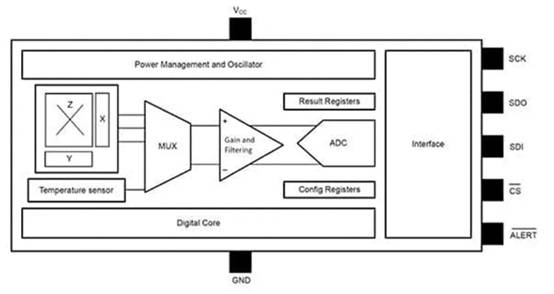
硬件规划：

整体思路：

整个机架选用PCB板，将四个电机固定在PCB板的四个角，外接电池。

硬件模块：

单片机、惯性丈量模块(IMU)、无线通讯模块、电机驱动模块、续流二极管、电源办理模块(稳压与充放电)、直流有刷电机、大电流放电电池、遥控器。

硬件选型：

硬件作业总述：

单片机担任整个体系的和谐作业；惯性丈量模块(IMU)担任丈量四旋翼的姿势；无线通讯模块担任四旋翼与遥控器的通讯；电机驱动模块担任驱动电机；续流二极管担任对电机进行续流；电源办理模块中的稳压模块担任整个体系的供电，电源办理模块中的充放电模块担任对电池充电；有刷电机担任供给四旋翼的飞翔动力；大电流放电电池担任四旋翼的能量来历；遥控器担任对四旋翼进行遥控和操控。

硬件规划功能模块图：

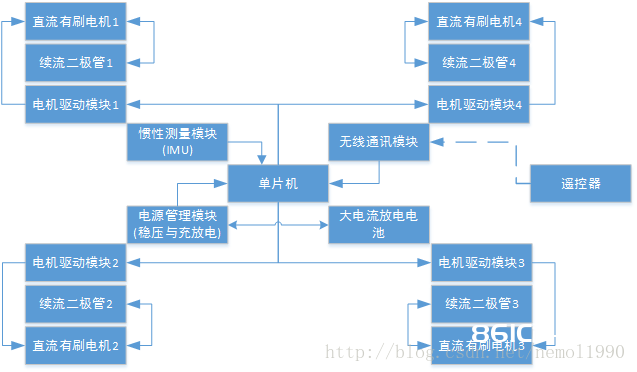
实践效果图与相关参数：

尺度：对角电机轴距10x10cm

重量：33.2g(带电池)

软件规划：

整体思路：

惯性丈量模块(IMU)丈量出当时飞机的三轴加速度与三轴角速度并传送给单片机处理，由单片机进行依据四元数的姿势解算，求解出当时飞机的pitch、roll、yaw三个视点值，然后依据这三个视点经过PID操控运算，输出四路PWM操控四个直流有刷电机的加减速然后到达飞机的平衡悬停。

其间，惯性丈量模块(IMU)的加速度计由于噪声比较大，所以需要对其进行滤波处理；而遥控器则是对飞机进行实时的姿势操控；最终由于四旋翼制造的特殊性，在调试PID参数阶段会频频的烧写程序，鉴于此，笔者开发了依据NRF24L01的Bootloader技能，免除了烧写Flash的物理连线约束，可完成长途程序一键下载。

姿势解算：

姿势解算归于四旋翼制造的中心部分，假如姿势解算可以实时的反应出飞机的状况，那么关于操控来讲就相对来说比较简单了。而姿势结算所要做的工作便是两个坐标系之间的正确转化(地舆坐标系与载体坐标系)，这种转化有许多种表明办法，例如欧拉角法、方向余弦矩阵法、四元数法、旋转矢量法等。笔者选用的是使用广泛的四元数法，而旋转矢量法则是一种依据四元数法的改善四元数法。

四元数本是用于描绘四维空间向量的一种办法，关于他的线性变换也便是在四维空间中的拉伸和旋转，清楚明了，咱们用四元数的向量乘法来表明三维空间中的旋转是捉襟见肘的。

经过惯性丈量模块(IMU)传送过来的当时飞机的三轴加速度和三轴角速度的值，这样一个三维的向量，转化为四维向量，然后在四维空间中做线性变换(也可以说在三维空间中旋转)后输出，使用四元数与欧拉角的联系(必定要留意旋转次序)，将当时四元数转化为欧拉角pitch、roll、yaw即得到当时飞机的姿势。

以下给出笔者姿势交融的代码，该代码网上都有，笔者在这儿做了少许注释，便利了解。

[cpp]view plaincopyprint?

2. voidIMUupdata(floatgx,floatgy,floatgz,floatax,floatay,floataz)
3. {
4. floatrecipNorm;//平方根的倒数
5. floathalfvx,halfvy,halfvz;//在当时载体坐标系中，重力重量在三个轴上的重量
6. floathalfex,halfey,halfez;//当时加速度计测得的重力加速度在三个轴上的重量与当时姿势在三个轴上的重力重量的差错,这儿选用差积的办法
7. floatqa,qb,qc;
9. gx=gx*PI/180;//转化为弧度制
10. gy=gy*PI/180;
11. gz=gz*PI/180;
13. //假如加速度计处于自由落体状况，可能会呈现这种状况，不进行姿势解算，由于会发生分母无穷大的状况
14. if(!((ax==0.0f)&&(ay==0.0f)&&(az==0.0f)))
15. {
16. //单位化加速度计,含义在于在改变了加速度计的量程之后不需要批改Kp参数,由于这儿归一化了
17. recipNorm=invSqrt(ax*ax+ay*ay+az*az);
18. ax*=recipNorm;
19. ay*=recipNorm;
20. az*=recipNorm;
22. //将当时姿势的重力在三个轴上的重量别离出来
23. //便是方向余弦旋转矩阵的第三列,留意是地舆坐标系(n系)到载体坐标系(b系)的,不要弄反了.假如书上是b系到n系,转置即可
24. //惯性丈量器材丈量的都是关于b系的值，为了便利，咱们一般将b系转化到n系进行导航参数求解。可是这儿并不需要这样做，由于这儿是对陀螺仪进行补偿
25. halfvx=g_q1*g_q3–g_q0*g_q2;
26. halfvy=g_q0*g_q1+g_q2*g_q3;
27. halfvz=g_q0*g_q0–0.5f+g_q3*g_q3;
29. //核算由当时姿势的重力在三个轴上的重量与加速度计测得的重力在三个轴上的重量的差,这儿选用三维空间的差积(向量积)办法求差
30. //核算公式由矩阵运算推导而来公式拜见http://en.wikipedia.org/wiki/Cross_product中的Mnemonic部分
31. halfex=(ay*halfvz–az*halfvy);
32. halfey=(az*halfvx–ax*halfvz);
33. halfez=(ax*halfvy–ay*halfvx);
35. //积分求差错,关于当时姿势别离出的重力重量与当时加速度计测得的重力重量的差值进行积分消除差错
36. if(g_twoKi>0.0f)
37. {
38. g_integralFBx+=g_twoKi*halfex*CNTLCYCLE;//Ki积分
39. g_integralFBy+=g_twoKi*halfey*CNTLCYCLE;
40. g_integralFBz+=g_twoKi*halfez*CNTLCYCLE;
41. gx+=g_integralFBx;//将积分差错反应到陀螺仪上，批改陀螺仪的值
42. gy+=g_integralFBy;
43. gz+=g_integralFBz;
44. }
45. else//不进行积分运算，只进行份额调理
46. {
47. g_integralFBx=0.0f;
48. g_integralFBy=0.0f;
49. g_integralFBz=0.0f;
50. }
52. //直接使用份额调理，批改陀螺仪的值
53. gx+=g_twoKp*halfex;
54. gy+=g_twoKp*halfey;
55. gz+=g_twoKp*halfez;
56. }
58. //以下为四元数微分方程.将陀螺仪和四元数结合起来，是姿势更新的中心算子
59. //核算办法由矩阵运算推导而来
60. //.1
61. //q=–*qxOmega式中左面是四元数的倒数,右边的x是四元数乘法,Omega是陀螺仪的值(即角速度)
62. //2
63. //.
64. //[q0][0-wx-wy-wz][q0]
65. //.
66. //[q1][wx0wz-wy][q1]
67. //.=*
68. //[q2][wy-wz0wx][q2]
69. //.
70. //[q3][wzwy-wx0][q3]
71. gx*=(0.5f*CNTLCYCLE);
72. gy*=(0.5f*CNTLCYCLE);
73. gz*=(0.5f*CNTLCYCLE);
74. qa=g_q0;
75. qb=g_q1;
76. qc=g_q2;
77. g_q0+=(-qb*gx–qc*gy–g_q3*gz);
78. g_q1+=(qa*gx+qc*gz–g_q3*gy);
79. g_q2+=(qa*gy–qb*gz+g_q3*gx);
80. g_q3+=(qa*gz+qb*gy–qc*gx);
82. //单位化四元数,含义在于单位化四元数在空间旋转时是不会拉伸的,仅有旋转视点.这相似与线性代数里边的正交变换
83. recipNorm=invSqrt(g_q0*g_q0+g_q1*g_q1+g_q2*g_q2+g_q3*g_q3);
84. g_q0*=recipNorm;
85. g_q1*=recipNorm;
86. g_q2*=recipNorm;
87. g_q3*=recipNorm;
89. //四元数到欧拉角转化，转化次序为Z-Y-X,拜见.pdf一文,P24
90. //留意此刻的转化次序是1-2-3，即X-Y-Z。可是由于画图便利，作者这儿做了一个转化，即互换Z和X，所以次序没变
91. g_Yaw=atan2(2*g_q1*g_q2+2*g_q0*g_q3,g_q1*g_q1+g_q0*g_q0–g_q3*g_q3–g_q2*g_q2)*180/PI;//Yaw
92. g_Roll=asin(-2*g_q1*g_q3+2*g_q0*g_q2)*180/PI;//Roll
93. g_Pitch=atan2(2*g_q2*g_q3+2*g_q0*g_q1,-2*g_q1*g_q1–2*g_q2*g_q2+1)*180/PI;//Pitch
94. }

留意其间的快速开方函数来自维基百科，精度0.175%。而且留意输入的陀螺仪有必要是弧度制(这一点在进入函数的时分现已做了转化)，不然姿势解算是过错的。

针对上述代码我还想阐明一个笔者发现的问题：有许多网友和许多外国的四轴代码(CrazyFlie)在这个姿势解算的加速度计部分都做了零点校准处理。意思便是在开机的时分读取必定次数的加速度计的值，然后均匀一下，得到一个初始状况的偏移量，最终在输出的时分加速度计减掉这个值，然后再给到姿势解算代码部分。而笔者在刚开始移植代码的时分是没有做这个零点校准处理的(当然，陀螺仪有必要要做零点处理，由于陀螺仪的原理，有必要要在停止时输出为0)，包含现在仍旧没有对加速度计做零点校准处理，依然可以获得较为实时的姿势。