根据单片机渠道的最小误差圆弧插补算法

在CNC机床的G代码中，最常见的有G0、G1、G2、G3代码，别离表明直线和圆弧插补，直线插补关于单片机来说，比较简略完成，只需求将位移增量转换为脉冲增量然后输出给步进电机就可以了，但关于圆弧插补，则需求单片机依据G指令中给出的起始点、半径、结束点这三个参数来操控X Y轴进行圆周运动；因而需求经过特定的圆弧插补算法来操控步进电机运动，圆弧插补算法比较多，常用的有逐点比较法、最小误差法和数字积分法等等，本文运用的是逐点比较法。

先不介绍逐点比较插补算法的原理，给出一幅图，下面再结合文字进行介绍。

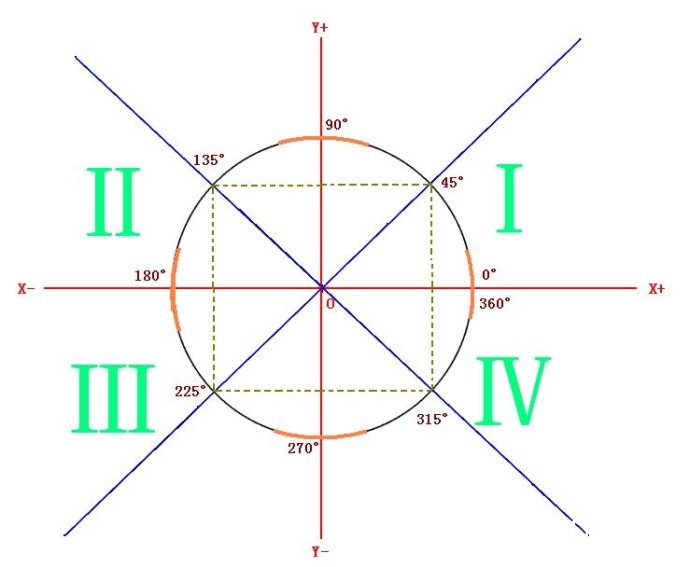
一、判别圆弧地点象限

在G代码的圆弧插补指令中，给出的圆弧可所以恣意象限的，而不同象限的圆弧制作算法又不相同，因而首要需求判别圆弧地点象限。当然给出的圆弧可所以在一个象限内，也可能是跨两个相邻的象限比方图中四段橙色的弧线。象限的判别比较简略，只需经过判别起始点坐标和结束点坐标的值便可。

二、找出圆弧运动过程中改动快的一轴

由上图可见，当圆弧坐落0～45度、135度～180度、180～225度和315～360度区域时Y的改动大于X且X坐标值的绝对值大于Y坐标的绝对值；而当圆弧坐落45～90度、90～135度、225～270度和270～315度区域时X的改动大于Y且X坐标值的绝对值小于Y坐标的绝对值，因而可经过XY坐标值的比较来找出运动过程中改动快的一轴。

三、误差核算与判别

假如咱们给改动快的那一轴（假定是X）进给一个脉冲，则加工点到圆心的间隔会发生改动，而Y轴是否进给，则经过误差核算来判别。

众所周知：圆心在坐标原点的圆方程为

x*x+y*y=r*r；

设误差F＝x*x+y*y－r*r；

假定Y轴不进给，则F1＝（x＋1）*（x＋1）+y*y－r*r；

假定Y轴进给，则F2＝（x＋1）*（x＋1）+（y＋1）*（y＋1）－r*r；

比较F1和F2的绝对值，假如不进给时的误差小，则Y轴进给，不然Y轴不进给。

若没到结尾，则一向循环。

留意：电机动动的方向需求经过判别象限来决议的。

四、结尾判别

假如抵达结尾则表明弧线制作结束，退出插补循环体。

五、跨象限的圆弧段处理

跨象限的圆弧段处理也依照上述办法，挑选一改动快的轴进给，另一轴经过误差来判别是否进给。电机运动的方向相同经过象限来判别。

自己之前测验过给改动快的轴进给N个脉冲量，再经过解圆的方程来核算出Y的脉冲进给量，因为解圆的方程需求进行开根号运算，因而影响了插补的速度，一起一次进给N个脉冲量会使电机运动不接连，更重要的是加工的精度会有很大的影响。选用以上办法，不光减少了很多的运算时刻，进步了插补的速度，精度也得到了很大的进步。

该办法简略，便于了解，也适合在单片机渠道上运转。

以下是某一象限的顺时针圆弧插补代码，其它象限相似：

#definee(x,y)(x)*(x)+(y)*(y)-r_r//误差核算r_r为半径的平方

#define DT 1

//假如在榜首象限

case 1:

while(y>x)// 45°-90°，此段X值改动比Y快

{

k=orig_x+x;//orig_x原点坐标

MoveToPosition(k,orig_y+y);//移动电机至方针方位

x+=DT; //优先改动X

f=e(x,y); //Y不变时所得点距圆周误差，

g=e(x,y-DT); //Y变时所得点距圆周误差，

if(abs_16(f)>=abs_16(g)) y-=DT; //假如变时误差小，则取改动Y

if(k>=end_x)goto Exit;//假如抵达结尾，则跳出循环体

}

while(x>=y)//0-45°，此段Y值改动比X快

{

k=orig_y+y;

MoveToPosition( orig_x+x,k);//移动电机至方针方位

y-=DT; //优先改动Y

f=e(x,y); //X不变所得点距圆周误差，

g=e(x+DT,y);//X改动，所得点距圆周误差，

if(abs_16(f)>=abs_16(g))x+=DT;//假如变时误差小，则取改动X

if(k<=end_y)goto Exit;//假如抵达结尾，则跳出循环体

}

break;