差错补偿技能在加工精度要求较高的数控机床中得到了广泛的运用,但在轿车零部件(如后桥衬套、轮毂轴承等)的压装体系中非常罕见。跟着轿车行业和工业自动化的开展,轿车零部件压装的技能标准也日渐严厉。从开端对零部件的机械工艺、压入平整度等以人眼经历判别为主的要求,到后来对压入结尾力、压装要害点力等以特别点压力值合格为主的要求,再到如今,除了重视压装要害点目标,还开端重视压装进程某区间的目标改动量。如某款轿车的后桥衬套压装中,要求压力从3 kN上升到19 kN时,衬套相对后桥的位移量在2.10 mm到4.25 mm之间。
现在轿车零部件压装设备多为半闭环伺服操控办法,经过将其改造为全闭环办法能够有用消除半闭环办法的体系差错,进步操控精度,但这种做法不只会消耗较大的时刻本钱和资金本钱,并且很简略遭到出产环境影响而引进新的更大的差错。因而,本文在不改动原有半闭环办法的基础上,提出了一种依据体系标定和插值的差错补偿办法。
1 半闭环伺服压装体系差错剖析
1.1 体系模型
图1为常见的半闭环伺服压装体系:上位机经过向伺服操控器给定操控速度和方位,操控运动组织进行轴向的压装动作,一起上位机经过监控运动组织的位移和压力进行实时操控调整。
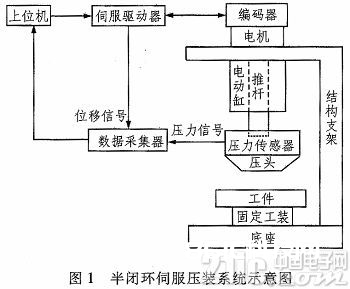
1.2 差错来历
在半闭环伺服压装体系中,压力传感器一般安装在压头上,经过调整使压力传感器、压头、工件的中轴线重合,并依据作用力与反作用力持平的理论,可保证压力传感器反应的压力能够代表工件的轴向受力。与此一起,压装反应的位移来自编码器,它反映的是电机输出转速和累积位移。从编码器到工 件之间,别离串连了电机、电动缸和压头号组织,它们全体固定在由底座和结构支架构成的压装渠道中。上述组织平和台自身以及相互之间或许存在以下的静态差错和动态差错:
1)组织间的传动空隙差错;
2)电动缸中螺杆导程转化差错;
3)机械热形变差错;
4)底座和结构支架受力后的形变差错;
5)运动进程中的设备轰动导致的差错等。
以上差错在不同程度上添加了体系的位移差错,使得编码器反应的位移并非工件实践位移。关于各类差错,其他学者或业界人士都提出了有用的检测和补偿计划,可是因为体系差错来历的多样性和设备的复杂性,别离检测和补偿各项差错是好不容易的。因为全闭环办法比较半闭环办法的差异在于,前者不需要逐个剖析中心组织的各项差错,而是经过将反应组织移动到运动组织结尾,直接躲避了中心组织的上述差错。因而,结合全闭环办法的差错躲避特性,在半闭环操控办法基础上,运用上位机对数据的快速算法化处理优势,提出了一种经过预先标定、树立差错表格和表格插值的差错补偿办法。
2 标定和补偿
2.1 差错标定
规划如图2所示的标定设备。
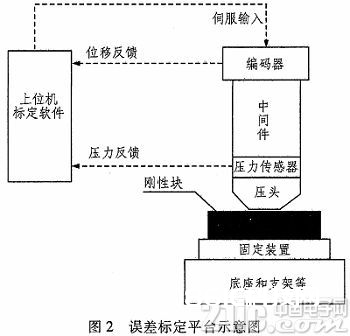
图2中的中心件为电机、电动缸及其推杆等。标定渠道树立进程非常简略便利,仅需要将原设备中的工件和用于固定工件的工装撤消,替换以均匀刚性块和用于固定刚性块的设备,并留意调整刚性块中轴线与压头进给轴线重合。
刚性块的特性在于它在必定压力极限内(应大于最大压装力)不发生形变,假定该伺服体系不存在差错,那么当操控压头对刚性块由小到大施加压力时,位移值将坚持不变;反之,假如压力添加进程中位移发生改动,那么阐明存在体系差错,且恣意两个压力值所对应位移的差值即为此压力间的体系位移差错。由此咱们能够得到一系列成对的压力和位移值,并以此树立体系差错表格。稍后即可运用差错表格进行位移差补偿。
2.2 补偿算法
因为标定采样的压力一位移数据为离散方式,故在运用该表格时应进行插值查找。关于插值办法,常用的有Lagrange插值法、Hermite插值法、Newton插值法、最小二乘插值法等。在工程实践中,因为出产条件的复杂性,不可控因素的多样性,采样数据在部分的规律性较差,选用一般的插值办法在低次插值时准确度大大下降,而在高次插值时又会很大程度上添加算法的时刻复杂度。因而,归纳考量工程实践对算法速度和精度的要求以及标定表格的数据特征,挑选依据部分最小二乘的线性插值法。
依据最小二乘法线性拟合的基本原理,给定一组试验数据(xi,yi)(i=1,2,…,m)求出自变量x和因变量y的线性关系式:

将求得的a0和a1代入式(1)中,得到试验数据的最小二乘法线性拟合关系式。
因为在本例中进行的是部分插值,因而需要从标定好的差错表格中选取部分的数据规模(拟合点数)。这儿咱们以待插值点作为中心点,前后取N个点作为拟合点进行最小二乘
线性拟合。

至此便得到插值点(X,Y)。同理可求得另一个压力值Y’(Y
δx=X’-X (7)
3 试验成果
本文的数据样本来自某品牌轿车的后桥衬套压装机的实践出产数据,该后桥衬套的压装工艺要求:在衬套压入进程中压力从3 kN上升到19 kN时,位移量在2.10~4.25 mm之间为合格。咱们运用20 cm×20 cm×10 cm的刚性块作为标定辅佐设备,以100 Hz的采样率对压力和位移进行采样,构成差错标定表格,并以N=10为拟合点数进行最小二乘法线性插值。别离取标定表格中3 kN和19 K前后10个点的数据,见表1和表2。
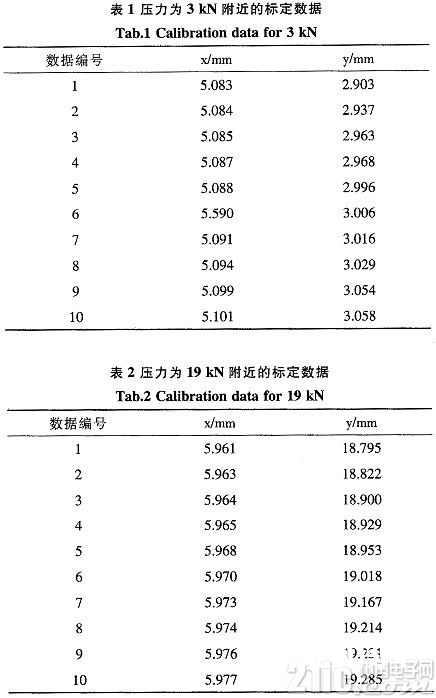
依据上文的插值规矩,核算如下:
1)对表1进行最小二乘法拟合所得关系式为y=37.1606+7.888 72x,将y=3带入上式,得压力为3 KN时的插值位移为5.090 89 mm;
2)对表2进行最小二乘法拟合所得关系式为y=-149.003+28.1507x,将y=19带入上式,得压力为19 KN时的插值位移为5.967 98 mm;
3)令X=5.090 89,X’=5.967 98带入式(10),得到体系位移差错为0.877 mm。
随机选取10组车间出产数据,提取出补偿前压力从3KN上升到19 KN时的位移量数据,并判别是否在工艺上要求的压装合格区间[2.10 mm,4.25 mm],见表3:
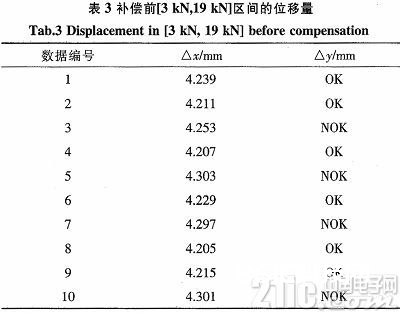
补偿前这10组产品数据合格率为60%,将表3数据别离减去现已求得的体系位移差错0.877 mm,即得到补偿后的位移值,判别补偿后的位移值是否在合格区间[2.10 mm,4.25mm],见表4。
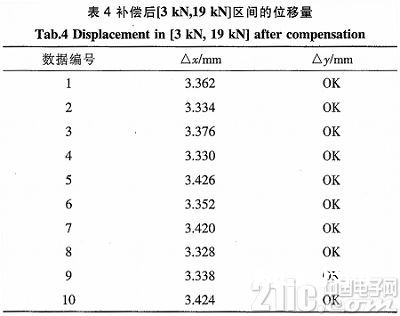
由表4知,补偿后的数据在工艺要求上的合格率为100%。
为进一步确认差错补偿的准确性,咱们运用数显千分表,将表座固定在压装体系底座上,将表头安装在压头端,使测杆与压头进给轴线平行,对压力在[3KN,19KN]区间的位移进行实测,得到五组数据如表5。
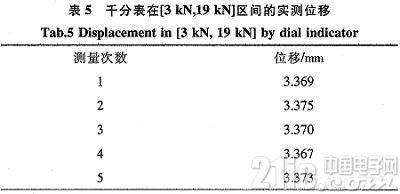
求得表5中位移平均值为3.371 mm,将表3和表4中的位移量别离与该平均值比较:
1)补偿前位移量对干分表实测位移的平均偏差为26.0%
2)补偿后位移量对千分表实测位移的平均偏差为1.02%。
由此可见,经过补偿能够使位移到达杰出的准确度,极大地进步产品合格断定的可靠性。
4 结束语
本文针对轿车零部件压装体系,在原有的半闭环伺服操控体系基础上,规划了一种依据刚性块辅佐的差错标定和依据最小二乘法拟合的插值补偿办法。经过工程实践的验证,该办法简洁且操作性强,对补偿半闭环压装体系的差错缺点有明显的作用。