摘要:针对铅垂平面内的外弹道模型,对依据LabVIEW的弹道解算办法进行研讨,提出了以四阶龙格库塔算法为中心的解算办法。运用LabVIEW编写了弹道解算程序,在初始点状况已知的情况下,快速高效的递推出外弹道轨道与落点坐标。程序可以对数据进行处理与显现。人机界面友爱,易于操作。关于外弹道解算具有必定的运用价值。
现代导弹从呈现现已过去了50多年,这50年傍边导弹技能不断发展。其间包含了伴随着导弹而发展起来的新式学科-外弹道学,它不只研讨导弹飞翔进程中质心的运动进程还研讨了姿势操控学与制导理论等。外弹道学触及到的技能规模广且需求各个学科彼此联络。本文研讨的是铅垂平面内,弹丸质心的运动轨道,树立质心运动方程组,已知弹丸初始状况运用四阶龙格库塔办法求解发射轨道。据此编写了LABVIEW程序完成解算进程而且将轨道显现出来。
1 质心运动方程
研讨弹丸质心的运动进程,第一步要做根本假定;
1)整个发射至击中方针的运动进程中,攻角为0。
2)弹丸是轴对称的。
3)地上为平面。
4)飞翔进程中重力加速度巨细不变且笔直向下。
5)科氏加速度为0。
6)大气条件为标准大气条件,无风。
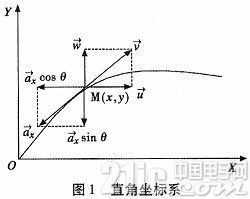
在此根底之上,作用于弹丸的力只要重力与空气阻力。依此弹丸的质心运动方程为式(1)。
因为ax=cHτ(y)G(vτ)v,所以得到了弹丸质心的运动方程组为式(2)。
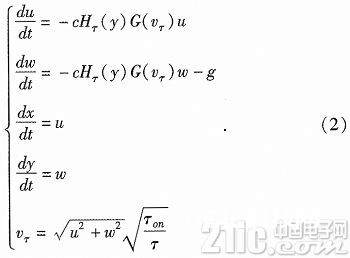
式中:ax为空气阻力加速度;c为具有弹丸特征的弹道系数;H(y)为空气密度函数;G(v)为阻力函数。
2 四阶龙格库塔
四阶龙格库塔法广泛用于模仿仿真运用中的弹道解算,在工程中被称为“高精度单步算法”。由欧拉公式导出,k1为一阶精度的欧拉公式,k2用xi点处的k1与xi+1的k2的
均匀值作为均匀斜率的近似值。就会得到二阶的欧拉公式。以此类推得到四阶龙格库塔方程如式(3)所示。龙格库塔法因单步四次核算,核算量大,因而广泛运用于核算机仿真核算。
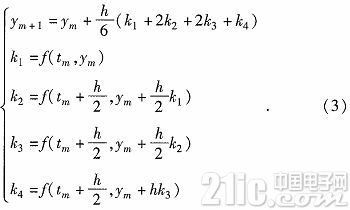
3 程序设计
依据弹丸质心运动方程组,运用四阶龙格库塔法,在LABVIEW软件渠道编写软件解算弹道轨道。在LABVIEW中依据Runge-Kutta算法VI树立解算方程。Runge-KuttaVI如图2所示。
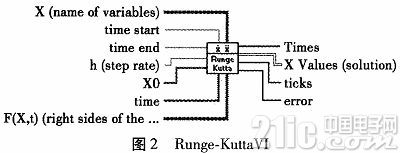
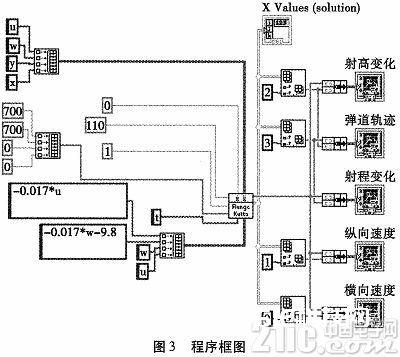
此VI需求初始状况的数据。依据弹丸质心运动方程组,初始点已知。当t=0时,x=0;y=0;u=V0COSθ0;w=vosinθ0。θ0为发射角已知。X(name of variables)为变量称号将质心运动方程组所触及的变量名设置为字符串数组。time start为初始时刻为0,time end为完毕时刻。h(steprate)为步长设置为1。X0为对应于X变量名的数据信息,这儿设置u=700;w=700;y=0;x=0。time设为t。F(X,t)为对应变量名的函数名。程序设置如图3所示。
4 定论
以固定的弹体,在标准大气压条件下,c为常数;x,y为0;纵向与横向初速度别离设为100、200、300、400、500。记载解算数据:时刻、最大高度、最远间隔如表1所示。
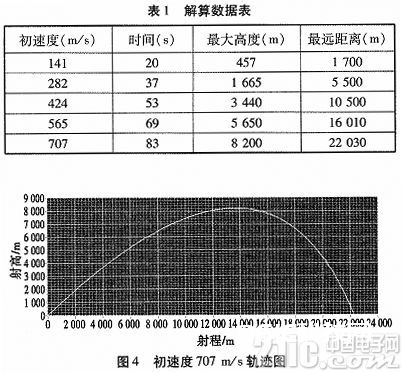
初速度为707 m/s解算出的轨道曲线如图4所示。
通过数据仿真试验,得出定论。此弹道解算软件具有可靠性,解算出的弹道数据对弹道研讨具有必定的现实意义。