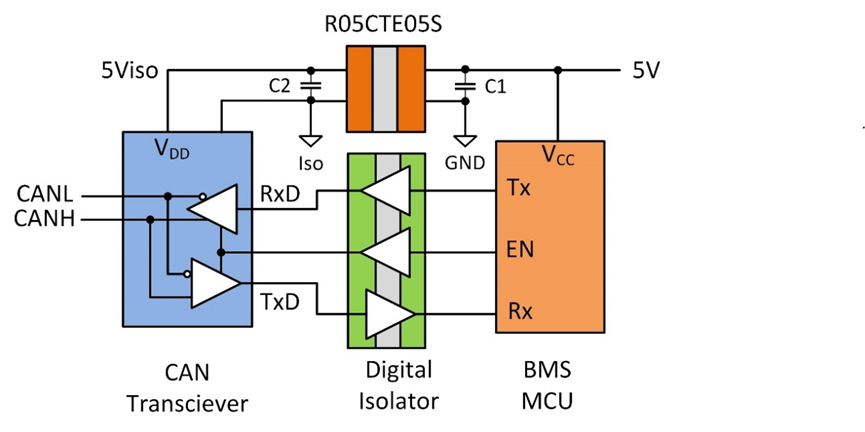
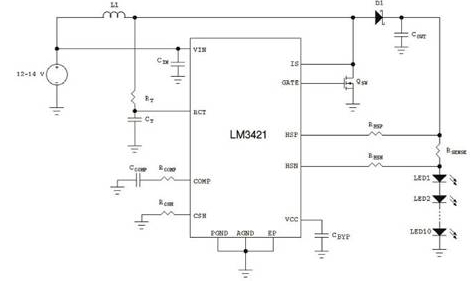
程学农(中电海康集团无锡研究院，江苏 无锡 214061)
摘 要：介绍了经过史密斯圆图进行阻抗匹配使信号有用的传输到负载，本文着重于RFOUT与天线之间的匹配。NB-IoT模块供给1个RF天线PAD供天线运用，经过运用电容和电感等元器件组成π形匹配电路，用于调理天线端口的功能，线路阻抗保持在50 Ω左右。经过对负载阻抗进行归一化，画出其圆。负载阻抗的实数部分与阻抗圆和导纳圆有2个交点，其对应的x值为
的x值与负载阻抗的x值之差，所以两者的差为匹配网络需求串入归一化电抗值，经过复原，可得串联元件值，同理，经过导纳圆可求得所需并联元件值。
要害词：反射系数；负载阻抗；特征阻抗；史密斯圆图驻波比
0 导言
NB-IoT (窄带蜂窝物联网)聚集于低功耗广掩盖（LPWA）的物联网商场，是一种可在全球范围内广泛运用的新式技能。具有掩盖广、衔接多、速率低、成本低、功耗低、架构优等特色，未来将会大规模地遍及。因而跟着NB-IoT模块的运用和开展，怎么快速有用地对其运用规划成为了要害。现阶段，市面上大都NB-IoT模块的运用都较简略，选用UART进行数据传输，所以运用规划的要害点在于天线部分。一般，合格的RF电路一般反射系数小于1/3，为了使电路的发射系数在一个合格的范围内，需经过阻抗匹配的方法来完成。
一般完成阻抗匹配的方法能够分为四大类：①核算机仿真；②手艺核算；③经历；④史密斯圆图。核算机仿真运用的条件是需求对其原理较通晓；如不通晓，简单在参数设置上发生过错。手艺核算的缺陷是较繁琐，需求很多的核算量，消耗时刻。经过经历的方法也有着较大的局限性，不适合一切人。面临以上方法所呈现出的缺陷，史密斯圆图能够在不作任何核算的条件下得到一个准确的阻抗匹配，避免繁琐的核算进程。凭借史密斯圆图能够用图解法解出天线阻抗的匹配网络，其精准度与史密斯圆图的精度相关。
1 阻抗匹配
天线和馈线的衔接处称为天线的输入端，天线输入端的电压与电流的比值称为天线的输入阻抗，表达式为R jX + ，其间实数部分为输入阻抗( R )，虚数部分为输入电抗(Xi)。天线的匹配便是消除天线输入阻抗中的电抗重量，使电阻重量尽可能地挨近馈线的特性阻抗。阻抗匹配的意图是使功率最大化，避免能量从负载反射回信号源，以及避免频率牵引现象的发生 [1] 。阻抗匹配的方法是在负载和源之间结构一个匹配网络，是其阻抗等于负载的复阻抗的共轭，如图1所示。
2 反射系数
信号不能差异什么，能感遭到的只要阻抗。假如信号感遭到的阻抗是稳定的，此刻信号正向传达。假如阻抗发生了改变，信号就会发生反射。衡量反射量的目标为反射系数，反射系数为单端口散射参数（S-parameter）里的S11 [2] ，是归一负载值，是发射电压与传输电压之间的比值，其表达式为：
(Z O为特征阻抗，为实数）
假定1：PCB线的特征阻抗为50 Ω，假如遇到一个200 Ω的贴片电阻，不考虑寄生电容电感的影响，那么反射系数为
，意味着信号有3/5被反射回源端。在RF电路中，反射系数越挨近0越好，绝对值要小于1/3。
假定2：终端接负载阻抗 Z L = 125+50j ，那么反射系数为:
驻波比VSWR=3.04
当VSWR=1时，标明彻底匹配，实践运用中，VSWR要小于1.2。所以上述情况为失配。一般，匹配的程度能够经过反射系数、行波系数、驻波比和回波损耗这几个参数来进行衡量。
3 运用史密斯 圆图进行阻抗匹配
3.1 史密斯圆图介绍
已知反射系数Γ的表达式:
由于 Z O 是一个实数，因而能够将其固化
经过式(1)和式(2)，能够得到：
经过式(3)能够得到：
经过收拾，终究得到式(13),能够了解为在复平面
图3a标明圆周上的点具有相同实部的阻抗，如r =1的圆，标明(0.5, 0)为圆心，半径为0.5。它包含了代表反射零点的原点(0, 0)。以(0, 0)为圆心、半径为1的圆代表负载短路。负载开路时，圆退化为一个点(以1, 0为圆心，半径为0)。
同理，经过式(5)和式(6)可推导出：
式(18)标明晰在复平面( Γ r,Γi )上的圆的参数方程 (x-a)2+(y-b)2=R2，它的圆心为( 1,1/ x )，半径1/ x。
同理，图3b标明晰圆周上的点有相同虚部 x 的阻抗。一切的圆(x为常数)都包含点(1, 0)。与实部圆周不同，x的值可为正或负，复平面下半部是其上半部的镜像。将两簇圆周放在一同。能够发现一簇圆周的一切圆会与另一簇圆周的一切圆相交。因而，假定已知阻抗为r+jx，只需求找到对应r和x的两个圆周的交点就能够得到其反射系数。
举例如下。
(1) 已知特性阻抗为50 Ω，负载阻抗如下：
(2) 对负载阻抗进行归一化
(3) 经过原图中的直角坐标或许极坐标能够读出其发射系数（图4a和图4b）
(4)在史密斯圆图上显现其坐标(如图5)
(5)在圆上读出反射系数、驻波等到回波损耗
画图法：衔接圆心到负载点 Z2 ，以这条直线为半径，实轴中点为圆心画圆，在圆与实轴左面的交点上画图一条直线，读出值（如图6）。
3.2 怎么串并电感电容
图7中心的水平线为纯阻抗线，水平线上的点标明纯电阻。实轴上半平面(x < 0)是理性阻抗的轨道，实轴上下平面(x > 0)是容性阻抗的轨道，在上方的点用电路标明可认为是1个电阻串联1个电感，在下方的点则为1个电阻串联1个电容 [3] 。圆则代表等阻抗线，指落在上面的点的阻抗都持平。因而，能够在图8标明出来。
串联电感：阻抗原图中等电阻圆上顺时针旋转；
并联电容：阻抗原图中等电阻圆上逆时针旋转；
并联电感：导纳圆图中等电导圆上逆时针旋转；
并联电容：导纳圆图中等电导圆上顺时针旋转；
3.3 N B-IoT 模块实践事例：
3.3.1 N B-IoT 天线匹配网络
以图9为例，模块供给1个RF天线PAD供天线运用。C1、C2、R2三个%&&&&&%组成 π 形匹配电路，用于调理天线端口的功能。一般情况下，在PCB布线时，为了避免信号反射线路阻抗尽量保持在50 Ω左右。为了削减核算量以及杂乱程度，首要能够考虑先运用电容和电感进行匹配。进程如下。
NB-IoT模块的发射频率为900 MHz，天线阻抗Z=60+50j ，馈线阻抗W=50 Ω。
(1) 归一化：
(3)挑选一个交点J1：0.91∆b=0.5 – (-0.41)=0.91
(4)求交点的对称点（阻抗）的值
(5)求串联元件值
(6)对应网络图（图11）
(7)同理，能够核算第2个交点，方法相同。3.4 π形网络（图12）
当交点J2与Y点的差值较小时，Y点跳过J2点持续向下移动至P点，此刻咱们能够经过上述的方法进行π形网络的匹配。
(7)对应π形网络如图13
4 总结
上述比如叙述了NB-IoT天线匹配网络的操作进程，经过史密斯圆图，能够直接读出电路的反射系数、驻波比等参数，削减繁琐的核算，进步功率。当反射系数觉得值小于1/3可认为此电路合格。当反射系数大于1/3，经过对其进行串并%&&&&&%，电感进行阻抗匹配，直至反射系数小于1/3停止。如需更精准的匹配，则可经过核算机仿真等其他方法来进行阻抗匹配。
参考文献：
[1] 陈俊夫.关于Smith圆图的运用和了解[J].我国新通讯, 2015(17):48-48.
[2] 杜广超.史密斯圆图在天馈体系中的运用[J].科技风,2012(4):73-73.
[3] CHAN K C.使用史密斯圆图规划匹配网络[J].无线电工程,2001, 31(12):51-53.
[4] 王延平.使用smith圆图快速求解阻抗匹配网络[J].有线电视技能,2013,(12):95-98.
[5] TORUNGRUENG D,THIMAPORN C.A generalized ZYSmith chart for solving nonreciprocal uniform transmission‐line problems[J]. Microwave and Optical TechnologyLetters,2004,40(1): 57-61.
（注：本文来源于科技期刊《电子产品世界》2020年第06期第76页，欢迎您写论文时引证，并注明出处。）
