uC/OS之安排妥当表常识

安排妥当是什么呢?它便是全部预备安排妥当了，预备运转了。使命一旦树立，它就会进入了安排妥当态(task ready)，预备运转了。使命的树立可所以在多使命运转开端之前，也能够动态地由一个运转着的使命树立。

那么，假如有多个使命安排妥当，那怎样办呢?这就牵涉到了安排妥当表的问题了。安排妥当表(ready list)在寄存安排妥当使命的。安排妥当表中有两个变量，OSRdyGrp和OSRdyTbl[]。由于使命最多一般只能是64个，Jean J.Labrosse 就把安排妥当表分红8*8的一个矩阵形表(table)，这样就刚好能寄存64个安排妥当的使命了。下面表格里边的数字代表优先级。那么，OSRdyGrp和OSRdyTbl[]又代表什么呢?

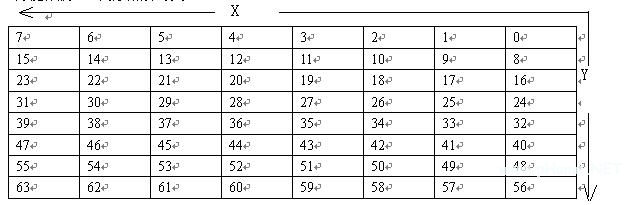
见上图，作者见使命太多，就按优先级将它分红了八组，每一行作为一组，每组八个使命，(也即按Y坐标分组)。而OSRdyGrp是一个有八位二进制数的数，它的每一位代表一个组。比方：OSRdyGrp的第0位代表了榜首行0到7这八个优先级。榜首位代表了8到15这八个优先级，以此类推。只需哪一组中的任何一方位位(即哪一组中有任何一个使命进入安排妥当表)，那么OSRdyGrp相应的位就置1。比方：榜首行中优先级0到7，只需有一个使命进入安排妥当表，那么OSRdyGrp的第0位就会置1(有更多使命进入安排妥当表也会置1)，表明这一行中有使命进入安排妥当表啦，但是有多少呢?不知道!

那不知道，怎样办呢?这就要看OSRdyTbl[]了。先来介绍一个掩码的常识：ucos里边有一个数组，叫OSMapTbl[]，它来协助咱们查一个使命是否进入优先级。

详细如下：

咱们来看，一个使命优先级将它化成二进制数，它的低三位与它在哪一组没有使命联系!由于逢八才换组，而低三位最大才是七!但它能决议这个使命在一组的某个当地(即能决议X的值)而它的接下去三位与它在一组中的哪个方位没有任何联系!由于去掉低三位，接下去三位一直是八的倍数，一直指向组的首地址!但它能决议Y的值!这样，在一个矩阵中，X的值和Y的值都决议了，那么这个使命地点的方位就决议了。这样，使一个使命进入安排妥当状况和脱离安排妥当状况也就简略了。

其实咱们不必这么费事,咱们看,咱们能够把表中的数看成是八进制的数,低三位看成是个位,接下来三位看成是进位,进位代表OSRdyGrp,个位代表OSRdyTbl[],个位不管怎样变,它都不会影响进位的方位，所以在哪一行只取决于OSRdyGrp，在哪一列只取决于OSRdyTbl[]，口算也算出来了，呵呵。这样比较好了解一些。

这儿或许咱们有疑问：那不只取了优先级的六位吗?还有两位呢?这个不必着急，还有两位为零!由于最大才63，只需要用到六位，假如最高两位有任何一位为一的话，就会犯错。所以咱们就不必管最高两位了。

使使命进入安排妥当状况的程序为：

OSRdyGrp |= OSMapTbl[prio>>3];//确认它的行，置1

OSRdyTbl[prio>>3] |=OSMapTbl[prio0x07];//确认它的列，置1

找出进入安排妥当态的俦优先级最高的使命

理解了上面的内容，这儿也不难理解了。这儿作者Jean J.Labrosse 供给了一个查找表的，只需依照必定算法查找，很快就查出来了。

代码为：y = OSUnMapTbl[OSRdyGrp];

x= OSUnMapTbl[OSRdyTbl[y]];

prio = y3 +x;

这个表为：

右边注释的值是代表OSRdyGrp的值。假如OSRdyGrp的值为01101000，即0x68，那么，咱们能够依据右边的注释，要查第七行。是第七行的第八个(从0开端)。是3。再代入程序，算出x为2，将x和y 代入prio = y3 +x;，算出最高为26，再依据这个值，查出使命操控块优先级表，得到该使命的使命操控块。