作者:胡侨娟;仲顺安;陈越洋;党华
跟着核算机和信息技术的快速开展,人们对微处理器的功能要求越来越高。乘法器完结一次乘法操作的周期基本上决议了微处理器的主频,因而高功能的乘法器是现代微处理器中的重要部件。本文介绍了32位浮点阵列乘法器的规划,选用了改善的Booth编码,和Wallace树结构,在削减部分积的一起,使体系具有高速度,低功耗的特色,而且结构规矩,易于VLSI的完结。
1乘法核算公式
32位乘法器的逻辑规划可分为:Booth编码与部分积的发生,保存进位加法器的逻辑,乘法阵列的结构。
1.1Booth编码与部分积的逻辑规划
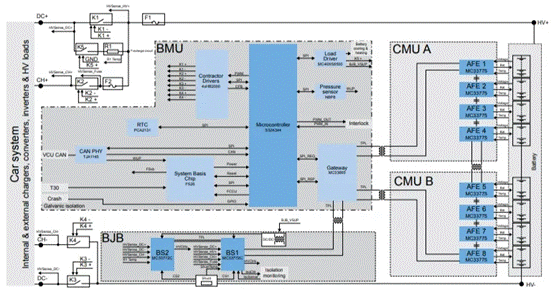
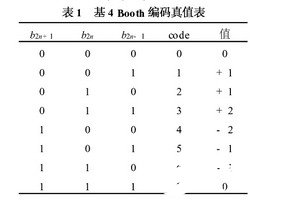
尾数的乘法部分,本文选用的是基4Booth编码办法,如表1。首要规则Am和Bm表明数据A和B的实践尾数,P表明尾数的乘积,PPn表明尾数的部分积。浮点32位数,尾数是带隐含位1的规范化数,即:Am=1×a22a21….a0和Bm=1×b22b21.…b0,因为尾数全由原码表明,相当于无符号数相乘,24×24位尾数乘积P的公式为:
![]()


1.2乘法器的阵列结构
本文选用的是3-2加法器,输入3个1位数据:a,b,ci;输出2个1位数据:s,Co。运算式如下:
![]()
其逻辑表达式如下:
![]()
![]()
当每个部分积PPn发生之后,将他们相加便得到每个乘法操作的成果。相加的过程有许多,可选用的结构和加法器的品种也许多。比方串行累加:
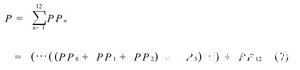
而Wallace树的乘法阵列如下:
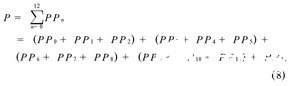
加法器之间的衔接联系如图1,图2所示,或许从公式(7)与(8)中可以看出,图1中串行累加的办法推迟为11个3-2加法器的推迟,而图2中,Wallace树推迟为5个3-2加法器的推迟。图1的推迟比图2的推迟大。


图1串行累加图2Wallace树
232位浮点乘法器的规划
本文是针对IEEE754单精度浮点数据格局进行的浮点乘法器规划。IEEE754单精度浮点格为32位,如图3所示。设A,B均为单精度IEEE754格局,他们的符号位,有用数的偏移码和尾数部分分别用S,E和M来表明。双精度和单精度选用的运算规矩是共同的,仅仅双精度的位长增加了一倍,双精度是64位,其间尾数52位,指数11位,1位符号位。所以提高了精度规模。
![]()
图332位浮点数据格局
32位浮点数据格局:A=(-1)S×M×2E-127。其间乘法器运算操作分4步进行。
(1)确认成果的符号,对A和B的符号位做异或操作。
(2)核算阶码,两数相乘,成果的阶码是两数的阶码相加,因为A和B都是偏移码,因而需求从中减去偏移码值127,得到A和B的实践阶码,然后相加,得到的是成果的阶码,再把他加上127,变成偏移码。
(3)尾数相乘,A和B的实践尾数分别为24位数,即1×Ma和1×Mb,最高位1是躲藏位,浮点数据格局只显示后23位,所以尾数相乘成果应为一个48位的数据。
(4)尾数规范化,需求把尾数相乘的48位成果数据变成24位的数据,分3步进行:
①假如乘积的整数位为01,则尾数已经是规范化了;假如乘积的整数位为10,11,则需求把尾数右移1位,一起把成果阶码加1。
②对尾数进行舍入操作,使尾数为24位,包含整数的躲藏位。
③把成果数据处理为32位契合IEEE浮点数规范的成果。包含1位符号位,8位成果阶码位,成果23尾数位。
332位浮点乘法器的完结与仿真
图4列出本规划的FPGA仿真成果。图中data1是被乘数,data2是乘数,reset是清零信号,高有用。start是开端信号,也是高有用。dataout10是两个浮点32位数相乘,进行规范化今后的成果,是一个32位数。Product是24位尾数相乘的成果,是一个48位数。
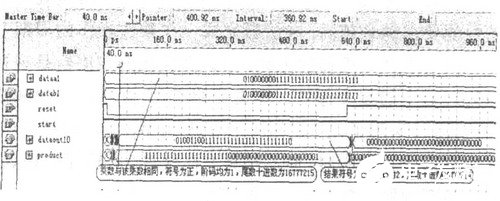
图432位浮点乘法器的仿真成果
整个规划选用了VHDL和VerilogHDL言语进行结构描绘,假如选用的是上华0.5的规范单元库,并用SynopsysDC进行逻辑归纳,其成果是完结一次32位浮点乘法的时刻为30ns,假如选用全定制进行后端地图布局布线,乘法器功能将愈加优胜。
4结语
本文给出了32位浮点乘法器的规划,浮点算法具有高精度性以及较宽的运算规模,使得乘法的规划更可以满意工程和科学核算的要求,电路的规划、模仿和完结均选用AlteraQuartusII4.1开发工具。选用的器材EPF10K100EQ240-1,逻辑单元是1914个,PIN的数量是147,本规划选用了一系列的算法和结构,如选用Booth编码的办法和Wallace树的结构,使得体系具有高速度特色,而且易于AS%&&&&&%的后端地图完结。
责任编辑:gt