ADI:在仅有零点电阻和电容可调理的情况下规划PLL滤波器

文章转自ADI官网，版权归属原作者一切

简介

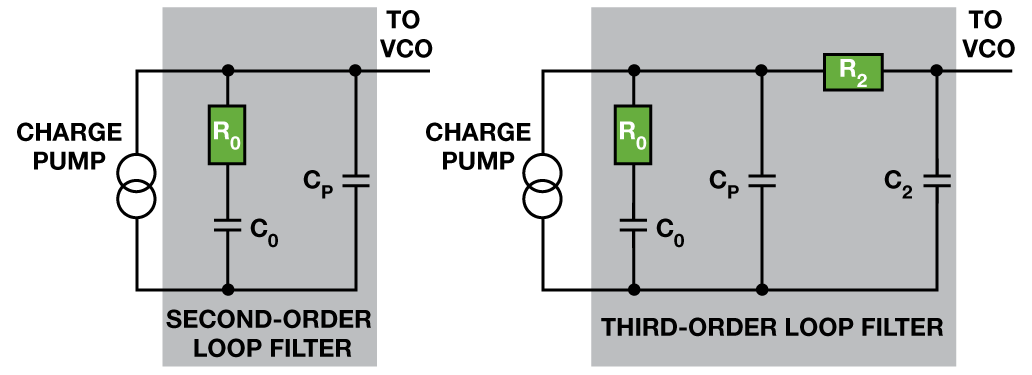
如参阅文献中所描绘，可选用规范进程来确认锁相环(PLL)中二阶环路滤波器的R₀、C₀ 和C_P 数值。它选用开环带宽(ω₀)和相位裕量(ϕM)作为规划参数，并可扩展至三阶环路滤波器，然后确认R₂ 和C₂（图1）。该进程可直接解出C_P，然后推导出其他数值。

2 或许是集成在PLL内的固定值元件，因而仅有R₀ 和C₀ 用来操控环路呼应。这便使得上述进程无效，因为无法调理C_P。本文提出一种替代进程，可在C_P 数值固守时运用，打破了无法操控C_P 值构成的约束。

假定条件

本环路滤波器规划办法依据两个假定，在三阶无源滤波器规划中，通过调理R₀ 和C₀ 来补偿R₂ 和C₂，能够将一个二阶环路滤波器规划扩展为三阶规划，此刻通常会选用这两个假定条件。

1. R₂ 和C₂ 构成的极点频率应当至少比ω₀（所需开环单位增益带宽）大一个数量级；f₀ ≤ 0.1/(2πR₂C₂)，其间f₀ = ω0/(2π)。
2. R₀-C₀-C_P 网络的R₂ 和C₂ 串联组合的负载可忽略不计。

二阶环路滤波器的传递函数

二阶环路滤波器有两个时间常数（T₁ 和T₂）与元件有关：

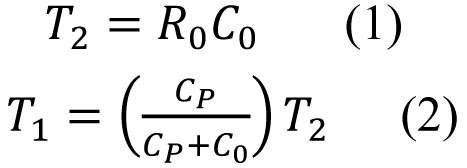
环路滤波器传递函数的T₁、T₂ 和C_P 很重要，因为它关于PLL 的全体呼应起着很大的效果：

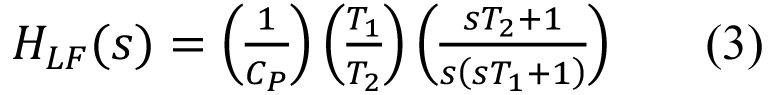
PLL体系函数

图2 中的小信号模型为PLL呼应的等式化供给了一种途径，并为剖析输入端相位搅扰所构成的输出端相位改变供给了模板。留意，压控振荡器(VCO)作为一个频率源，表现为抱负的相位积分器，因而其增益(K_V)系数为1/s（对积分进行等效拉普拉斯改换）。因而，PLL的小信号模型是复频率s的函数（s = σ + jω）。

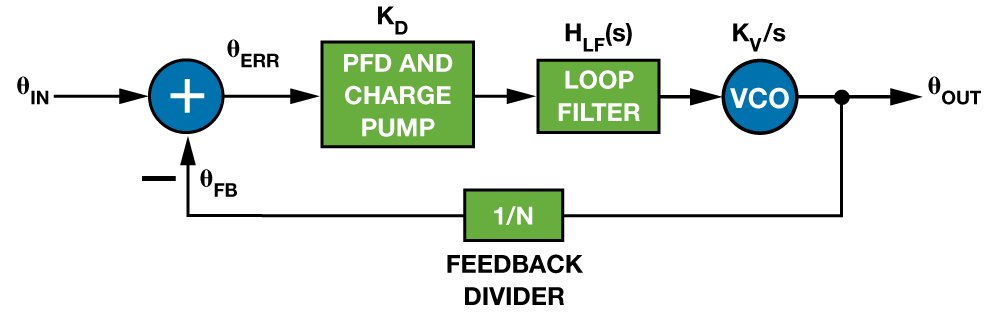
PLL的闭环传递函数(H_CL)界说为：θ_OUT/θ_IN。开环传递函数(H_OL)界说为：θ_FB/θ_IN，与闭环传递函数相关。主张以H_OL 来标明H_CL，因为开环传递函数包括闭环安稳性的头绪：

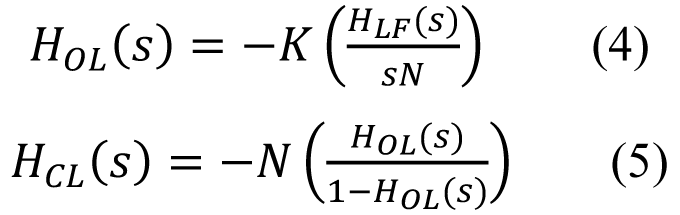
K 标明鉴频鉴相器(PFD)、电荷泵和VCO的组合增益——也就是说，K = K_DK_V，其间K_D 标明电荷泵电流，单位为A；K_V 标明VCO增益，单位为Hz/V。H_OL、H_CL 和H_LF 均为s 的函数。等式4 中的负号标明图2 中求和节点的负反馈导致相位回转。依据等式4 界说的HOL导致等式5 中分母的减法运算，直观地解说了闭环安稳性。

查看等式5，能够发现潜在的环路安稳性问题。因为H_OL 是复数频率s = σ + jω的函数，它必定具有取决于频率的起伏和相位重量。因而，关于恣意的s 值，假如H_OL 一起表现出单位增益和零点相移特性（或2π 弧度的整数倍），则H_CL 分母为零，闭环增益再次变为未界说，体系变得极不安稳。这意味着安稳性受依赖于频率的H_OL 起伏和相位特性所操控。事实上，在使得H_OL 为单位起伏的频率处，H_OL 相位有必要脱离零（或脱离2π 恣意整数倍）满意远，才干防止等式5 中的分母为零。

使H_OL 为单位起伏处的频率ω₀ 十分重要。ω₀ 处的H_OL 相位决议了体系的相位裕量ϕ_M。ω₀ 和ϕ_M 都可由H_OL 推导得出。

依据ω₀ 和ϕ_M 界说R₀ 和C₀

0 和C₀
运用规划参数ω₀ 和ϕ_M 来确认R₀ 和C₀ 值要求表达式包括这四个变量，以及其它常数项。能够从等式4 下手，因为等式4 界说了H_OL。这样便将H_LF 参加其间，然后通过T₁ 和T₂ 参加R₀ 和C₀。因为H_OL 具有起伏和相位，因而原则上ω₀ 和ϕ_M 也能参加其间。将等式3 代入等式4，从头排列各项可得等式6；等式6 以T₁ 和T₂ 以及常数K、N 和C_P 来标明H_OL：

将等式3 代入等式4，从头排列各项可得等式6；等式6 以T₁ 和T₂ 以及常数K、N 和C_P 来标明H_OL：

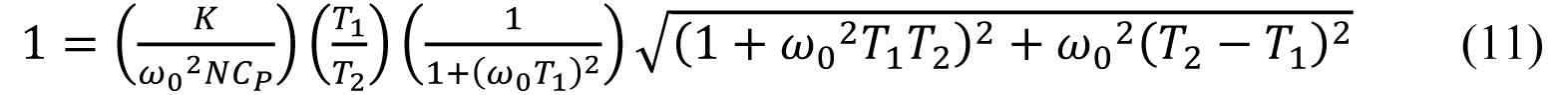
在s = jω 时进行评价，可得H_OL 频率呼应如下：

分母中的(jω)² 项可简化为–ω2：

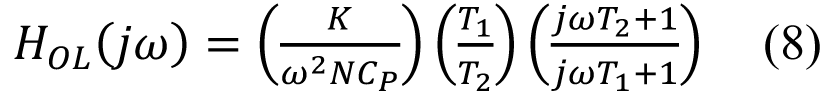
H_OL 起伏和相位为：

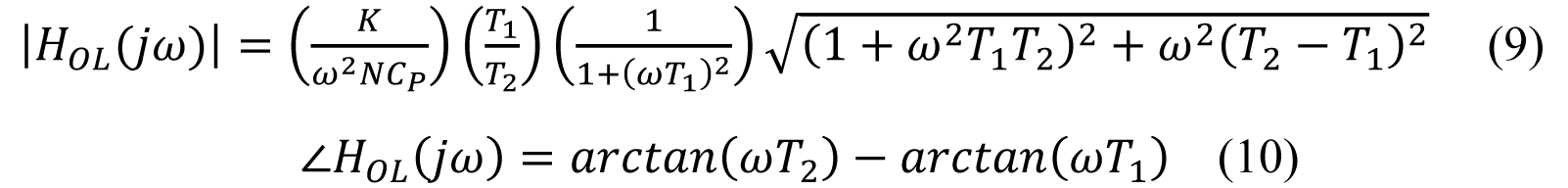
记住，T₁ 和T₂ 是R₀、C₀ 和C_P 代数组合的缩写表达式。ω = ω₀ 时评价等式9，并使|H_OL| = 1 即可界说单位增益频率ω₀，标明H_OL 为单位起伏时的频率。

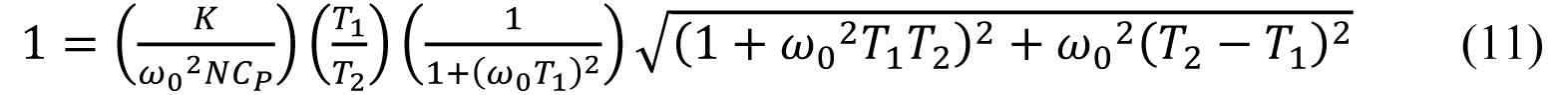
类似地，ω = ω₀ 时评价等式10，并使∠H_OL = ϕ_M 即可界说相位裕量ϕ_M，标明频率为ω₀（单位增益频率）时的H_OL 相位。

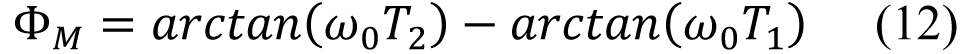
扩展等式11 和等式12 很简单，将等式1 中的T₂ 和等式2 中的T₁ 代入即可将R₀ 和C₀ 带入等式。因而，咱们顺畅地将ω₀ 和ϕ_M 与变量R₀ 和C₀ 以及常数K、N 和C_P 相关联。

一起求解咱们所得到的等式中的R₀ 和C₀ 很困难。MathCad^®供给的符号处理器可求解这两个联立方程，但有必要以arctan 替代arccos。进行改换后，符号处理器便可求解R₀ 和C₀，得到下列解集（R_0A、C_0A；R_0B、C_0B；R_0C、C_0C；以及R_0D、C_0D）。有关对等式12 进行改换以便运用arccos 函数的详细信息请拜见附录。

这个成果是有问题的，因为方针是在给定ω₀ 和ϕ_M 的情况下求解R₀ 和C₀；而运算成果标明存在四对或许的R₀ 和C₀，而非仅有的R₀、C₀ 对。可是，若进一步查看这四组成果，便可得出只需一组解。

留意，就PLL 建模而言，上述等式中的一切变量都具有正值，包括cos(ϕ_M)；这是因为，ϕ_M 的规模约束在0 和π/2 之间。因而，C_0A和R_0B 显然是负数。由此可知，R_0A、C_0A 和R_0B、C_0B 可当即加以扫除，因为元件值不或许为负，但需进一步剖析R_0C、C_0C 和R_0D、C_0D。

留意，包括R_0C、C_0C 和R_0D、C_0D 在内的四个等式有公因数：

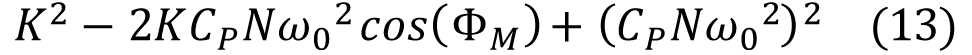
进一步剖析可知，等式13 的方法为：a² – (2ac)cos(β) + c ²。以b²标明该式，可得：

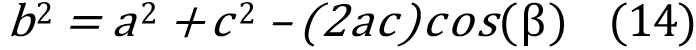
等式14 即为余弦定理，以a、b 和c 标明三角形的三条边长度，β标明极点对边b 的内角。因为b² 标明三角形一条边长度的平方，它有必要为正，这也就意味着等式14 的等号右边也有必要为正。因而，等式13 有必要为正，意味着R_0D 的分母为正。R_0D 的分子相同为正，因而R_0D 有必要为负，这便扫除了R_0D、C_0D。这使得仅有R_0C、C_0C对可作为等式11 和等式12 的解。

R₀ 和C₀ 的约束

尽管等式15 和等式16 有或许是等式11 和等式12 的公共解，但它们仅在R₀ 和C₀ 均为正时才有用。仔细查看R₀ 可知其为正——它的分子为正，因为cos2(x)规模为0 到1，且它的分母与等式13相同，由前文可知其为正。C₀ 分子相同与等式13 相同，因而只需分母满意下列条件，C₀ 就为正：

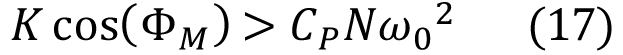
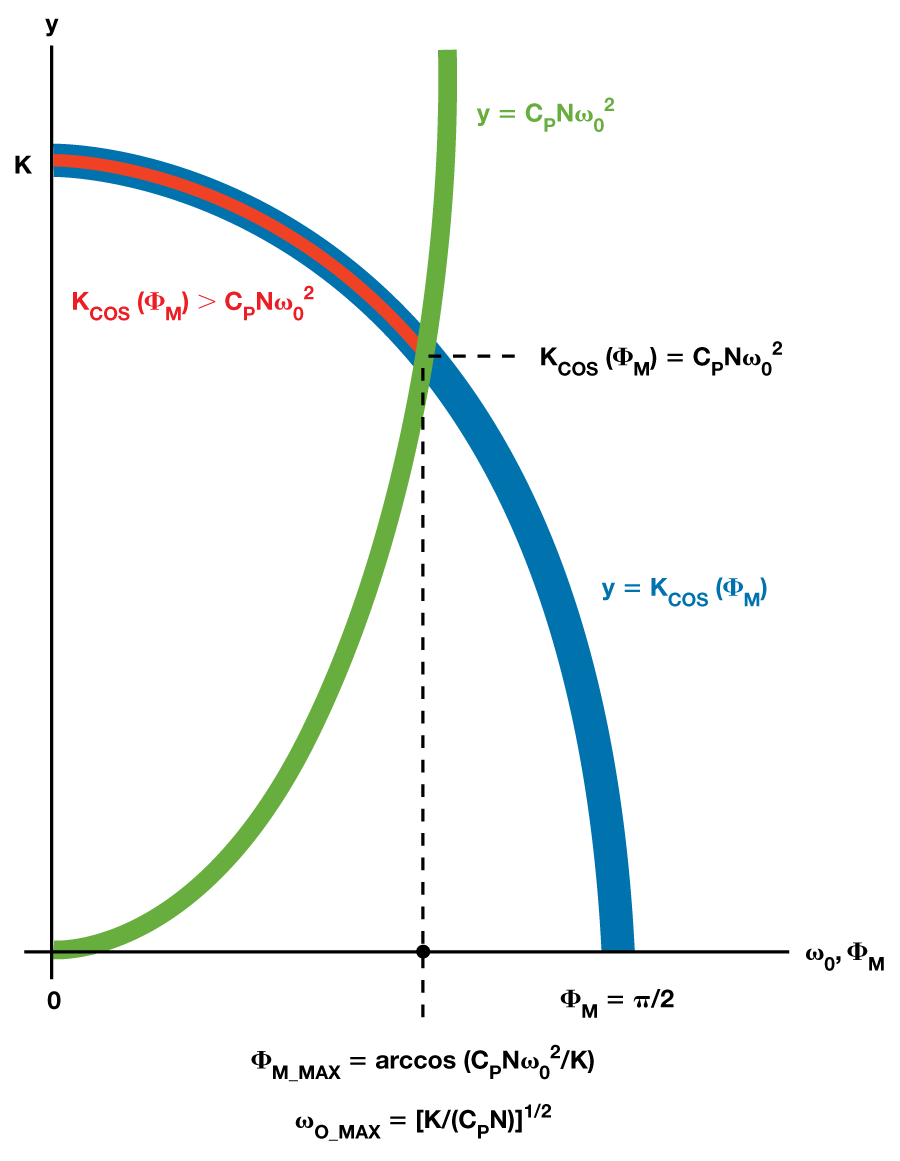
图3 以图形方法标明这种联系；不等式17 左右两边均等于y（蓝色曲线和绿色曲线），水平轴同享ω₀ 和ϕ_M。两条曲线的交点标明ω₀ 和ϕ_M 的鸿沟。赤色弧线部分所标明的条件使等式17 建立。赤色弧线下方的水平轴部分决议了C₀ 为正的ϕ_M 和ω₀ 规模。留意，蓝色曲线和绿色曲线交点正下方水平轴上的点确认了ϕ_{M_MAX}，即ϕ_M 的最大值；该值确保C₀ 为正。

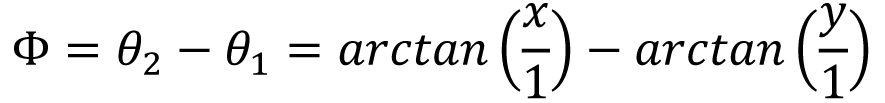
等式18 要求C_PNω₀² 小于K，才干满意ϕ_{M_MAX} 的arccos 规模为0到π/2 的约束条件。这便确认了ω_{0_MAX}，即ω₀ 的上限，确保C₀为正。

补偿R₂ 和C₂（三阶环路滤波器）

就三阶环路滤波器而言，R₂ 和C₂ 重量发生额定的相移Δϕ；该相移与二阶环路滤波器有关：

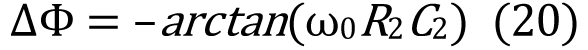
为了处理这个额定的相移，应将其从所需的ϕ_M 值中扣除。

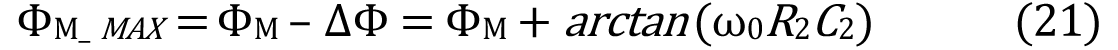
将ϕ_{M_NEW} 代入等式15 和等式16 可得到不同的R₀ 和C₀，然后针对二阶解，将新数值用来补偿R₂ 和C₂ 引进的额定相移。R₂ 和C₂ 的存在还会影响ϕ_{M_MAX}，即ϕ_M 的最大答应值。ϕ_M 新的最大值(ϕ_{M_MAX_NEW})为：

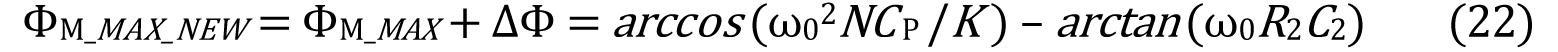
定论

本文演示了仅有R₀ 和C₀ 元件值可调理时，怎么运用开环单位增益带宽(ω₀)和相位裕量(ϕ_M)作为二阶或三阶环路滤波器的规划参数。选用R₀ 和C₀ 的二阶环路滤波器仿真PLL，成果与H_OL 以及由此得到的相位裕量理论值完美符合，然后验证了这些等式。依据等式19和等式18，参数ω₀和ϕ_M 针对二阶环路滤波器别离具有上限值。

确认R₀ 和C₀ 的进程中对二阶环路滤波器进行了假定，但通过将所需的相位裕量(ϕ_M)依据等式21 调理为新的值(ϕ_{M_NEW})便可扩展使用到三阶环路滤波器的规划中，然后依据等式22 得到一个新的上限值(ϕ_{M_MAX_NEW})。

尽管运用二阶环路滤波器进行仿真可验证等式15 和等式16，但若要验证将规划进程扩展至三阶环路滤波器的等式则需对环路滤波器呼应H_LF(s)进行从头界说，使其包括R₂ 和C₂，如下所示：

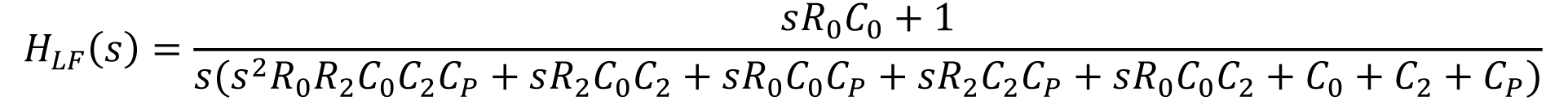
将HLF 的这种方法使用到H_OL 和H_CL 等式，便可运用R₀ 和C₀ 仿真三阶环路滤波器规划。对其进行仿真可知，当运用三阶环路滤波器时，由理论频率呼应和相位裕量推导而得的R₀ 和C₀ 核算值与PLL 的H_OL 有关。这首要是因为受到了三阶环路滤波器中H_OL的R₂ 和C₂ 影响。

如前所述，R₀ 和C₀ 等式假定为运用二阶环路滤波器，但在二阶滤波器中不存在R₂ 和C₂，因而尽管通过调理R₀ 和C₀ 能够补偿R₂和C₂ 构成的相移，可是将它们看做二阶环路滤波器的一部分仍是会构成一个差错源。可是，哪怕存在这样的差错，仿真成果也标明，运用通过调理的R₀ 和C₀ 值，但将ω₀ 约束在最高为等式19推导成果的¼也能取得令人满意的成果。事实上，仿真开环带宽和相位裕量的成果标明，运用三阶环路滤波器的PLL，其与规划参数（ω₀ 和ϕ_M）的差错很小。

仿真成果

以下为针对三阶环路滤波器PLL 运转四次仿真的成果。一切仿真均选用下列固定环路滤波器元件和PLL 参数：

C_P = 1.5 nF

R₂ = 165 kΩ

C₂ = 337 pF

K_D = 30 µA

K_V = 3072 (25 ppm/V at 122.88 MHz)

N = 100

仿真1 和仿真2 运用ω₀ = 100 Hz，该值挨近124.8 Hz 的核算上限值(ω_{0_MAX})。因而，仿真1 和仿真2 违背规划参数值（ω₀ 和ϕ_M）约10%。另一方面，仿真3 和仿真4 运用ω₀ = 35 Hz，约为上限值的¼。与预期相一致，仿真3 和仿真4 十分挨近规划参数（ω₀和ϕ_M），差错仅为1%左右。

表1 汇总了仿真成果，并包括了给定规划参数ω₀ 和ϕ_M 的R₀、C₀、ω_{0_MAX} 和ϕ_{M_MAX} 核算值。留意，为了便利进行比照，主张仿真1和仿真3 都运用ϕ_M = 80°，但仿真1 有必要满意等式22 的约束条件，即ϕ_M < 48°（因而，挑选42°）

表1：仿真成果汇总

	仿真1		仿真2		仿真3		仿真4
参数	ω0	ϕM	ω0	ϕM	ω0	ϕM	ω0	ϕM
规划	100 Hz	42°	100 Hz	30°	35 Hz	80°	35 Hz	30°
仿真	93.1 Hz	38.7°	92.5 Hz	27.1°	34.9 Hz	79.0°	34.7 Hz	29.3°
R0	969.6 kΩ		1118 kΩ		240.1 kΩ		139.9 kΩ
C0	14.85 nF		3.670 nF		225.5 nF		21.24 nF
ω0_MAX	124.8 Hz		124.8 Hz		124.8 Hz		124.8 Hz
ϕM_MAX	48.0°		48.0°		84.8°		84.8°

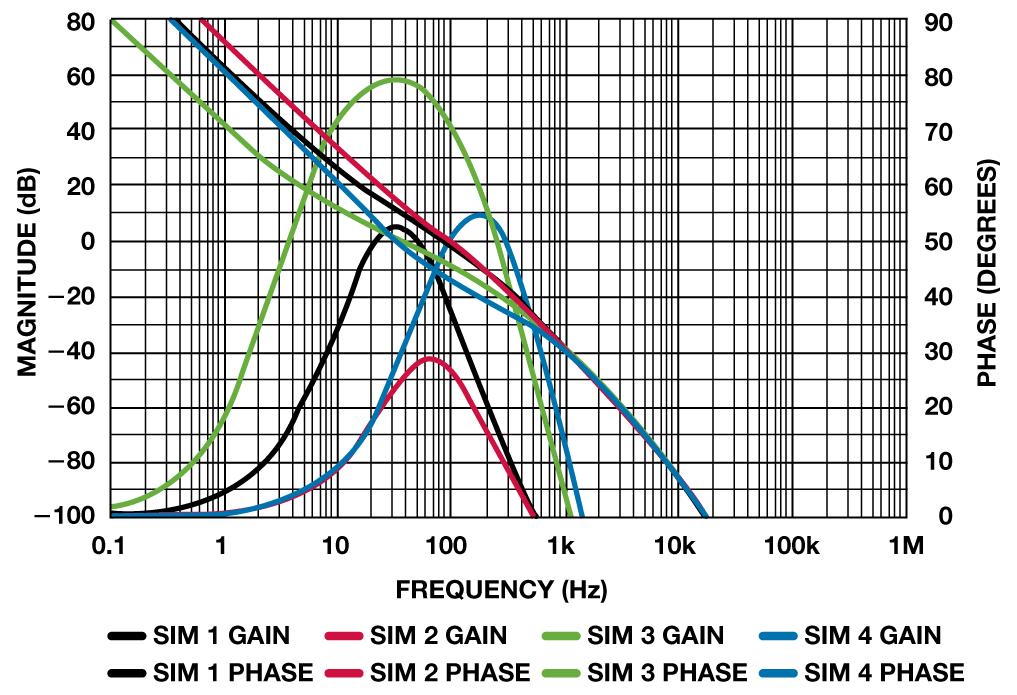
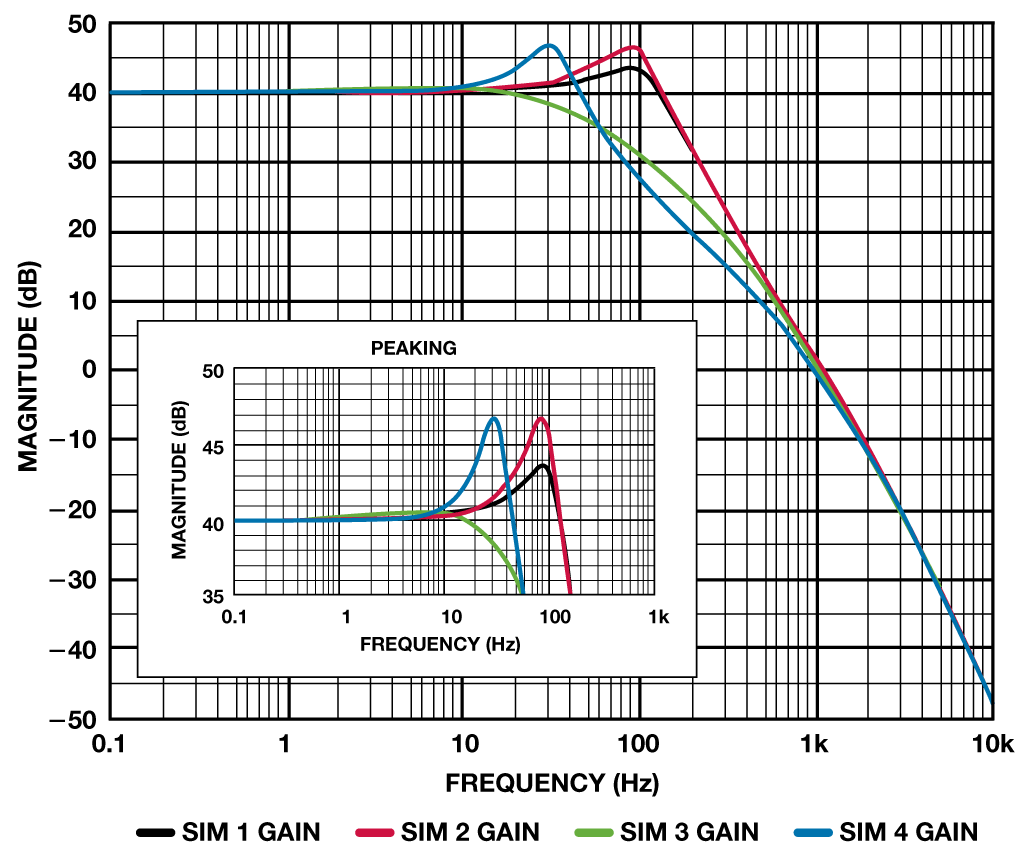
图4 和图5 显现各仿真的开环和闭环呼应。

附录—将非接连Arctan 函数转换为接连Arccos 函数

等式10 演示了视点ϕ 等于视点θ₂ 和视点θ₁ 之差，其间θ₂ =arctan(ωT₂)，θ₁ = arctan(ωT₁)。此外，ωT₂ 能够标明为x/1；ωT₁ 能够标明为y/1：

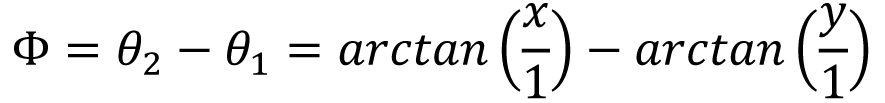
这标明两者之间存在如图6 所示的几许联系，其间θ₁ 和θ₂ 别离由图6 (b)和图6 (a)的三角形界说。图6 (c)结合了这两个三角形，标明ϕ等于θ₁ 和θ₂ 之差。

余弦定理将三角形的某个内角(θ)与三角形的三条边（a、b 和c）相关联，联系式如下：

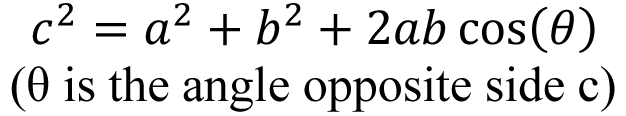
将余弦定理用在图6 (c)的ϕ 角，得到：

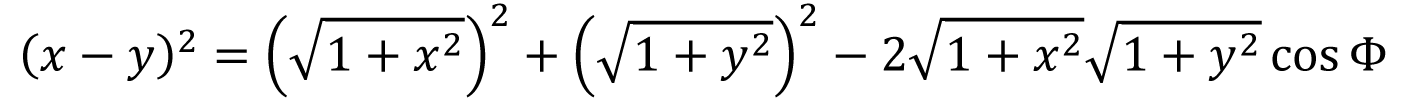
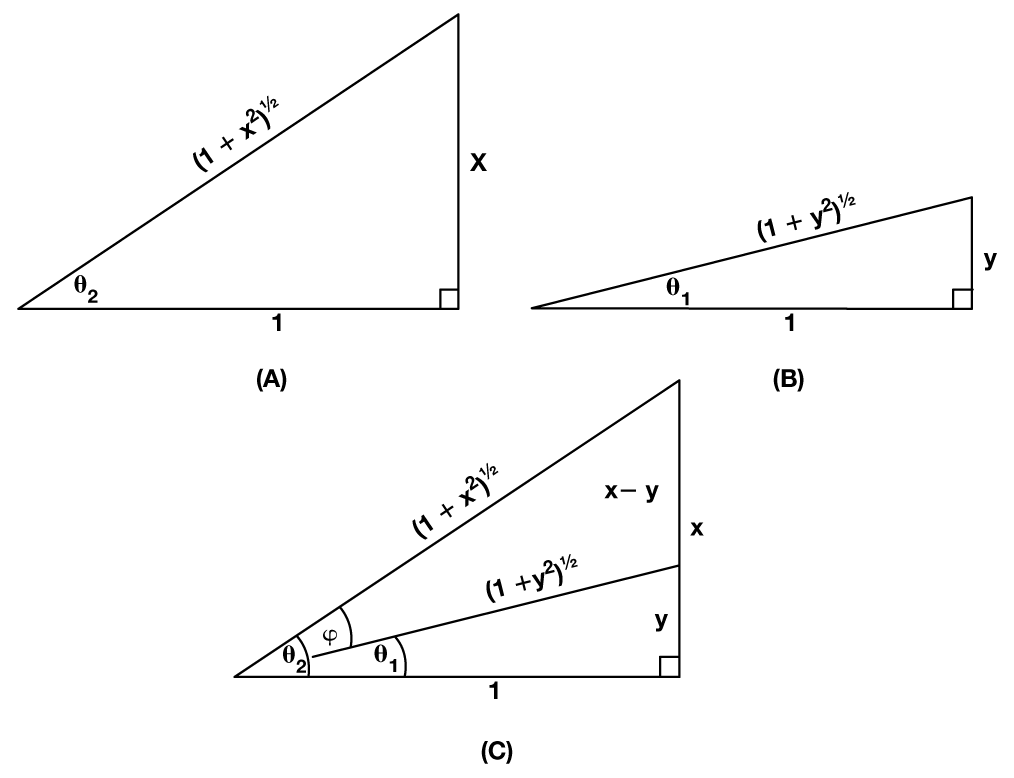
求解ϕ：

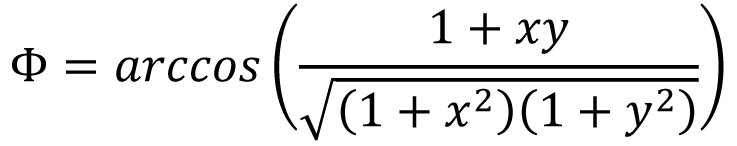
可是，因为x/1 = ωT₂ 且y/1 = ωT₁，因而可用T₁ 和T₂ 来标明ϕ。

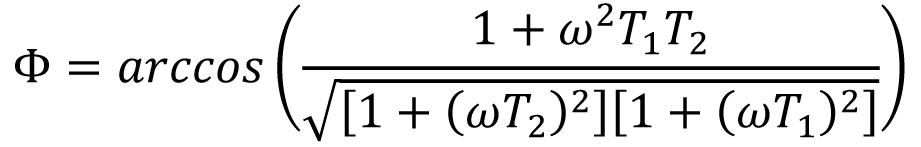
参阅电路

Brennan, Paul V. 锁相环：原理与实践. McGraw-Hill, 1996.

Keese, William O. AN-1001, National Semiconductor 使用笔记, 用于电荷泵锁相环的无源滤波器规划技能剖析与功能评价. 1996 年 5 月。

MT-086：锁相环(PLL)基本原理

PLL 与集成VCO的PLL