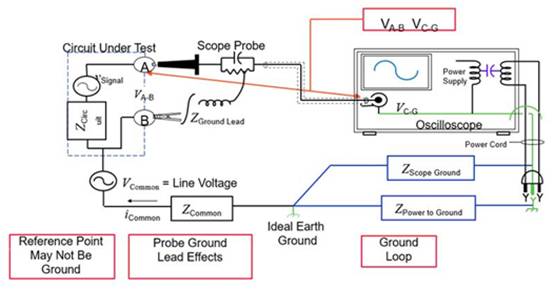
由传感器所检测到的奇特信号往往载有设备运转状况特征的重要信息。判别状况信号的奇特点出现时刻,并对信号奇特性完成定量描绘,在信号处理和故障确诊等范畴有着重要的含义。
信号的奇特性剖析是提取信号特征的重要手法,傅里叶改换一直是研讨信号奇特性的经典东西,可是由于傅里叶改换对信号的表明要么在时域,要么在频域,缺少空间部分特性,因而只能确认信号奇特性的全体信息,无法确认奇特点的空间散布。小波改换具有时-频部分化特性,能够有效地剖析信号的奇特性,确认奇特点的方位与奇特度的巨细,为信号奇特性剖析供给了有力的东西。
一 基本理论
(1) 小波剖析概略
小波剖析是自1986年以因由Meyer,Mallat及Daubechies等的研讨工作为根底而敏捷开展起来的一门新兴学科,他是傅里叶剖析(Fourier Analysis) 划时代的开展成果,是现在数学剖析和信号处理范畴中广泛运用的一套新理论、新办法,如:信号剖析、图画处理、量子力学、军事电子对抗与兵器的智能化、核算机分类与辨认、数据压缩、医学成像与确诊、地震勘探数据处理、边际检测、音乐与语音人工合成、大型机械的故障确诊、大气与海洋波的剖析、分形力学、流体湍流以及天体力学等。但以上大多数范畴的运用都能够归结为信号处理问题,故本文才要点介绍小波剖析在信号处理方面的运用。
在信号处理范畴,对原始信号进行改换,从改换的成果和过程中提取信号的特征,取得更多的信息,而这些信息是本来信号没有直接供给的(隐含的),现在,已经有许多改换运用于信号处理,最基本的是频域改换和时域改换,最了解的莫过于傅里叶改换(Fourier Transform),可是,傅里叶改换只能分别对信号的时域和频域进行调查,不能把二者有机地结合起来。为了处理此问题,引入了短时傅里叶改换(Short-TIme Fourier Transform),该改换能够给出信号的时刻和频率的二维散布,在短时傅里叶改换中,其窗口宽度是一个稳定的值,不能根据信号部分特征调整其窗口宽度。为此,引入了小波改换,处理了以上问题。
小波剖析办法是一种窗口巨细(即窗口面积)固定但其形状可改动、时刻窗和频率窗都可改动的时频部分剖析办法。即在低频部分具有较高的频率分辨率和较
低的时刻分辨率,在高频部分具有较高的时刻分辨率和较低的频率分辨率,所以被誉为数学显微镜。在大标准下,能够将信号的低频信息(大局)表现出来,在小标准下,能够将信号的高频(部分)特征反映出来。 (2) 信号奇特性的有关界说
数学上称无限次可导函数是润滑的或没有奇特性,若函数在某处有接连或某阶导数不接连,则称函数在此处有奇特性,该点便是奇特点。信号的骤变点往往包括重要的信息。宇宙射线和太阳黑子迸发,空间核磁暴,关于在太空飞行的卫星和飞船安全构成严重要挟,影响太空飞行器的运用寿命。经过处理收集的空间数据,检测到奇变点,找到太空气候异动的时刻,做出科学的判别,及时调整飞行器姿势,以维护飞行器的安全。寻觅改变周期,总结规则,可为进行太空气候预报供给根据。
假定一维信号s(t)=s0(t)+n(t),n(t)为噪声。s0(t)在t的某一邻域内二阶可导,
一阶导数‘
0()St的极值代表了在极值某一相邻区间内,信号线性改变最剧烈的时刻。咱们往往对信号改变最剧烈的时刻,也便是’0()St的模‘0()St最大值地点时刻感兴趣。’0()St极值点对应于s0(t)的拐点。s0(t)的拐点对应于二阶导数‘’0()St的零点方位。‘’0()St的零点纷歧定是‘0()St的极值点。经过’‘0()St的零点方位以及零点邻域内值的正负性质,能够判别出s0(t)改变的凹凸特性,也能够判别该点是否是’0()St在某一邻域内的极值(极大值或极小值)。可是‘0()St的极小值并纷歧定成为’0()
St的最大值。
二 小波剖析根底


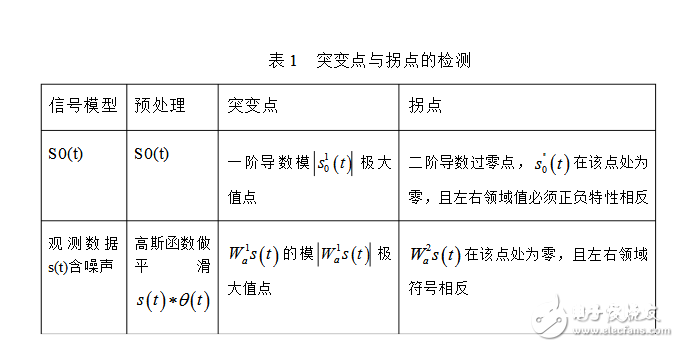
从以上剖析,用观测信号的滑润版别stt替代原信号s0(t)、1Wst和2Wst替代s0(t)的一阶和二阶导数进行剖析。表1比较了含有噪声的信号和不含噪声骤变点和拐点的差异。为了使成果更准确,归纳考虑1Wst和2Wst多标准核算的成果,来判别信号的骤变点
三 仿真试验与成果剖析
当小波函数可看作某一滑润函数的一阶导数时,信号小波改换模的部分极值
点,对应于信号的骤变点;当小波函数可看作某一滑润函数的二阶导数时,信号小波改换的过零点应于信号的骤变点。因而,选用小波改换模的过零点和部分极值点的办法能够检测信号的骤变点。比较来说,用部分极值点的办法进行检测更具优越性。
一般信号奇特性分为两种状况:①信号在某一时刻其幅值发作骤变,引起信号的不接连,这种类型的骤变称为第一种类型的接连点;②信号外观上很润滑,幅值没有发作骤变,可是信号的一阶微分有骤变发作且一阶不接连,这种类型的骤变称为第二种类型的接连点。
运用小波剖析能够检测出信号中骤变点的方位、类型以及改变的起伏。下面的比如将介绍用小波剖析检测第一类接连点,信号幅值改变的准确时刻,即接连点的准确方位。在这个比如中信号的不接连是由于低频特征的正弦信号在后半部分忽然参加高频特征的正弦信号的原因,剖析的意图是将参加高频特征的正弦信号的时刻检测出来。在MATLAB的指令窗口拟进行如下编程:
load freqbrk; %装载文件名为freqbrk的信号


该程序是用db(Daubechies)小波对信号第一类接连点进行剖析,成果如下:
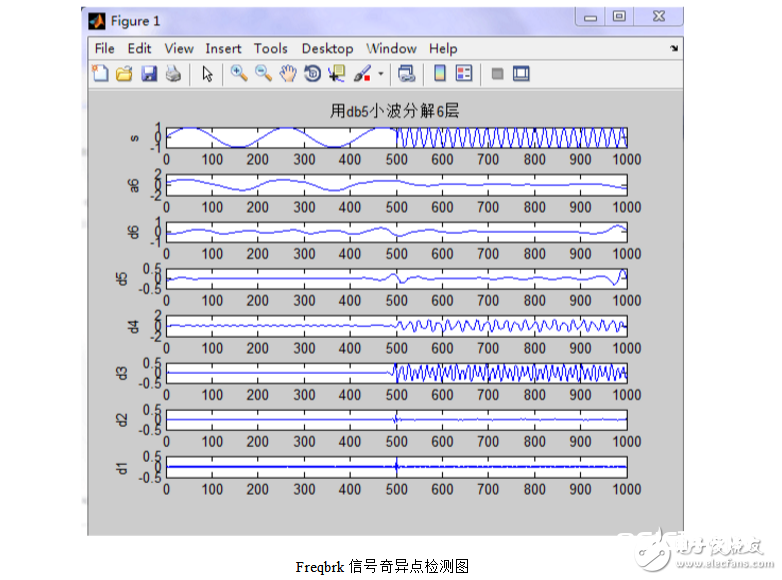
从成果波形图上能够看出,信号的不接连点在500t。运用db6小波将信
号进行6层分化,来检测第一种类型的接连点,能够十分清楚地调查到信号的不接连点,即高频特征的正弦信号的参加点,这是由于接连点包括了高频信息。假如只需求辨认第一种类型的接连点,则能够十分清楚地调查到信号的不接连点,即高频特征的正弦信号的参加点,这是由于接连点包括了高频信息。假如只需求辨认信号的不接连点,用db1小波比用db6小波作用好。
原始信号是由两个独立的满意指数方程的信号在t=500处连接起来的,因而它看上去是润滑的,但它的一阶微分有骤变。选用db6小波对信号分化后,在信号的第一层高频系数d1中能够显着的看到t=500的接连点。要留意的是,在信号奇特点的检测中,挑选小波的正则性十分重要,由于这时小波可完成一个长的冲
激呼应滤波器。
四 结束语
从实践数据的图形成果,可看出:2Wst的成果能够准确认位拐点,可是拐点纷歧定是骤变点,只要表现为凸特性的拐点才是骤变点;而骤变点一定是拐点。1Wst和1Wst是很难准确认位骤变点的方位,可是能够判别拐点是否为骤变点。所以,要归纳考虑1Wst和2Wst在标准上的核算成果,2Wst用于准确认位拐点(辨别凸性的拐点),而1Wst和1Wst用于判别该拐点是否是模极大,是否是骤变点。这样既能够确保成果稳健,又能准确认位奇特点的方位。 信号奇特点可经过信号的小波改换部分极大值来定位,而奇特性运用该点的Lipschitz α来定量描绘。运用该理论来完成信号的奇特性检测,比惯例手法更优越。需求留意的是:挑选不同的小波剖析信号的奇特性及奇特性方位和奇特度的巨细,其检测作用也纷歧样,因而,挑选适宜的小波十分重要。