热敏电阻的根本特性具体介绍
电阻-温度特性
热敏电阻的电阻-温度特性可近似地用式1表明。
(式1) R=Ro exp {B(I/T-I/To)}
| R | : 温度T(K)时的电阻值 |
| Ro | : 温度T0(K)时的电阻值 |
| B | : B 值 |
| *T(K)= t(ºC)+273.15 | |
但实际上,热敏电阻的B值并非是稳定的,其改变巨细因资料构成而异,最大乃至可达5K/°C。因而在较大的温度范围内运用式1时,将与实测值之间存在必定差错。
此处,若将式1中的B值用式2所示的作为温度的函数核算时,则可下降与实测值之间的差错,可以为近似持平。
(式2) BT=CT2+DT+E
上式中,C、D、E为常数。
别的,因生产条件不同形成的B值的动摇会引起常数E发作改变,但常数C、D 不变。因而,在讨论B值的动摇量时,只需考虑常数E即可。
• 常数C、D、E的核算
常数C、D、E可由4点的(温度、电阻值)数据 (T0, R0). (T1, R1). (T2, R2) and (T3, R3),通过式3~6核算。
首先由款式3依据T0和T1,T2,T3的电阻值求出B1,B2,B3,然后代入以下各款式。

• 电阻值核算例
试依据电阻-温度特性表,求25°C时的电阻值为5(kΩ),B值误差为50(K)的热敏电阻在10°C~30°C的电阻值。
• 步 骤
(1) 依据电阻-温度特性表,求常数C、D、E。
To=25+273.15 T1=10+273.15 T2=20+273.15 T3=30+273.15
(2) 代入BT=CT2+DT+E+50,求BT。
(3) 将数值代入R=5exp {(BTI/T-I/298.15)},求R。
*T : 10+273.15~30+273.15
• 电阻-温度特性图如图1所示
所谓电阻温度系数(α),是指在恣意温度下温度改变1°C(K)时的零负载电阻改变率。电阻温度系数(α)与B值的联系,可将式1微分得到。
![]()
这儿α前的负号(-),表明当温度上升时零负载电阻下降。
散热系数 (JIS-C2570)
散热系数(δ)是指在热平衡状态下,热敏电阻元件通过本身发热使其温度上升1°C时所需的功率。
在热平衡状态下,热敏电阻的温度T1、环境温度T2及耗费功率P之间联系如下式所示。

产品目录记载值为下列测定条件下的典型值。
| (1) | 25°C停止空气中。 |
| (2) | 轴向引脚、经向引脚型在出厂状态下测定。 |
额外功率(JIS-C2570)
在额外环境温度下,可接连负载运转的功率最大值。
产品目录记载值是以25°C为额外环境温度、由下式核算出的值。
(式) 额外功率=散热系数×(最高运用温度-25)
最大运转功率最大运转功率=t×散热系数 … (3.3)
这是运用热敏电阻进行温度检测或温度补偿时,本身发热发作的温度上升容许值所对应功率。(JIS中未界说。)容许温度上升t°C时,最大运转功率可由下式核算。
指在零负载状态下,当热敏电阻的环境温度发作急剧改变时,热敏电阻元件发作开始温度与终究温度两者温度差的63.2%的温度改变所需的时刻。
热敏电阻的环境温度从T1变为T2时,通过时刻t与热敏电阻的温度T之间存在以下联系。
| T= | (T1-T2)exp(-t/τ)+T2……(3.1) |
| (T2-T1){1-exp(-t/τ)}+T1…..(3.2) |
常数τ称热呼应时刻常数。
上式中,若令t=τ时,则(T-T1)/(T2-T1)=0.632。
换言之,如上面的界说所述,热敏电阻发作初始温度差63.2%的温度改变所需的时刻即为热呼应时刻常数。
通过时刻与热敏电阻温度改变率的联系如下表所示。


产品目录记载值为下列测定条件下的典型值。
| (1) | 停止空气中环境温度从50°C至25°C改变时,热敏电阻的温度改变至34.2°C所需时刻。 |
| (2) | 轴向引脚、径向引脚型在出厂状态下测定。 |
别的应留意,散热系数、热呼应时刻常数随环境温度、拼装条件而改变。
NTC负温度系数热敏电阻R-T特性

B 值相同, 阻值不同的 R-T 特性曲线示意图
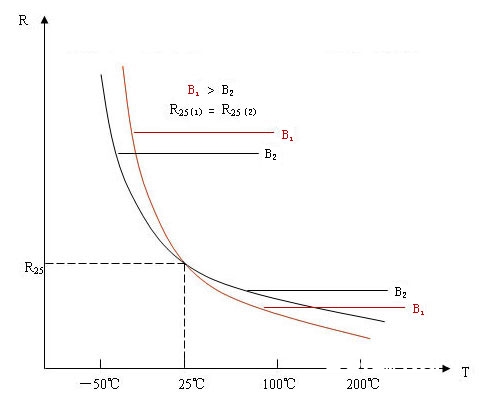
相同阻值,不同B值的NTC热敏电阻R-T特性曲线示意图