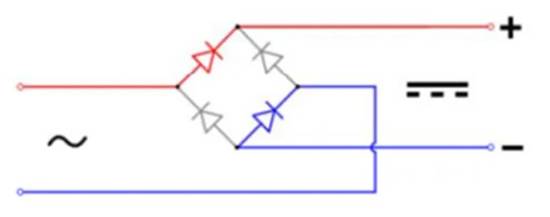
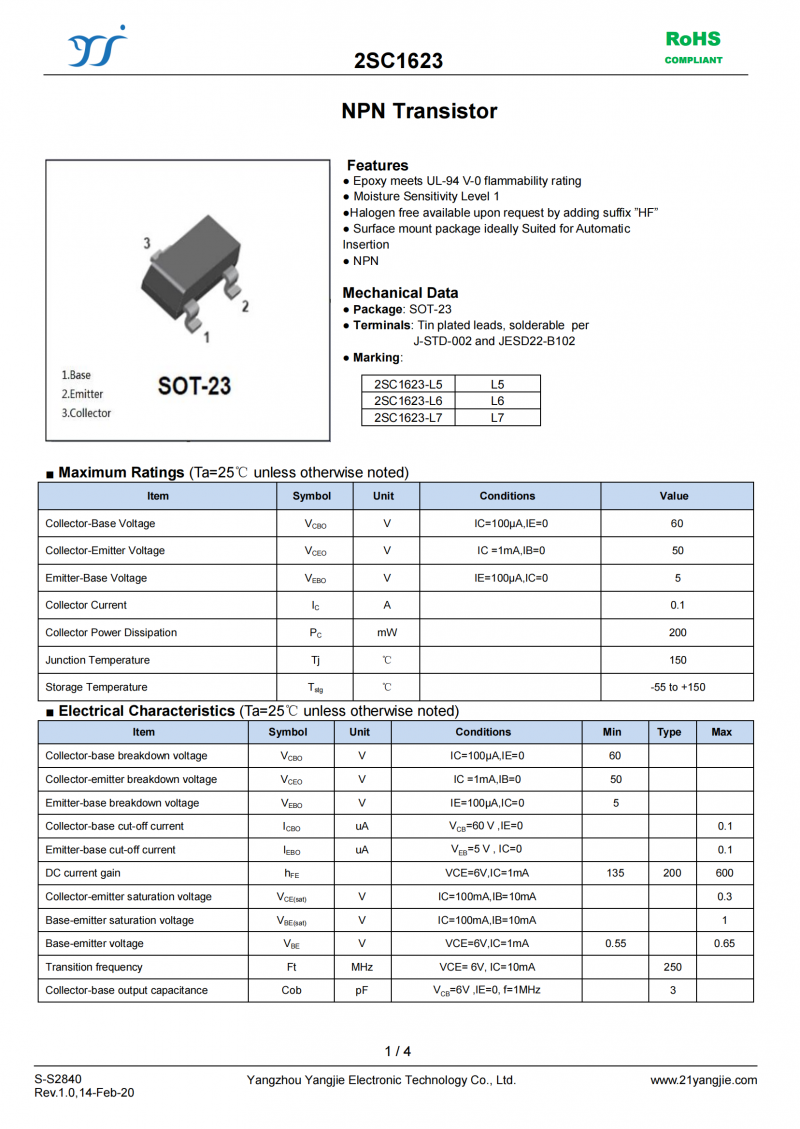
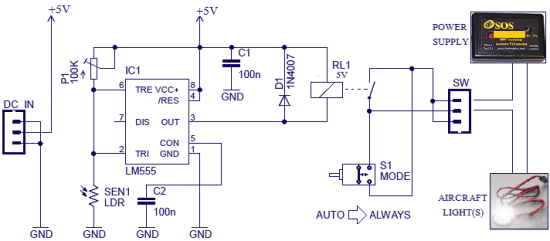
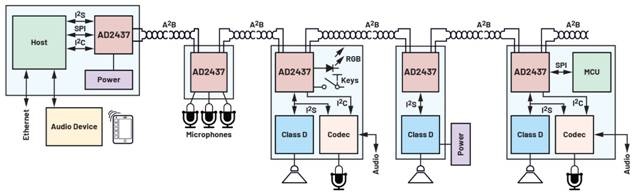
浮点型在内存中的存储散布办法因机器渠道而异,彻底了解一切机器渠道中的浮点型存储无疑是一件适当费事的事。走运的是,大多机器渠道都恪守 IEEE-754 规范,很或许读者和我运用的渠道正是运用的 IEEE-754 规范。
在C言语程序开发中,数值的处理是一门值得深究的科学。本文不行能将杂乱的数值算法以及相关的C言语程序开发经历逐个列出。事实上,评论怎么故抱负的数值精度进行核算,就和评论怎么编写最快的C言语程序,怎么规划一款优异的软件相同,首要取决于程序员自身的归纳本质。
鉴于此,这儿将测验介绍一些根底的,我以为每个C言语程序员都应该知道的内容。首要,咱们应该理解C言语程序开发中的两个浮点数何时持平。或许读者并不觉得难,由于好像C言语中的 == 运算符就能判别两个浮点数是否彻底持平。可是实际上,C言语中的 == 运算符是逐位比较两个操作数的,而两个浮点数的精度总是有限的,在这种场景下,== 运算符的实际运用含义就没有那么大了。
读者应该现已理解,核算机存储浮点数时,很有或许是需求放弃一些位的(假如该浮点数过长),假如 CPU 或许相应的程序没有依照预期四舍五入,那么运用 == 运算符判别两个浮点数是否持平或许会失利。例如,规范C言语函数库三角函数 cos() 的完成其实仅仅一种多项式近似,也便是说,咱们并不能盼望 cos(π/2) 成果的每一个位都为零。在C言语程序开发中,咱们乃至不能精确的表明 π。
假定在某段C言语程序中有两个数字 1.25e-20 和 2.25e-20,它俩的差值是 1e-20,远小于 EPSILON,可是明显它俩并不持平。可是假如这两个数字是 1.2500000e-20和1.2500001e-20,那么就能够以为它们是持平的。也便是说,两个数字间隔满足挨近时,咱们还需求重视需求匹配多少有用数字。
核算机存储空间总是有限的,因而数值溢出是C言语程序员最关怀的问题之一。读者应该现已知道,假如向C言语中的最大无符号整数加一,该整数将归零,令人溃散的是,咱们并不能只经过看这个数字的办法获悉是否有溢出发生,归零的整数看起来和规范零一模相同。当溢出发生时,实际上大多数 CPU 是会设置一个标志位的,假如读者懂得汇编,能够经过查看该标志位获悉是否有溢出发生。
float 浮点数溢出时,咱们能够便利的运用 +/- inf(无量)。+inf(正无量)大于任何数字,-inf(负无量)小于任何数字,inf+1 等于 inf ,依此类推。因而在C言语程序开发中,一个小技巧是,将整数转化为浮点数,这样就便利判别后续处理是否会形成溢出了。处理完毕后,再将该数转化回整数即可。

不过,将整数转化为浮点数判别是否溢出也是要付出代价的,由于浮点数或许没有满足的精度来保存整个整数。32 位的整数能够表明任何 9 位十进制数,可是 32 位的浮点数最多只能表明 7 位的十进制数。所以,假如将一个很大的整数转化为浮点数,或许不会得到希望的成果。此外,在C言语程序开发中,int 与 float 之间的数值类型转化,包含 float 与 double 之间的数值类型转化,实际上是会带来必定的功能开支的。
读者应该理解,在C言语程序开发中,不论是否运用整数,都应该当心防止数值溢出的发生,不仅仅是最开端和终究成果数值或许溢出,在一些核算的中心进程,或许会发生一些更大的值。一个经典的比如是“C言语数字配方”核算复数的起伏问题,极或许形成数值溢出的C言语完成是下面这样的:
假定该复数的实部 re 和虚部 im 都等于 1e200,那么它们的起伏约为 1.414e200,这确实在双精度的答应规模内。可是,上述C言语代码的中心进程将发生 1e200 的平方值,也即 1e400,这超出了 inf 的规模,此刻上面的完成函数核算的平方根将依然是无量大。
应该理解,上述C言语代码为了防止数值溢出,给出的完成实际上是一种近似。例如 im 等于 1e200,re 等于 1,那么 im/re 的平方依然能够到达 1e400,这会形成数值溢出。可是平方 re/im 却是能够的,由于 1e-400 会被四舍五入到零,满足挨近得到正确的答案。
走运的是,就像上面求复数起伏防止呈现数值溢出相同,防止两个挨近的数字相减呈现精度丢失的办法也是有的,可是并没有一个通用的办法。这儿给出一个简略的实例便是运用 1/x 的函数替代 x 的函数,这关于处理二次运算很有用。我的主张是,假如读者发现自己的C言语程序给出了令人置疑的数值,就应该查看一下相应的减法运算了。
看到这儿,信任读者应该想到C言语程序中的加法或许也有相同的问题:假定有数字 1.0,现在将其与 1e-20 相加。程序很或许以为 1e-20 很小,小于 EPSILON,所以疏忽它,得到答案 1.0。这实际上也是一种精度丢失。要彻底躲避C言语程序中的浮点数或许带来的问题,工作量无疑是巨大的。为了简化问题,咱们一般以为浮点数带来的精度问题是这样的:对浮点数的操作越多,丢失的精度也会越多。
正如前文举的比如 cos(π/2),C言语它的完成实际上是一种近似,得到的答案并不是 0,而是 6.12303E-17。不过就这个答案自身而言,它现已满足小,以为等于 0 也没什么大问题。可是假如咱们下一步核算是除以 1e-17,那么得到的答案就约是 6 了,这与预期的零相差甚远。
最终,在C言语程序开发中,并不是只要浮点数才重要的,整数相同重要,它的精确性是一个有用的东西。有时程序需求盯梢改变的分数(例如份额因子)。在这种情况下,已然浮点数受各种因素影响,那么咱们彻底能够将该分数存储为整数分子和分母来防止问题。在需求运用浮点数时,随时再做一次除法运算就能够了。