最基本的开关电容电路是由电子开关和电容组成的,首要应用是构成各种低通、高通、带通、带阻等开关电容滤波器(Switched-Capacitor Filter,SCF)。将开关电容电路与运算放大器结合,组成的开关电容有源滤波器具有许多独特的性质,但因为引入了电子开关,对电路特性进行紧密剖析变得反常困难,现在已有的剖析办法都仅仅在必定条件下从一个旁边面进行近似剖析,本文立足于最基本的电路理论,凭借核算机体系对其进行杂乱而严厉的剖析核算,终究得到了具有普遍意义的定论,上述文献的成果仅仅该普遍性定论的特例。
1 SCF电路
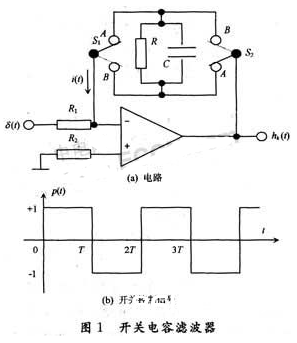
开关电容有源滤波器电路如图1(a),其间S1和S2是由周期为2T的方波信号操控的抱负电子开关,方波操控信号p(t)波形如图1(b),其占空系数为0.5。即在2kT
2 时域法特性剖析
时域剖析法的思路是依据图1的电路结构树立电路的微分方程(以输出电压为研讨目标)。转化周期为2T的电子开关的方波操控信号可标明为周期为2T的周期信号p(t)与单位阶跃信号ε(t)的乘积:
式中:k=0,1,2,…。fT=1/(2T)为开关频率,电路在k时段的时域呼应(输出电压)标明为hk(t),并设:
(1)电容C在t=0_时间电压为零(0_,kT_等带下划线符号标明相应时间的前瞬,下同),即:
(2)因为狄拉克δ函数鼓励下的零状况呼应h(t)的傅里叶改换即为电路的频率呼应函数,即体系(频谱)函数H(Ω),故设电路输入信号(鼓励)为δ函数,即:
因为电子开关周期性切换,RC电路对外电路的影响表现为:下一时段的输出电压初值是上一时段末时间输出电压值乘(-1),即:
图1(a)中抱负运放反相端为虚地,第0时段(即k=0,0≤t

由式(8)可见,第k段的非零值时区为(kT,(k+1)T_),即各时段非零值区间互不堆叠,对hk(t)关于k求和,得开关电容电路(对外)的单位冲激零状况呼应h(t)为:
特别注意,求和式是一周期为2T的周期方波p(t)与单位阶跃信号ε(t)的乘积,对上式取Fourier积分改换即得到开关电容电路体系频谱函数(用j标明虚数单位,下同):

也能够依据式(1)界说的周期为2T的开关方波信号p(t),将式(9)改写为:

易证式(13)与式(10)完全共同,故其幅频特性∣H(Ω)∣仍与式(11)相同。
3 频域法特性剖析
开关周期切换,构成的RC并联支路对外电路的等效电流ie(t)为:
上式阐明,Ie(Ω)是输入电流频谱I(Ω)周期延拓的组合,周期为Ω0=2π/T。各电流重量流过RC并联支路时的电压为相应电流重量与RC支路阻抗(R/(1+jωτ),ω=Ω(2n+1)π/T)的乘积,所以输出电压频谱U(Ω)为:
为求体系频谱函数,取i(t)=-ui(t)/R1=-δ(t)/R1,I(Ω)=-1/R1,得到体系频谱函数:

其间R/R1=τ/τ1,成果与式(14)共同,幅频特性∣H(Ω)∣仍与式(11)相同。
4 结 语
给定图1(a)电路参数τ和τ1,挑选α=τ/T别离取不同值时,依据式(11)做出的归一化幅频特性曲线如图2所示,结合对式(11)做深入剖析标明:
(1)α=τ/T较大时电路是梳齿崎岖按奇数倒数规则衰减的梳状滤波器,通带中心频率(梳齿)为:
此刻图1(a)电路答应f=fT,f=3fT,f=5fT,…等频率成份经过,且跟着频率的升高,输出崎岖按奇数倒数规则逐步减小。

(2)α=τ/T较大时,f=(2n)fT(其间n=0,1,2,…)是体系的阻带中心频率,落在这些频点上的信号将取得最小传输系数,最小传输系数(即梳状滤波器幅频曲线谷底高度)为:
(3)该梳状滤波器梳齿距离(即阻带中心频率或通带中心频率距离)为△f=2fT。
比较图2可看出:开关转化周期2T(相关于电路时间常数τ)越小,α越大,梳齿间谷底越挨近零,梳齿越尖利(即梳齿带宽越窄)。例如,核算发现:图2(a)中,α=τ/T=10,榜首梳齿通带宽度为B0.7=0.394fT。图2(b)中,α=τ/T=2,榜首梳齿通带宽度为B0.7=2.33fT。
(4)跟着电子开关切换周期2T增大(α减小),梳齿间谷底最小值逐步增大。电路逐步过渡为幅频特性曲线细微崎岖的低通滤波器,如图2(d)所示。低通滤波器传输函数极大值为:
由∣H(Ω)∣=0.707∣H(Ω)∣max能够求得低通滤波器上限截止频率,成果标明,关于低通滤波器.仍为α越大,低通滤波器上限频率(即带宽)越小。
责任编辑:gt









