导言
跟着人们生活水平的进步,对轿车舒适性的要求也越来越高。轿车空调的质量影响到对整车的点评。由于轿车是直接暴露在太阳或风雪下,并且轿车行进的速度改变无常,车内的空间有限。这都加大了轿车空调的规划难度。一般来说轿车空调由紧缩机,冷凝器,蒸发器,和胀大阀组成。轿车空调紧缩机是轿车空调的要害零部件,也是首要的运动部件。选用虚拟样机技能能够研讨轿车空调紧缩机的运动规矩和动力功能,为规划和优化供给协助。
虚拟样机技能是在产品的规划开发中,将涣散的零部件规划和剖析技能交融在一起,在核算机上建造出产品的全体模型,并对该产品在投入使用后的各种工况进行仿真剖析,猜测产品的全体功能,然后改善规划,进步产品质量。
本文是选用MSC.ADAMS 软件对一款轿车空调紧缩机进行运动,动力剖析,然后了解其运动规矩,并核算一些联接副的受力状况。
1 轿车空调紧缩机运动组织概述
轿车空调紧缩机可分为往复式和旋转式二大类。往复式的又分曲轴连杆式,轴向活塞式,和径向活塞式。其间轴向活塞式又分旋转斜盘式和摇晃斜盘式。旋转式又分刮片式,翻滚活塞式,三角转子式,涡旋式,螺杆式。本文首要研讨5 缸摇晃斜盘式的轿车空调紧缩机。
摇晃斜盘式的轿车空调紧缩机的作业原理是经过主轴的旋转带动斜盘的滚动,经过只能进行摇晃的行星盘将旋转运动转化为活塞的往复运动,活塞在气缸里对制冷剂进行紧缩。(见图1)

图1 空调紧缩机中心部件安装图
2 摇晃斜盘式紧缩机运动学几许联系
摇晃斜盘式紧缩机经过主轴带动斜盘作圆周运动,行星盘由于导向杆的运动束缚,将主轴的周转运动转化为斜盘外表质点的轴向往复,并经过连杆带动活塞,构成空间上类曲柄滑块组织。
本模型中,由于遭到行星盘上导向杆的束缚,活塞3 的连杆衔接行星盘一端的球心一直坐落轴线与导向杆轴线所确认的平面内,该活塞的运动处于较为特别的方位,几许联系为平面运动。其他活塞1,5,活塞2,4 互为对等联系,且均属空间运动学领域。
3 活塞运动学公式推导
在研讨紧缩机时,活塞的运动规矩十分重要。下面以活塞3 为例,对紧缩机的活塞质心运动进行公式推导。
如图2 所示,对该几许联系构建关闭矢量多边形,l1、l2、l3、s4 均为相应的杆矢量,θ1、θ2、θ3、θ4 为杆件的方位角,各杆件矢量方向不影响核算成果,但方位角均应由x 轴开端,并以沿逆时针方向计量为正。
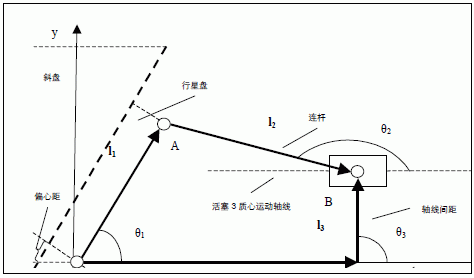
图2 活塞3 运动几许联系
由于主轴轴线(即斜盘轴线)和行星盘轴线各安闲作业结合面(粗虚线)上的交点有一偏疼距,其偏置的成果正好使得行星盘中心球状腔的球心(O 点)落在了主轴轴线(X 轴)上。
所以,在固定球轮的顶压下,行星盘彻底绕O 点作摇晃,行星盘中心孔腔的球心(O 点)到圆周孔腔(即连杆球铰链落位处)的球心(A 点)之间的间隔为曲柄长度,连杆两球心之间间隔为连杆长度,活塞质心运动状况等效B 点(球铰链球心)运动状况。
由于在关闭矢量多边形中,各矢量之和为零:
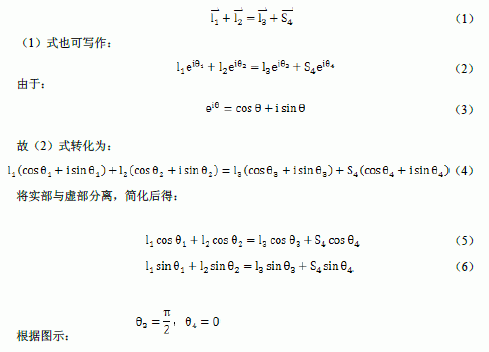
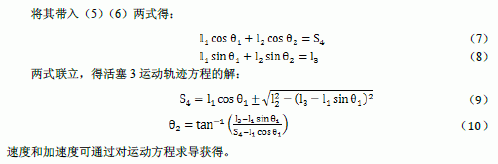
4 经过MSC.ADAMS 对紧缩机进行运动动力剖析
4.1 剖析的根本进程
轿车空调紧缩机的仿真进程如下:1. 运用UG 的三维实体建模模块对紧缩机中心运动组织进行三维建模,首要包含主轴、斜盘、行星盘、连杆和活塞五大部件,并在UG 环境下进行安装。2. 将建好的实体模型以Parasolid 格局输出,导入ADAMS 中,增加资料特点,并依据默许方位联系附加运动束缚,完结模仿运动无干与。3. 依据三种给定的不同工况,核算活塞端面的气体压力,将气体力学方程导入,完结力学束缚的增加。4. 依据工况,在驱动轴上赋给指定转速,输出动力学特性曲线,包含活塞质心位移曲线、活塞质心速度曲线、活塞质心加速度曲线和活塞端面力曲线。并对获取的数据进行动力学剖析。
4.2 零部件的物理参数
其几许参数和惯性参数选用三维CAD 实体建模软件UG-Ⅱ核算得到,如表1 所示。这对几许形状极不规矩,选用核算方法很难得到精确数值的物体,如斜盘等,将大大简化核算进程。
表1 空调紧缩中心部件力学参数
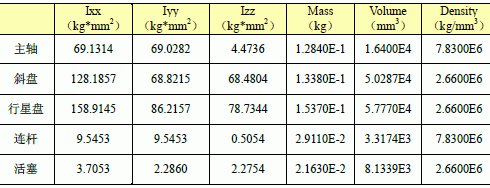
4.3 束缚的选定
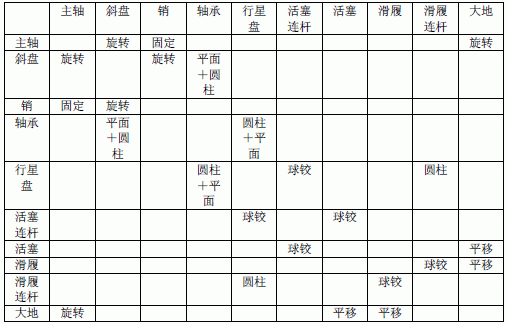
在ADAMS 的VIEW 模块对模型中的零件之间的运动副进行束缚界说。下表为运动副的束缚界说。
表2 空调紧缩中心部件运动束缚
4.4 确认边界条件(活塞压力的确认)
4.4.1 仿真工况:
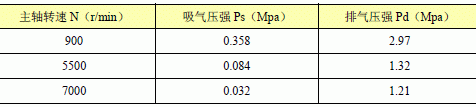
按实验要求,如表4.2.3-1 所示,仿真进程将在900rps、5500rps、7000rps 三种转速及各自相对应的吸气压强、排气压强下进行测验。
表3 空调紧缩机实验工况
4.4.2 活塞顶部压力公式推导:
依据气体方程:多变进程的 P*VN=C 得出:
紧缩进程:P1=Ps*((L+C)/( .5H11G.cm_dis+d3+C)) N
排气进程:P2=Pd
胀大进程:P3=Pd*(C/(.5H11G.cm_dis+d3+C)) N
吸气进程:P4=Ps
其间:
L=紧缩机均匀行程
C=余隙
N=多变指数
d3=活塞下止点均匀方位
.5H11G.cm_dis=活塞质心点方位
4.4.3 多变指数的确认
实践热机中,有些进程工质的状况参数p、v、T 等都有显着的改变,与外界之间换热量也不行忽略不计,这时它们不能简化为四种根本的热力学进程(定容、定压、定温文绝热)。实验测定了一些进程中1kg 工质的压力p 和v 的联系,发现它们挨近指数函数,用数学表达式描绘即:p*vn=定值。该式即多变进程的进程方程式。n 为多变指数,它能够是负无量到正无量之间的恣意数值。多变进程比前述几种特别进程更为一般化,但也并非恣意的进程,它仍依据必定的规矩改变:整个进程遵守进程方程p*vN=定值,n 为某必定值。
实践进程往往更为杂乱。比如柴油机气缸中的紧缩进程,开端时工质温度低于缸壁温度,边吸热边紧缩而温度升高,高于缸壁温度后则边紧缩边放热,整个进程n 大约从1.6 改变到1.2 左右;至于胀大进程,由于存在后燃及高温时被离解气体的复合放热现象,状况更为杂乱,其散热规矩的研讨已不归于热力学的规模。关于多变指数n 式改变的实践进程,若n 的改变规模不大,则可用一个不变的均匀值近似地替代实践改变地n;若n 地改变较大,则可将实践进程分成数段,每一段都近似为n 值不变。
本课题中,由于n 值的改变规模不大,依据以往实践工况和以往经历,选取n=1.3。
如图3 所示,紧缩和胀大为多变进程,多变指数n=1.3。胀大完毕点A 的压力应小于吸气压力Ps,紧缩完毕点B 的压力应大于排气压力Pd,但考虑影响有限,故胀大完毕点A 的压力=Ps,紧缩完毕点B 的压力=Pd。
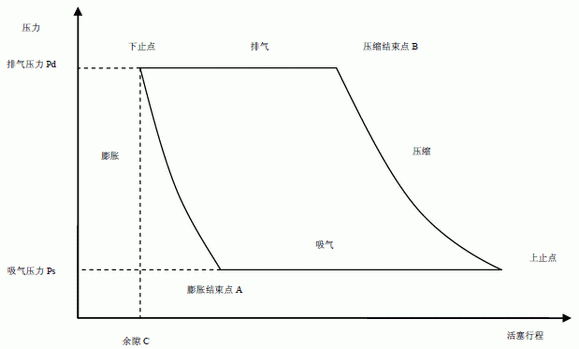
图 3 紧缩机整个行程中的P-V 联系
4.4.4 活塞顶部压力在运动剖析中的表现:
4.4.4.1 MSC.ADAMS 中IF 函数的界说
IF(expr1:expr2,expr3,expr4)
式中,expr1 为控制变量,expr2,expr3 和expr4 均为表达式。
函数F=IF(expr1:expr2,expr3,expr4)的意义为:
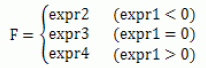
4.4.4.2 在本课题中IF 句子算法
图4 所示为本课题中紧缩机活塞端面受力IF 句子算法。先由活塞的速度方向(大于零/小于零),判别活塞运动处于吸气/胀大状况,仍是紧缩/排气状况,再依据活塞质心方位与胀大完毕点的联系确认是吸气状况仍是胀大状况;依据活塞质心方位与紧缩完毕点联系确认是紧缩状况仍是排气状况。
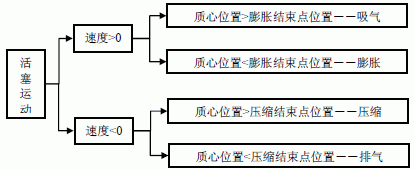
图4 活塞端面受力IF 句子算法
程序框图如图5 所示:
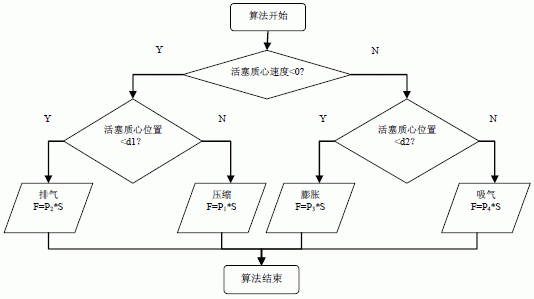
图5 活塞端面受力IF 句子程序框图
4.4.4.3 If 句子公式
将在UG 中建好的模型导入ADAMS 后,依据实践状况施加所需的运动束缚。设定End Time = 10,step = 100,进行开始动态运转,丈量所得数据。依据上述数据经过核算,得出在三种不同工况下,活塞的排气点d1,吸气点d2 的方位,如表5 所示。
表5 紧缩机活塞行程参数(2)
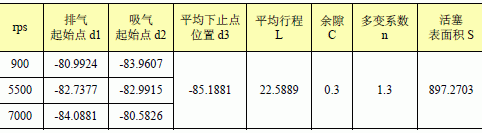
以活塞3 在工况900rps 下端面受力为例:吸气压力Ps=0.358MPa, 排气压力Pd=2.97MPa, 排气起始点方位d1=-80.9924, 吸气起始点方位d2=-83.9607,活塞均匀下止点方位d3=-85.1881, 活塞外表积S=897.2703, 活塞均匀行程L=22.5889,余隙C=0.3,多变系数n=1.3。
900r/min:
Piston_3 气体方程:
IF( VZ(piston3.cm):
IF(.5H11G.cm_dis3+80.9924:897.2703*2.97,897.2703*2.97,897.2703*0.358*((22.5889+0.3)/( .5H11G.cm_dis3+85.1881+0.3))**1.3),
IF(.5H11G.cm_dis3+80.9924:897.2703* 0.358, 897.2703*2.97, 897.2703 *2.97),
IF(.5H11G.cm_dis3+83.9607:897.2703*2.97*(0.3/(.5H11G.cm_dis3+85.1881+0.3))**1.3, 897.2703*0.358, 897.2703*0.358)
)
在模型上施加运动学束缚以及力束缚后,进行900rps 的运动仿真,以活塞3 为例,摘取其位移、速度、加速度与受力的曲线图,依据从前算出的d1、d2 方位,断定活塞在整个行程中的四个阶段的状况。一个周期内紧缩机进行胀大——吸气——紧缩——排气为一次完好循环。状况断定成果如图6 所示。
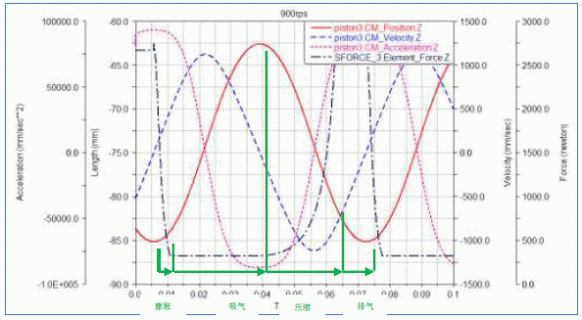
图6 位移、速度、加速度与受力的曲线图
5 剖析成果
5.1 运动学剖析
在转速为900rpm、吸气压强为0.358Mpa、排气压强为2.97Mpa 的工况下,如图7 和图8 所示,由于正五边形的对称性,一切活塞的位移幅值和端面受力曲线根本共同,相位差为2π /5。
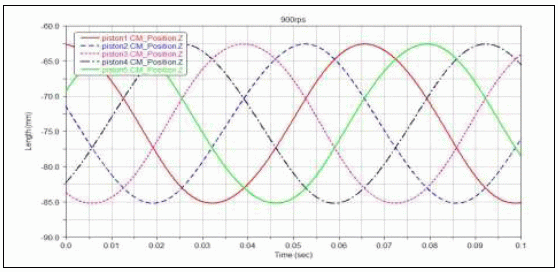
图7 活塞位移曲线(900rpm)
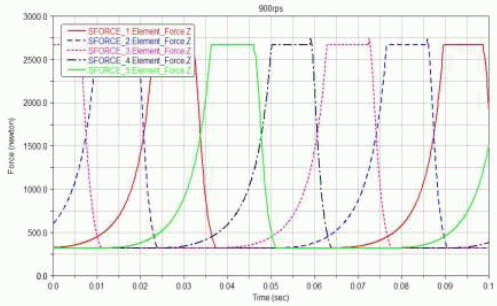
图8 活塞压力曲线(900rpm)
在活塞端面受力曲线中能够很显着的看到两段压力稳定的直线,对应了紧缩机作业中的吸气和排气状况(上端为吸气,下端为排气),两段曲线则别离对应了胀大和紧缩状况(左端为紧缩,右端为胀大),和上文使用速度方向和活塞质心方位断定成果共同。
由于导向杆的束缚所带来的对称性,使得挨近导向杆轴线的活塞(1 和5),其速度幅值要略大于远离轴线的活塞(2 和4)速度幅值,如图9 所示。导向杆所带来的对称性在加速度曲线图中尤为显着,如图10 所示,且处于对称轴线上的活塞3 的加速度曲线改变平稳而润滑,远离轴线的活塞(1 和5)的加速度曲线则呈现了必定的畸变,加速度的峰值相对原相位呈现了超前或滞后的现象。
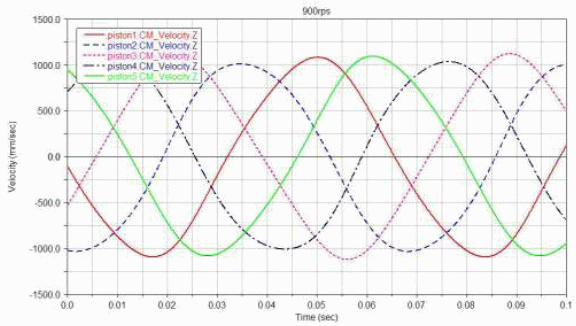
图9 活塞速度曲线(900rpm)
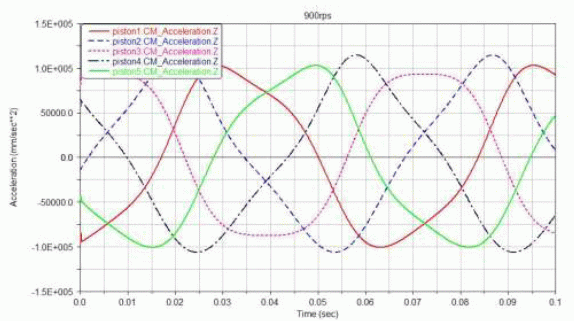
图10 活塞加速度曲线(900rpm)
呈现这种状况在很大程度上是由于导向杆的运动束缚形成的“轴对称性”而非抱负状况下的空间对称性,五个活塞在组织上并不处于彻底对等的方位所造成的。在满意了五个活塞在周向位移的要求的一起,由于连杆与行星盘的球铰链球心有不同程度的空间运动,使得速度和加速度的传递呈现了不同的成果。
5.2 动力学剖析
经过剖析可得导向杆头部的受力状况(图11)和紧缩机的功耗(图12)。经过导向杆的受力曲线咱们可将其作为有限元剖析的边界条件,剖析其应力,应变,和疲惫。
经过将模仿所得的功耗同实践状况的功耗进行比较,按规范在该工况下功耗应为2.75KW,同模仿所得的曲线均匀在2.7KW 是适当挨近的,然后也可证明剖析的精度是十分高的。
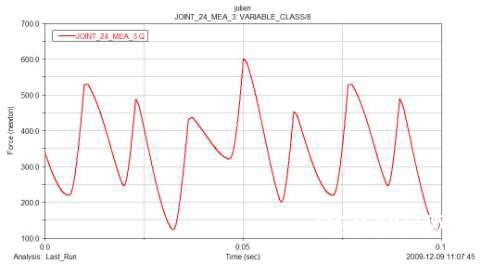
图11 导向杆头部受力曲线
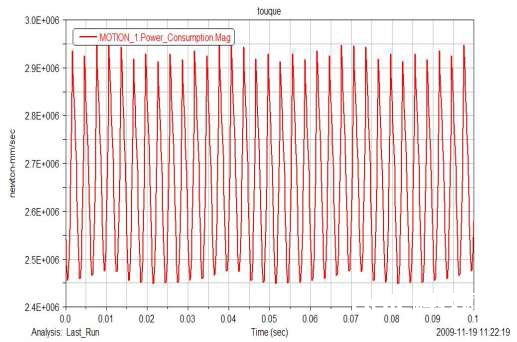
图12 紧缩机功耗曲线
6. 结语
经过剖析,咱们发现理论公式推导,和实验数据同软件运动学动力学仿真所得数据能达到较好的共同性。这说明前期三维实体建模和实体模型上的力学模型建立的正确性,并进一步验证了软件动力学仿真的可行性。这不只节省了很多的人力物力资源,更重要的是缩短了产品规划周期以减短了产品的出产制作周期,进步了优化规划的快捷性,降低了本钱。









