文氏桥电路是一个十分经典的电路,历经多年,虽然存在一些缺陷,但仍然是教科书里边的必讲内容。从电路结构来看,并不杂乱,可是这儿边隐含的常识点却许多,触及的内容也比较广泛,有信号与体系的常识,还要用到一点复变函数的常识,还触及到相位的概念。因而,值得把这个电路细心研究一下。
常识衬托
▶什么是文氏桥振动?
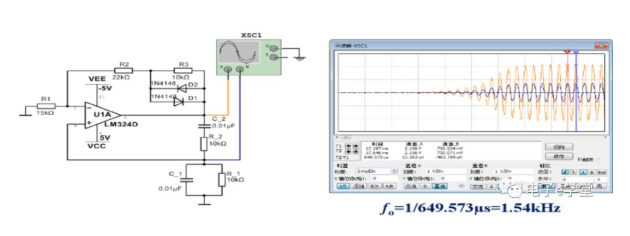
图1
如图1所示,左面是文氏桥的电路衔接方式,右边是仿真的成果,从示波器显现的成果,发现一个1.54KHz的正弦信号从无到有,就这么奇特的产生了,并且信号增大到必定幅值主动稳定下来。
咱们都知道,能量是守恒的,不可能随意产生一个信号,而这个电路没有任何输入的信号源,那这个正弦信号的能量来自哪里呢?答案是运放的供电电源。那这个电路之所以会产生这个信号,是由于自激振动的成果。
▶怎样才干让运放电路产生自激振动呢?
一个闭环的反应体系能够依照下面的结构图来描绘,如图2所示。
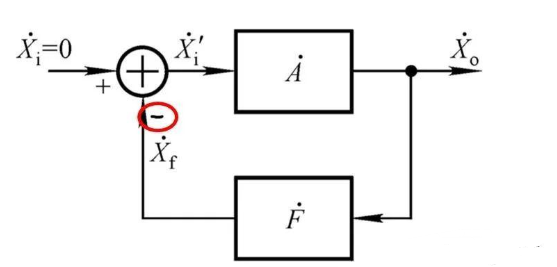
图2
A能够理解为正向通路体系函数,F为反应通路体系函数,Xi为输入量。依照图2中所画,实践上引进的是负反应,所以Xi’=Xi-Xf,Xo=AFXo。
咱们知道,沟通信号需求用幅值和相位才干描绘全面,那要想完成一个信号的自激, 需求一起满意幅值和相位条件:
幅值条件。 |AF|略》1,由于即使是1.00001,无数个1.00001相乘终究也会是无穷大。
相位条件。 一个信号从原点动身通过体系(A、F)走一圈,再回到原点时,要坚持和本来的信号相位共同,正弦信号的周期是360°;关于一个负反应体系而言,由于负反应本身就有180°的相位移动,所以需求附加±180°相移,才干使得信号与源信号同相。
而关于正反应体系,只需不引进额定的相移,就能够坚持和原信号同相。
还有一个隐含条件是Xi如果是0,那0扩大多少倍都是0,无法自激。因而,体系中咱们需求在一开始给入一个初始信号,不管这个信号有多小,终究会扩大出一个幅值客观的信号。
进入正题
咱们先看这个文氏桥振动电路的下半部分(图3),从输出端反应回来的信号接在的运放的同相端,实践上引进的是正反应,也便是说只需坚持在反应回路中不引进额定的相移就能够了。
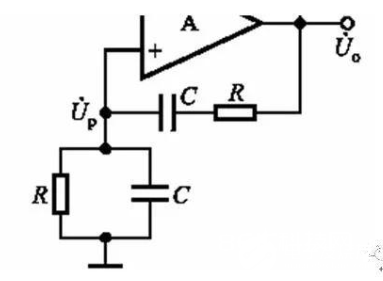
图3
可是在这个反应回路傍边,有电容的存在。咱们都知道,电容实践上会奉献复数里边的虚部,一旦引进电容,不可避免的要引进相移,那这个正反应的电路在这儿是起到什么效果呢?
先把电路提取出来,收拾一下,看的更清楚,如4所示。
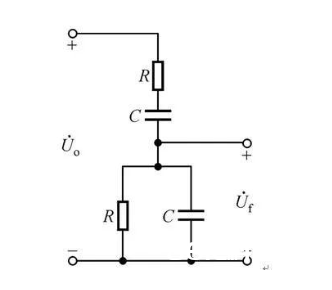
图4
对这个电路仿真一下,得到下面的幅频特性曲线(图5)。不难看出这是一个带通滤波电路,再由于2个R和2个C的取值共同,所以这是一个单频点的选频器,中心频率是1/(2πRC)。而带通滤波必定是由高通滤波和低通滤波组成,低通滤波使得信号的相位产生滞后,高通滤波使得信号相位超前;且由于R、C相同,高通与低通的特征频率共同,使得这个信号的相位移了2次又回到原点了,所以这儿完全是虚惊一场。
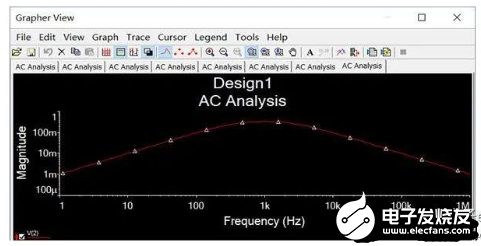
图5
关于这个正反应电路咱们还得深化分析,那最最底子的便是传递函数了,这儿有咱们想要的全部信息:
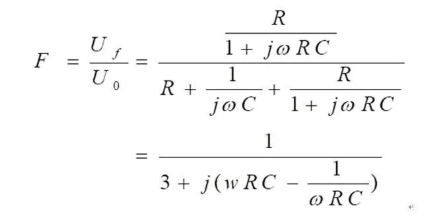
上面这个等式ω为角频率,这个式子要想取得最大值,需求让分母的模值最小,也便是分母的虚部为0。
令ωRC-1/(wRC)=0,求得ω=1/RC;再依据ω=2πf,推出f=1/(2πRC)时,整个正反应电路的模值|F|最大为1/3。
这儿其实也解说了为什么终究输出的信号频率是1.54kHz的问题,是依据1/(2πRC)算出来的,也只要这个频率的信号通过反应电路时幅值最大,并且没有相位移动,那你要想改动输出信号的频率,就去改R和C的值就好了。
上面咱们一向再说的是体系中的F,下面来说A,来看上半部分电路(图6):
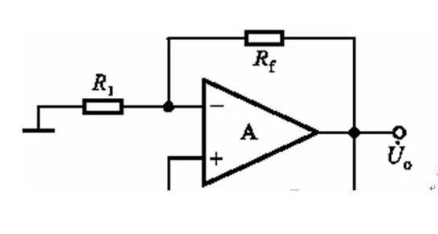
图6
这个电路咱们几乎再了解不过了,这便是一个典型的同相扩大器,扩大倍数为:A=(1+Rf/R1)。
这儿Rf与R1是不是随意取的呢?答案是否定的。由于上文现已知道|F|=1/3;要确保|AF|》=1,|A|有必要》=3;依据A=(1+RF/R1),推出(Rf/R1)》=2。
在一开始起振的时分,咱们需求让它Rf略》2R1,当信号到达必定起伏的时分,咱们不想让它持续添加,需求让Rf=2R1,由于这个时分|AF|=1,无数个1相乘,终究也是1,所以就稳定下来了。
那问题又来了,怎样能让这个Rf主动产生变化,然后使得输出稳定下来呢?
答案是参加稳幅电路,能够在Rf回路上参加2个二极管,也能够用一个负温度系数的热敏电阻,随电流添加,温度升高,能够主动下降本身阻值。
最终一个问题,便是巧妇难为无米之炊,一开始咱们需求把一个小信号给进去,这个小信号还要包括各种频率成分,才干在很多信号傍边挑选出咱们想要的进行自激扩大;而在实践电路中,其实很简单取得,由于在咱们的环境中,有各种频率的噪声,取之不尽用之不竭,所以这个就不必管了,它自己会进去的。
总 结
所以,一个体系要想完成自激振动需求满意2个条件: