导言
跟着多媒体技能的开展,呈现了各式各样的停止图画紧缩技能,其中最成功的当推JPEG规范。但由于有损紧缩的原因,传统JPEG在许多对图画质量要求较高的运用场合无法担任。与传统JPEG依据离散余弦改换不同,JPEG2000依据离散小波改换,它不仅在紧缩功用方面显着优于JPEG,还具有许多JPEG无法供给或无法有用供给的新功用,比方,一起支撑有损和无损紧缩、大幅图画的紧缩、渐进传输、感兴趣区编码、杰出的鲁棒性、码流随机拜访等。一个典型的JPEG2000的紧缩进程如图1所示。

图1 JPEG2000的紧缩进程
由图1所示,预处理一般包括三种操作:区域区分,下降量级,重量改换。预处理后的数据将进行离散小波改换(DWT),以进一步下降数据之间的相关性。JPEG2000的量化与JPEG量化根本相同,总体上都是选用均匀量化,不同子带的量化步长一般不同。量化今后,榜首层编码(自适应算术编码)选用EZW的改善算法SPIHT算法将等候编码的、经过小波改换后的比特流按重要性不同进行排序,供给多个满意不同方针码率或失真度的切断点,使得解码器方能依据方针码率或失真度的要求在某一切断点完毕解码,供给相应质量的图画。第二层编码(码流安排)将上述切断的数据进行打包,并附加相关的标志信息,然后完成JPEG2000对多失真度的支撑。
离散小波改换体系
小波剖析进行图画紧缩根本原理是:依据二维小波分化算法,一幅图画做小波分化后,可得到一系列不同分辨率的图画,而体现一幅图画最首要的部分是低频部分,假如去掉图画的高频部分而只保存低频部分,则可到达图画紧缩的意图。传统傅立叶剖析只能对信号进行时域或频域独自进行剖析,时域上有限的信号在频域是无量的,频域内有限的信号在时域里是无量的。而小波剖析能在时域和频域内一起剖析,且能主动调整分辨率。
与其他运用小波改换的其他图画紧缩规范比较,JPEG2000在小波改换的基础上选用更为杂乱精密的小波块切割算法,即优化截取的嵌入式块编码EBCOT算法,然后完成了丰厚的功用,比方依据感兴趣区域编码ROI,即对一幅图画中感兴趣的部分选用低紧缩比以获取较好的图画作用,而对其他部分选用高紧缩比以节约存储空间,这样就能够经过点击ROI部分以取得更高的分辨率,看到图画的细节部分。
在本体系中,选用第二代小波改换的快速提高算法CDF9/7双正交小波改换,小波改交换CDF9/7双正交小波基,该小波基具有线性相位,因此有着极好的图画紧缩功用。其完成进程如图2所示。
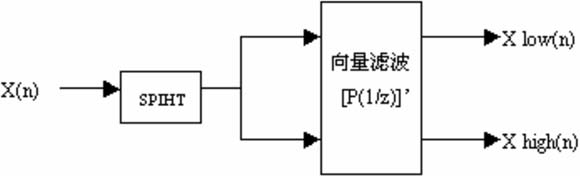
图2 CDF9/7双正交小波改换的完成进程
图3是用CDF9/7小波族对一个的图画做两级DWT剖析的状况。在第二级中,榜首级得到的低通近似自身被分红4个子图画,提取出了细节,留下一个新的低通近似。低通滤波的作用很简单从围巾、桌布的斑纹,藤椅的方格,远处罗列的书本这些细节的丢掉看出。第二级低通近似也能够持续改换,以生成4幅新的子图画。这种改换能够一向进行下去知道子图画只包括一个像素停止。
a 原始图画
b二维DWT剖析图画

图3 两级二维DWT剖析
在图3中,笔直细节对应于剖析块的右上角,水平细节对应于左下角,而对角细节对应于右下角,它们都体现出了较强的外观。当数字图画需求经过二维DWT子图画重建时,就要用向上采样和卷积的方法将细节与低通近似组合起来。
SPIHT图画编码
为了验证JPEG2000体系的可行性及功用,选用MATLAB对体系中的小波改换部分进行了仿真,然后用C++语言对小波改换后的系数进行编解码,完成体系中第二部分的仿真,以大幅下降数据量。SPIHT是依据内嵌零树编码(EZW)的集切割算法,C++中的链表类能完成SPIHT算法中的三个操控链表(LSP,LIP和LIS),便利的位操作指令合适处理算法中依据位平面的编解码功用。
为了对小波改换和SPIHT编码算法有更直观的知道,下面从一幅图画中选取尺度的像素矩阵进行处理,剖析每一步处理后数据的改变。
初始图画矩阵如图4所示,所用图画是256色(每像素8位),像素灰度图。
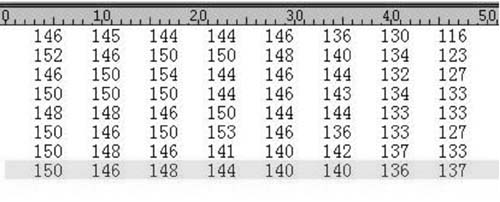
图4 图画xiaoshutiao.bmp中的一部分数据
由上图能够看出图画幅值散布比较随机,没有什么规则。对上数据进行离散小波改变后的数据如图5所示,小波改换选用依据提高的CDF9/7双正交小波基,进行5级分化。
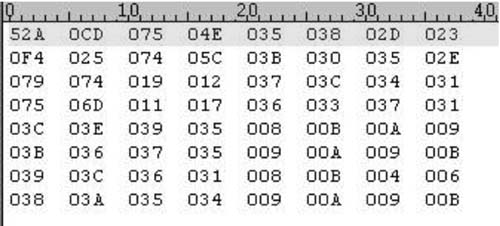
图5 三级小波改换后的系数数据
由上图数据能够看出,幅值大的数据首要散布于左上交,这与小波改换后的数据散布特点是共同的,即榜首级是低频图画概貌数据,集中了图画大部分的能量,其他各级是分辩率不同的图画的高频细节数据,反映图画水平、笔直、和歪斜方向的纹路信息,故大数据呈线状散布,总能量比较少,便于对数据进行不同分辩质量的紧缩。
对上数据进行SPIHT编码后的数据见图6所示。
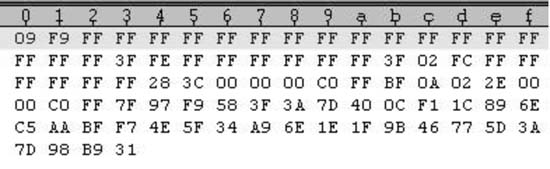
图6 SPIHT编码数据
从上图数据能够看出,连1数据和连0数据都较多,可对其作进一步的游程编码。游程编码即记载数据中连0和连1的个数数据的紧缩方法。编码后的数据见图7。
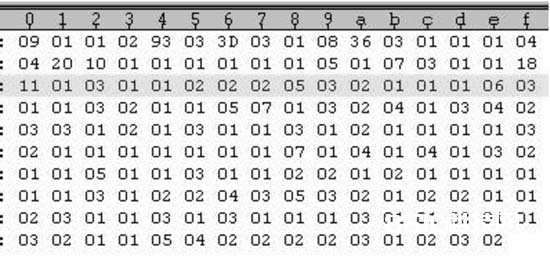
图7 游程编码数据
在对上数据作进一步的哈夫曼编码,哈夫曼编码是一种无损最优编码方案,如图8所示。

图8 Huffman编码数据
留意上述整个编码都是无失真的,也即经过一系列的解码进程能够彻底恢复出原始图画。假如对原始图画进行某一等级分辨率的紧缩后可大大下降数据量。
结语
本文介绍了小波改换在图画紧缩JPEG2000里的运用。小波改换不同于传统的域改换紧缩方法,它对图画全体进行改换,取得一系列不同分辨率的图画概貌信息和细节信息,然后为进一步处理供给很大的地步。一起经过对一种依据嵌入式零树思维的集切割SPIHT算法的仿真,阐明该算法功用高、核算量小,若在JPEG2000体系中编解码选用同一套算法,能够大大下降了解码算法的杂乱性,是一种很有出路的图画编解码技能。