在多路实时语音处理体系中,依据高斯混合概率模型[1,2]的体系后端运算量非常大,选用log-add算法单元可以简化运算,进步运算功率。其函数方法为[3]:

查表法可以认为是多项式次数为0的状况,跟着精度要求的添加,查找表会变得很大[5]。函数迫临可以选用多项式拟合,首要依据所需求的精度确认多项式次数和分段的巨细,然后核算每一段的多项式系数。
设分段的巨细为d(d=2-k,k=0,1,2…),核算各段系数时,各段函数平移到区间[0,d),如图2所示。用Matlab进行多项式拟合顺次得到各段系数。由此可以得出各段的拟合多项式为:

这样完成时可以把二进制的定点数x分为MSBs和LSBs两段。MSBs对应段标号i,由段标号取出系数ci0,ci1,ci2…;LSBs对应浮点数xl,代表段内偏移值。由图3可以核算出f(x)。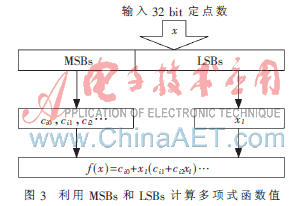
MSBs和LSBs应该这样选取,例如定标为Q32.f,挑选d=1/2,则MSBs为高32-(f-1)位,LSBs为低f-1位;挑选d=1/4, 则MSBs为高32-(f-2)位,LSBs为低f-2位……;假如MSBs为32或31,则变成了查表法。
2 多项式拟合的完成计划
2.1 多项式次数与分段巨细、精度的联系
用Matlab进行仿真,表1列出了各种精度要求下各次多项式所需的分段巨细(d),其间?啄为精度要求,?茁为多项式的次数。
由表1可以看出,相同次数的状况下,精度要求越高,分段巨细d越小;而相同精度的状况下,次数越高,分段巨细d越大。别的,次数越低,精度越高,分段巨细d下降的数量级越快。

表2列出各次多项式在不同精度要求下,所需求系数个数(n)的散布状况。
由表2可以看出,其成果与表1趋于共同。相同次数下,精度要求越高,所需求的系数个数n越多;而相同精度下,次数越高,所需求系数个数n越少。n跟着次数的下降和精度的进步敏捷增大。
与n相反,多项式的核算量跟着多项式次数的添加而添加。依据horner算法[3]多项式的表达式如下:
式(6)标明,多项式次数添加1次,核算多项式的函数值添加1次乘法和1次加法。多项式系数存储量与多项式的核算量是其FPGA完成时互相制约的两个要素。
3 仿真成果
为了获得面积与速度的平衡,依据测验成果及实践体系的要求,挑选δ=10-4、β=1来完成。本文选用Xilinx ISE Design Suite 10.1进行仿真测验。定标取Q32.23,其硬件完成核算流程如图4,输入为定点数x,由MSBs和LBSs获得系数和xl,通过reg系数寄存器及1次乘法和1次加法,输出y。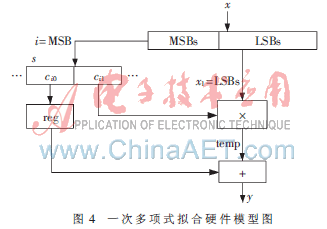
时序仿真成果成果如图5。输入x是32 bit的无符号定点数,输出为y;clk是时钟;reset为复位信号;MSBs是x的高位,用于得到多项式系数;LSBs是x的低位即自变量;temp是用于缓存中心成果,coef[…]是多项式系数。输出推迟3个时钟周期,流水线填满后,每个时钟周期输出一个成果。
例如输入32’h00333333(浮点数0.4),从图中可以看出其输出y为24’h41aba5,与实践函数值24’h41aa7c存在差错。其完成成果与浮点成果比较差错如图6。可以看出定点数差错在800以内,也便是浮点数约10-4以内,差错规模与表1相共同。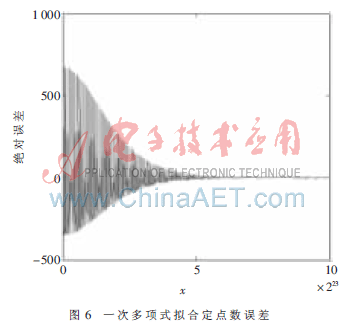
运用ISE软件的XST东西归纳,挑选设备为Xilinx公司Virtex5系列的XC5VFX100T(speed-2)。其资源占用状况如表3,其间Xilinx公司的乘加硬件设备DSP48E用于算法中的乘法运算及加法运算[6]。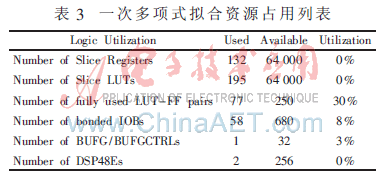
可以比照δ=10-4,β=0,1,2,3四种完成方法的硬件开支,如表4。
由表4可以看出,尽管多项式次数为0时运用寄存器(Registers)和查找表(LUTs)最少,且乘法和加法次数(DSP48Es)为0,但由于其运用了24×40 960 ROM,占用存储面积较大;而一次多项式拟合尽管所占用查找表(LUTs)一项相对较多,但归纳考虑,其他资源占用都比较均衡。其全体的资源开支要好于其他计划。
log-add算法单元作为高斯混合概率模型FPGA完成的根本算法单元,可以简化运算、进步运算功率。在体系精度要求10-4的状况下,选用一次多项式拟合可以有效地节约硬件开支,完成简略快速log-add算法单元,为大规模实时处理多路语音数据供给了重要确保。









