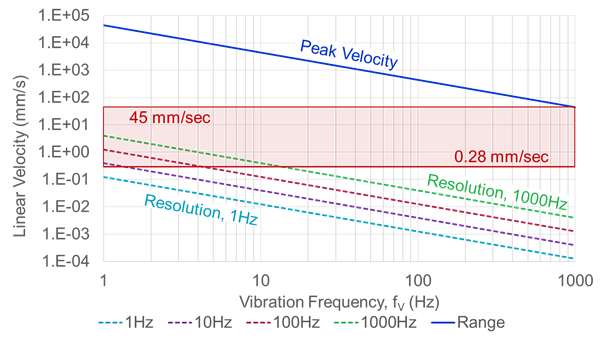
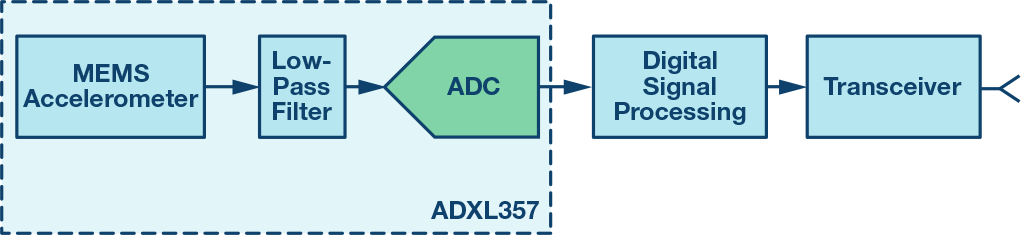
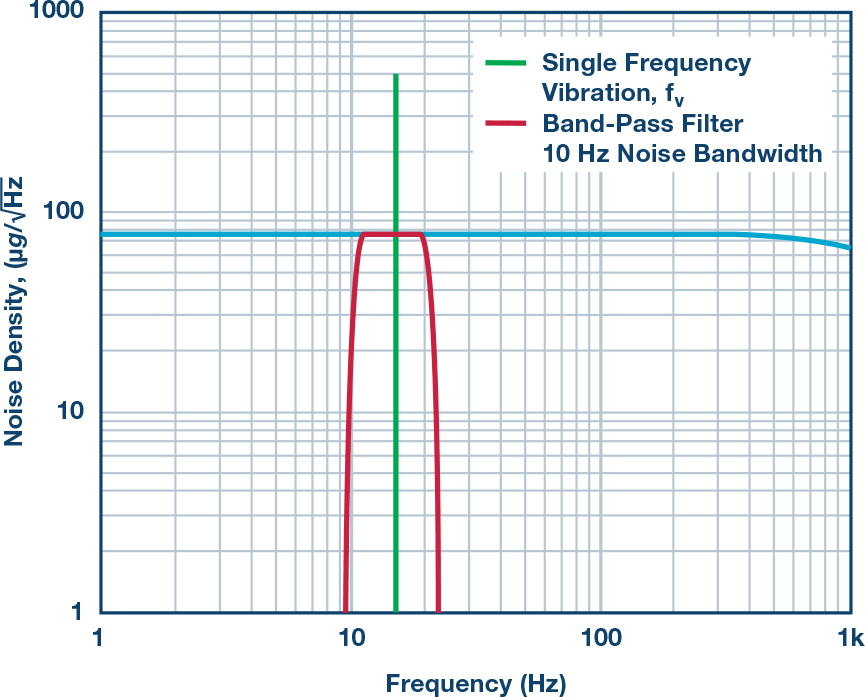
文章转自ADI官网,版权归属原作者一切 MEMS加速度计总算达到了可以丈量广泛机器渠道振荡的阶段。其最近的才干前进,加上MEMS加速度计已有的相关于传统振荡传感器的许多优势(尺度、分量、本钱、抗冲击性、易用性),促进一类新式的状况监控(CBM)体系开端运用MEMS加速度计。成果,许多CBM体系架构师、开发者乃至其客户初次考虑运用此类传感器。他们面对的问题常常是怎么快速了解评价MEMS加速度计功用的办法,以便在其机器渠道上丈量最重要的振荡特性。这初看起来好像很困难,由于MEMS加速度计数据手册表述最重要功能特性的办法常常不是开发人员所了解的。例如,许多人了解用线速度(mm/s)来量化振荡,但大大都MEMS加速度计数据手册是用依据重力的加速度(g)来表达其功能目标。走运的是,有一些简略的技能可用来将加速度转化为速度,以及估量加速度计要害特性(频率呼应、丈量规模、噪声密度)对重要体系级规范(带宽、平整度、峰值振荡、分辩率)的影响。 先从惯性运动视点调查线性振荡。在此布景下,振荡是均匀位移为零的机械振荡。关于那些不期望其机器穿越整个车间的人来说,零均匀位移非常重要!振荡检测节点中中心传感器的价值与它反映机器振荡最重要特性的才干凹凸直接相关。要评价特定MEMS加速度计在这方面的才干,首要有必要从惯性运动视点对振荡有一个根本了解。图1是振荡状况的物理示意图,灰色部分表明中点,蓝色部分表明一个方向的峰值位移,赤色部分表明另一方向的峰值位移。等式1供给了一个描绘矩形物体瞬时加速度的数学模型,其振荡频率为(fV),起伏为Arms。 在大部分CBM运用中,机器渠道的振荡常常有比等式1所示模型更杂乱的频谱特征,但此模型为学习发现之旅供给了一个很好的起点,由于它给出了CBM体系常常会盯梢的两个常见振荡特性:起伏和频率。此办法对要害特性到线性速度项的转化也很有用(稍后将有更多阐明)。图2供给了两类不同振荡模式的频谱视图。第一类(拜见图2中的蓝线)在其频率规模(f1到f6)内具有稳定起伏。第二类(拜见图2中的红线)在四个不同频率处呈现了峰值起伏:f2, f3, f4, 和 f5. 丈量规模、频率规模(带宽)和分辩率是用来量化振荡检测节点才干的三个常见特性。图2经过虚线矩形框显现了这些特性,其鸿沟别离对应最低频率(fMIN)、最高频率(fMAX)、最小起伏(AMIN)和最大起伏(AMAX)。当考虑将MEMS加速度计用作振荡检测节点中的中心传感器时,体系架构师很或许想在规划前期剖析其频率呼应、丈量规模和噪声行为。有一些简略的技能可用来评价加速度计的各种特性,从而预判其是否满意指定的一组要求。很显然,体系架构师终究有必要经过实践验证和判定来核验上述估量,但由对加速度计才干的前期剖析和猜测所得来的期望对这些作业是有价值的。 图2供给了一个简略的一阶模型,其描绘了时域中MEMS加速度计对线性加速度(a)的呼应(y)。在该联系中,偏置(b)表明传感器无振荡时的输出值。份额因子(KA)表明MEMS加速度计呼应(y)相关于线性加速度(a)改变的改变量。 传感器的频率呼应描绘份额因子(KA)相关于频率的值。在MEMS加速度计中,频率呼应主要有两个奉献要素:(1) 其机械结构的呼应;(2) 其信号链中的滤波呼应。等式3供给了一个通用二阶模型,其近似描绘了MEMS加速度计机械部分对频率的呼应。在该模型中,fO表明谐振频率,Q表明品质因数。 信号链的奉献常常取决于运用所需的滤波。某些MEMS加速度计运用单极点低通滤波器来协助下降谐振频率时的呼应增益。等式4为此类滤波器相关的频率呼应(HSC)供给了一个通用模型。在该类滤波器模型中,截止频率(fC)表明输出信号起伏比输入信号低√2倍时的频率。 等式5将机械结构(HM)和信号链(HSC)的奉献进行了兼并。 图3直接运用此模型来猜测ADXL356(x轴)的频率呼应。此模型假定标称谐振频率为5500 Hz,Q为17,运用截止频为1500 Hz的单极点低通滤波器。留意,等式5和等式4仅描绘了传感器的呼应。此模型未考虑加速度计与其监控的渠道的耦合办法。 在运用单极点低通滤波器(例如等式4所用)树立频率呼应的信号链中,其带宽规范常常阐明晰其输出信号供给输入信号50%功率时的频率。关于更杂乱的呼应,例如等式5和等式3中的三阶模型,带宽规范常常带有相应的平整度规范。平整度特性描绘比率因子在频率规模(带宽)内的改变。运用图3和图5中的ADXL356仿真,1000 Hz时的平整度约为17%,2000 Hz时的平整度约为40%。 尽管许多运用由于平整度(精度)要求而需求约束可以运用的带宽,但对有些运用来说,这或许不是问题。例如,某些运用或许更重视盯梢随时刻的相对改变,而不是肯定精度。另一个比如是运用数字后处理技能来消除用户最关怀的频率规模上的纹波。关于此类状况,在给定频率规模时,呼应的可重复性和稳定性常常比呼应的平整度更重要。 MEMS加速度计的丈量规模目标表明传感器的输出信号可以盯梢的最大线性加速度。在超出额外丈量规模的线性加速度水平,传感器的输出信号会饱满。这种状况会引起严峻失真,导致难以(乃至无法)从丈量成果提取有用信息。因而,有必要保证MEMS加速度计可以支撑峰值加速度水平(拜见图2中的AMAX)。 留意,丈量规模与频率有必定的联系,由于传感器的机械呼应会引进某种呼应增益,增益呼应的峰值呈现在谐振频率时。关于ADXL356的仿真呼应(拜见图3),增益峰值约为4倍,故丈量规模从±40 g降至±10 g。等式6供给了一种剖析办法来猜测此值,它以等式5为起点: 份额因子的大幅改变和丈量规模的下降,是大大都CBM体系期望将其遭受的最大振荡频率约束在远低于传感器谐振频率水平的两个原因。 仪器分辩率可界说为环境中引起仪器示数发作可检测改变的最小值。”1在振荡检测节点中,加速度丈量的噪声会直接影响其检测振荡改变的才干(即”分辩率”)。因而,关于那些正在考虑运用MEMS加速度计检测其机器渠道上细小振荡改变的人来说,噪声行为是一个重要考虑要素。等式7供给了一个用于量化MEMS加速度计噪声对其分辩细小振荡改变才干的影响的简略联系式。在该模型中,传感器的输出信号(yM)等于其噪声(aN)与其饱尝的振荡(aV)之和。由于噪声(aN)与振荡(aV)没有相关性,所以传感器输出信号的起伏(|yM|)等于噪声起伏(|aN|)与振荡起伏(|aV|)的和方根(RSS)。 那么,需求何种振荡水平才干战胜丈量中的噪声担负,在传感器输出信号中发生可观测的呼应?依据噪声水平量化振荡水平有助于以剖析办法探求这个问题。等式8经过比率(KVN)确认了这一联系,然后依据该比率导出了一个猜测传感器输出改变水平的联系: 表1供给了此联系的一些数值比如,以协助阐明传感器输出丈量成果相关于振荡与噪声起伏之比(KVN)的添加。为简明起见,本文剩下部分假定传感器丈量的总噪声决议其分辩率。从表1可知,这对应于KVN为1的状况,即振荡起伏等于噪声起伏。在这种状况下,传感器的输出起伏相关于零振荡时的输出起伏会添加42%。留意,为了确认该状况下分辩率的相关界说,每种运用或许需求考虑体系中可观测到何种水平的添加。 图4显现了一个选用MEMS加速度计的振荡检测节点的简化信号链。大大都状况下,低通滤波器会供给某种抗混叠支撑,而数字处理睬供给更清晰的频率呼应鸿沟。一般来说,这些数字滤波器会尽力维护代表实践振荡的信号内容,一同将带外噪声的影响降至最低。因而,当估量噪声带宽时,数字处理是体系中要考虑的影响最大的部分。此类处理可选用时域技能,例如带通滤波器,或选用频谱技能,例如快速傅里叶变换(FFT)。 等式9供给了一个用于估量MEMS加速度计丈量总噪声(ANOISE)的联系式,其间运用了噪声密度(φND)和与信号链相关的噪声带宽(fNBW)。 运用等式9中的联系,咱们可以估量:当对ADXL357(噪声密度为80 μg/√Hz)运用噪声带宽为100 Hz的滤波器时,总噪声将为0.8 mg (rms)。 某些CBM运用需求用线速度来衡量中心加速度特性(规模、带宽、噪声)。进行这种转化的一种办法是从图1所示简略模型开端,并运用相同的假定:线性运动、单一频率和零均匀位移。等式10经过图1中物体瞬时速度(vV)的数学联系式表述了该模型。此速度的起伏(表明为均方根rms)等于峰值速度除以√2。 等式11对此联系求导,得出图1中物体瞬时加速度的联系式: 从等式11中加速度模型的峰值动身,等式12导出了加速度起伏(Arms)与速度起伏(Vrms)和振荡频率(fv)的新联系式。 现在以ADXL357为例进行研讨,将上述内容汇总起来,用线速度表明其规模(峰值)和1 Hz至1000 Hz振荡频率规模内的分辩率。图5供给了对本事例有影响的多个特性的图形界说,从ADXL357噪声密度相关于1 Hz至1000 Hz频率规模的联系曲线开端。为了简化评论,本事例研讨中的一切核算均假定悉数频率规模内的噪声密度为稳定值(φND = 80 μg/√Hz)。图5中的赤色频谱曲线表明带通滤波器的频谱呼应,绿色竖直线表明单一频率(fV)振荡的频谱呼应,其对依据速度估量分辩率和规模会很有用。 此进程的第一步是运用等式9估量四个不同噪声带宽(fNBW)发生的噪声(ANOISE):1 Hz、10 Hz、100 Hz和1000 Hz。表2用两个不同单位的线速度给出了这些成果:g和mm/s2。g在大都MEMS加速度计规范表中适当常见,但振荡目标常常不是以此来供给。走运的是,g和mm/s2的联系已为我们熟知,拜见等式13。 本事例研讨的下一步是收拾等式12中的联系,以导出一个简略的公式(拜见等式14)来将总噪声估量(来自表2)转化为线速度项(VRES、VPEAK)。除了供给此联系的一般方式之外,等式14还供给了一个特定比如,其运用10 Hz的噪声带宽(及2.48 mm/s2的加速度噪声,来自表2)。图6中的四条虚线表明一切四种噪声带宽下相关于振荡频率(fv)的速度分辩率。 除了显现各带宽对应的分辩率之外,图6还有一条蓝色实线,其表明相关于频率的峰值振荡水平(线速度)。这来自等式15中的联系,其一般方式与等式14相同,但不运用分子中的噪声,而运用ADXL357支撑的最大加速度。留意,分子中的系数√2会扩大此最大加速度以反映均方根水平,假定选用单一频率振荡模型。 最终,红框阐明怎么将此信息运用于体系级要求。此红框中的最小(0.28 mm/s)和最大(45 mm/s)速度来自关于机器振荡的常用工业规范中的一些分类水平:ISO-10816-1。将关于ADXL357规模和分辩率曲线的要求放在一同便可快速得出一些简略的定论,例如: MEMS已是老练的振荡传感器,在现代工厂CBM体系的技能交融完美风暴中发挥着重要作用。检测、衔接、存储、剖析和安全范畴的新解决方案全都相互交融,为工厂管理者供给彻底集成的振荡观测和进程反应控制体系。尽管很简略迷失在一切此类惊人技能前进所带来的振奋之中,但人们仍需求了解怎么将传感器丈量成果与实践条件和其代表的意义联系起来。这些简略的技能和见地供给了一种将MEMS功能规范转化为运用了解的单位表明的其对要害体系级规范影响的办法,CBM开发商及其客户将能从中获取价值。简介
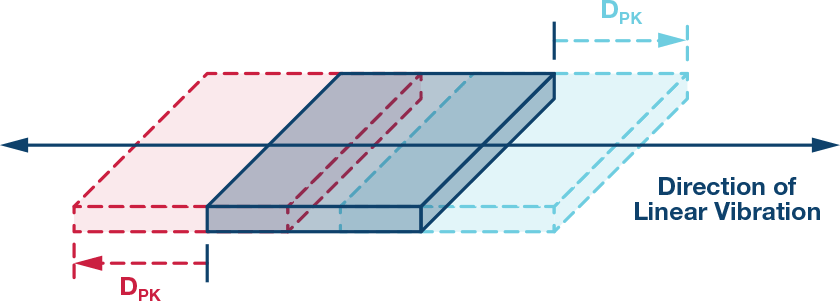
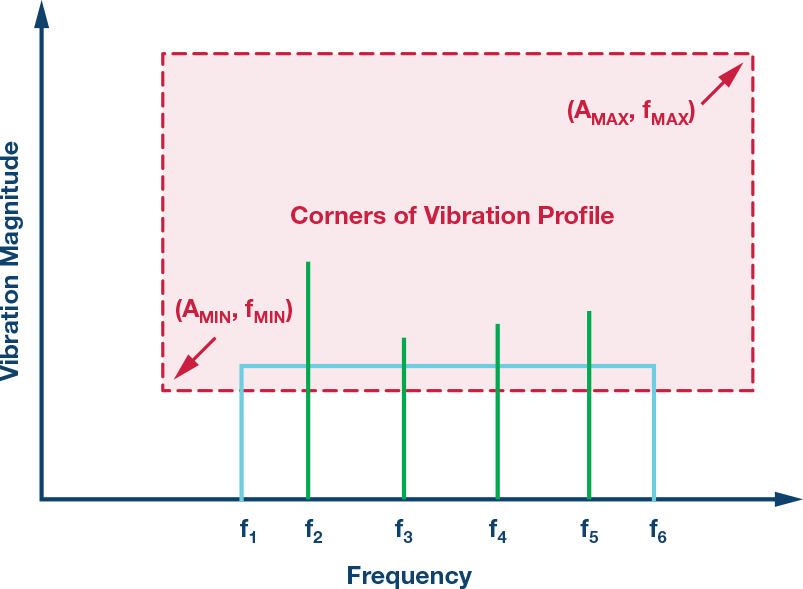
根本振荡特性
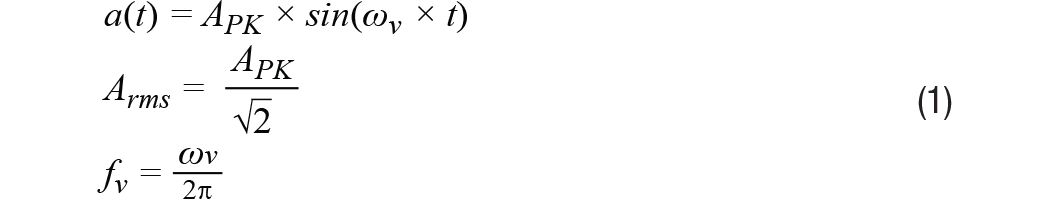
体系要求
频率呼应

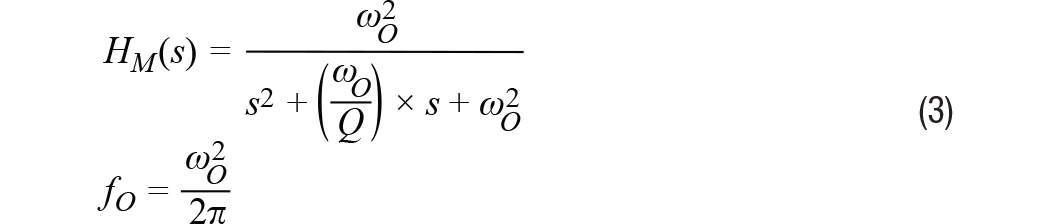

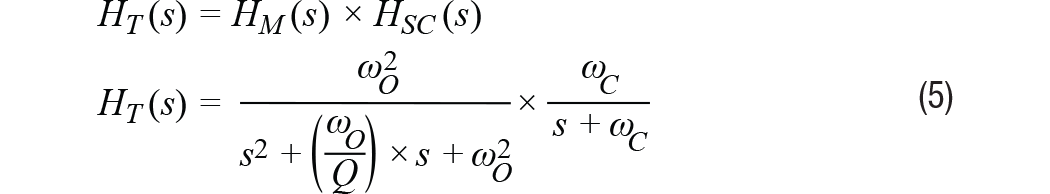
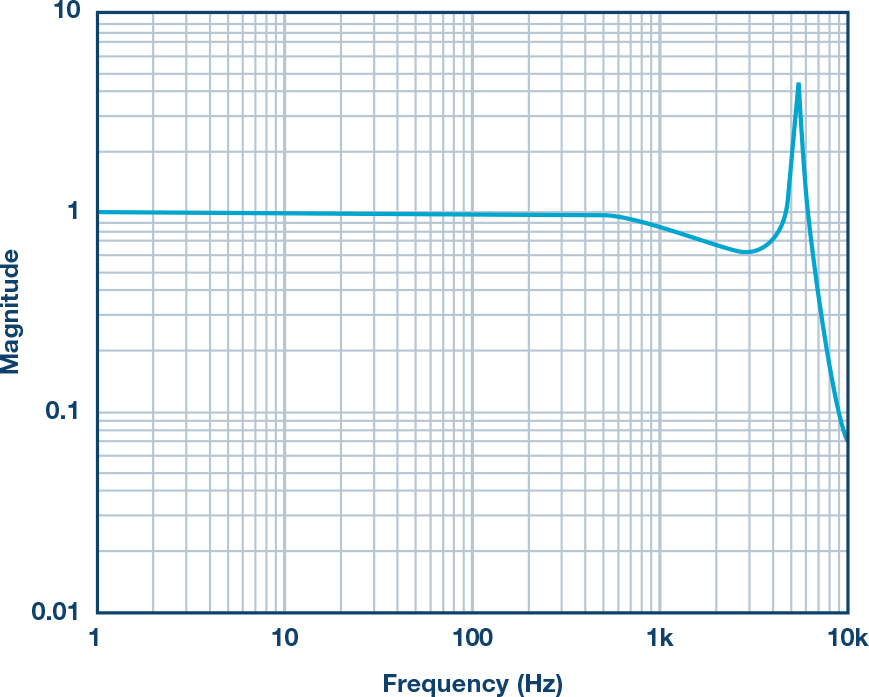
带宽与平整度的联系
丈量规模

分辩率

KVN
lyMl/laNl
添加%
0
1
0
0.25
1.03
3
0.5
1.12
12
1
1.41
41
2
2.23
123
猜测传感器噪声

用速度衡量振荡

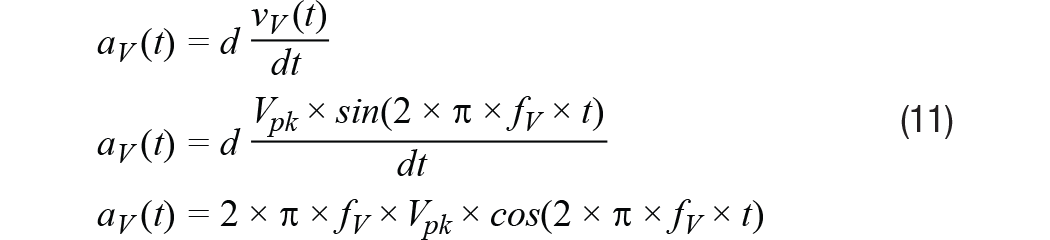

事例研讨

fNBW(Hz)
ANOISE
(mg)
(mm/s2)
1
0.08
0.78
10
0.25
2.48
100
0.80
7.84
1000
2.5
24.8
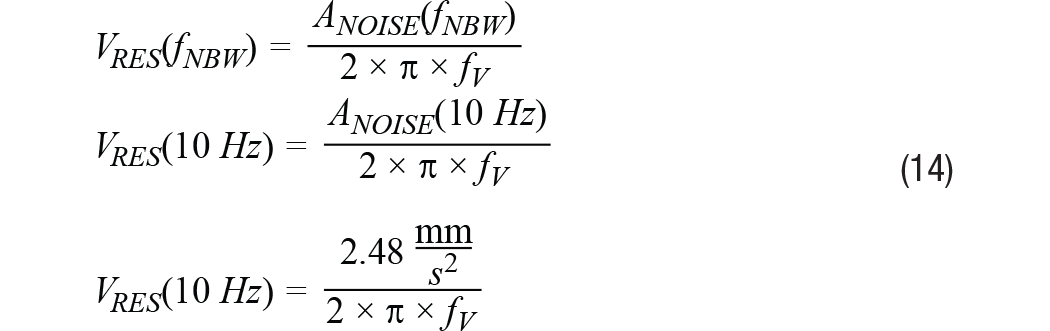

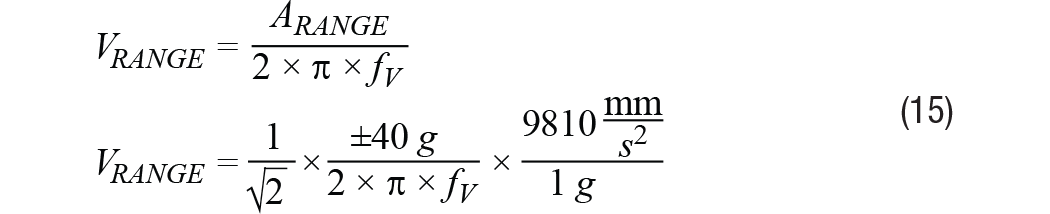
结语
参阅电路
1. Gerald C. Gill and Paul L. Hexter. “IEEE地球科学电子论文集.” IEEE,第11卷第2期,1973年4月。