大家好,又到了每日学习的时刻了,今日咱们来聊一聊数字信号处理中DFT、DTFT和DFS的联络,咱们通过几幅图来比照,评论一下哦。
许多同学学习了数字信号处理之后,被里面的几个名词搞的晕头转向,比方DFT,DTFT,DFS,FFT,FT,FS等,FT和FS归于信号与体系课程的内容,是对接连时刻信号的处理,这儿就不过多评论,只解说一下前四者的联络。
首要阐明一下,我不是数字信号处理专家,因而这儿只站在学习者的视点以最深入浅出的性质来解说问题,而不涉及到任何公式运算。
学过卷积,咱们都知道有时域卷积定理和频域卷积定理,在这儿只需要记住两点:1.在一个域的相乘等于另一个域的卷积;2.与脉冲函数的卷积,在每个脉冲的方位大将发生一个波形的镜像。(在任何一本信号与体系课本里,此两条性质有具体公式证明)
下面,就用这两条性质来阐明DFT,DTFT,DFS,FFT之间的联络:
先看图片:
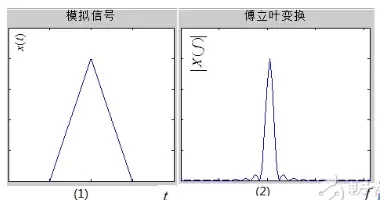

首要来说图(1)和图(2),关于一个模仿信号,如图(1)所示,要剖析它的频率成分,有必要改换到频域,这是通过傅立叶改换即FT(Fourier Transform)得到的,所以有了模仿信号的频谱,如图(2);留意1:时域和频域都是接连的!
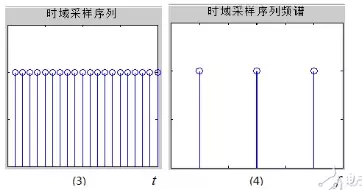
可是,核算机只能处理数字信号,首要需要将原模仿信号在时域离散化,即在时域对其进行采样,采样脉冲序列如图(3)所示,该采样序列的频谱如图(4),可见它的频谱也是一系列的脉冲。
所谓时域采样,便是在时域对信号进行相乘,(1)×(3)后能够得到离散时刻信号x[n],如图(5)所示;由前面的性质1,时域的相乘相当于频域的卷积,那么,图(2)与图(4)进行卷积,依据前面的性质2知,会在各个脉冲点处呈现镜像,所以得到图(6),它便是图(5)所示离散时刻信号x[n]的DTFT(Discrete time Fourier Transform),即离散时刻傅立叶改换,这儿着重的是“离散时刻”四个字。留意2:此刻时域是离散的,而频域仍然是接连的。
通过上面两个过程,咱们得到的信号仍然不能被核算机处理,由于频域既接连,又周期。咱们天然就想到,已然时域能够采样,为什么频域不能采样呢?这样不就时域与频域都离散化了吗?
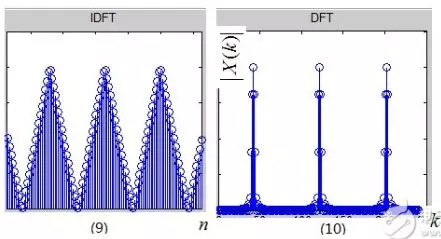
没错,接下来对频域在进行采样,频域采样信号的频谱如图(8)所示,它的时域波形如图(7)。现在咱们进行频域采样,即频域相乘,图(6)×图(8)得到图(10),那么依据性质1,这次是频域相乘,时域卷积了吧,图(5)和图(7)卷积得到图(9),果然如此的,镜像会呈周期性呈现在各个脉冲点处。
咱们取图(10)周期序列的主值区间,并记为X(k),它便是序列x[n]的DFT(Discrete Fourier Transform),即离散傅立叶改换。可见,DFT仅仅为了核算机处理便利,在频率域对DTFT进行的采样并截取主值罢了。
有人或许疑问,对图(10)进行IDFT,回到时域即图(9),它与原离散信号图(5)所示的x[n]不同呀,它是x[n]的周期性延拓!
没错,因而你去查找一个IDFT的界说式,是不是对n的取值区间进行约束了呢?这一约束的意义便是,取该周期延拓序列的主值区间,即可复原x[n]!
FFT呢?FFT的提出彻底是为了快速核算DFT罢了,它的实质便是DFT!咱们常用的信号处理软件MATLAB或许DSP软件包中,包括的算法都是FFT而非DFT。
DFS,是针对时域周期信号提出的,假如对图(9)所示周期延拓信号进行DFS,就会得到图(10),只需截取其主值区间,则与DFT是彻底的一一对应的准确联络。这点对照DFS和DFT的界说式也能够容易的看出。因而DFS与DFT的实质是相同的,只不过描绘的办法不同罢了。
不知道通过上面的解说,您是否理解各种T的联络了呢?假如您不是算法设计者,其实只需懂得怎么运用FFT剖析频谱即可,博主近期会更新一篇文章,专门介绍怎么使用FFT剖析简略信号的频谱。
其实个人认为,纠结了这么多,便是为了打破实际模仿国际与核算机数字国际的边界呀!
今日就聊到这儿,各位,加油。