在高速串行数据的测验中,颤动的测验十分重要。在串行数据的颤动测验中,颤动界说 为信号的边缘与其参阅时钟之间的误差。关于颤动丈量值的量化,一般有颤动的峰峰值和有效值这两个参数。不过,颤动的峰峰值跟着丈量时刻的添加,丈量值不断 变大,不能将颤动值与误码率直接联系起来,所以关于颤动测验,颤动的峰峰值并不是一个抱负的目标来很衡量器材和体系的功能。
整体颤动(Total Jitter,简称Tj)为某误码率(Bit Error Ratio,简称BER)下颤动的峰峰值,在许多串行数据的标准中一般需求丈量误码率为10e-12的Tj,简写为Tj@BER=10e-12。 关于BER小于10e-8的Tj的丈量,一般只要误码率测验仪BERT能够直接丈量到。关于示波器,假定该高速信号为2.5Gbps的PCIe,单个 bit的时长为Unit interval = 400ps,假定示波器采样率为20G采样率,则1个bit上包含了400ps/50ps = 8个采样点,一次剖析1M个bit需求8M的存储深度,假如要丈量10个比特的颤动,需求让示波器在8M的存储深度下扫描100次,因为示波器在 8Mpts时核算颤动现已很耗时,重复100次的测验时刻会十分长。所以示波器丈量小于10e-12的误码率时的整体颤动有必要经过某些算法来预算Tj。
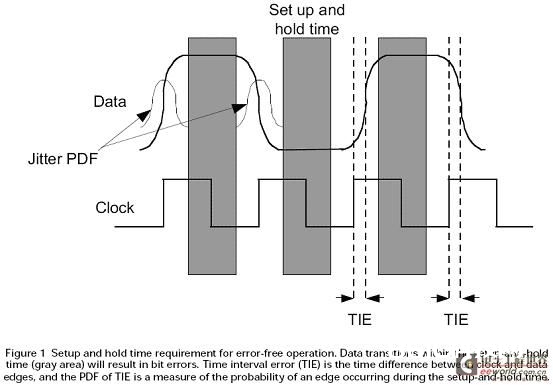
图1:TIE颤动图示与颤动概率密度函数(PDF)
基 于示波器求解颤动的算法一般在三个范畴调查和剖析,即时域、频域、核算域。比方TIE track即为TIE颤动在时域的函数;在频域剖析颤动的频谱,能够核算周期性颤动Pj和随机颤动Rj;TIE直方图、Tj的概率密度函数 (Probability Density Function,简称PDF)是在核算域来剖析颤动。
关于整体颤动的核算,一般从核算域剖析,即剖析颤动的直方图、概率密度函数PDF和累计散布函数(Cumulative Distribution Function,简称CDF)。
概率密度函数PDF的界说为:关于实数随机变量X,任何满意下列条件的函数都能够被界说为其概率密度函数 :
在下图2中扼要描绘了从TIE直方图生成PDF、CDF、浴盆曲线Bathtub curve的进程。
在第一步的图示中,X轴是颤动的值,Y轴是某个颤动值上的样本数量,示波器丈量每个信号每个边缘与参阅时钟的误差(即TIE),核算在某个颤动值上边缘的数量,得到TIE的直方图;
第二步中对直方图做归一化,即直方图中每个方柱子的数量除以样本总数,得到每个颤动值的产生概率,在这一步中即可得到TIE的概率密度函数PDF;

图2:颤动的直方图与PDF
在第三步中,对PDF的直方图从左右两头向中心进行积分。假定信号边缘相对抱负方位超出间隔x时,或许导致误码,误码率是对%&&&&&%从x到∞或-∞的积分(当x大于0时为∞,小于0时为-∞):BER(x) =1-CDF(x)。然后,对Y轴取对数后如下图3中深蓝色直方图。所示,因为测验样本较少,最矮的直方图的概率(即误码率)仅1%=10e-2,要核算10e-12的BER,需求对现有的BER直方图进行外插值;









