在数字信号处理中,丈量数据由于加法、乘法等运算位宽被扩展,可是资源利用上的考虑,在精度和差错有用范围内后续的处理并不需要这么大的位宽,因而对数据进行切断或许舍入处理是很有必要的。如图1所示为Xilinx FIR IPCore的参数装备界面,在FIR滤波器完成中必不可少的便是乘累加运算了,因而输出必有舍入处理,如图中Output Rounding Mode选项中就有很多种舍入算法。
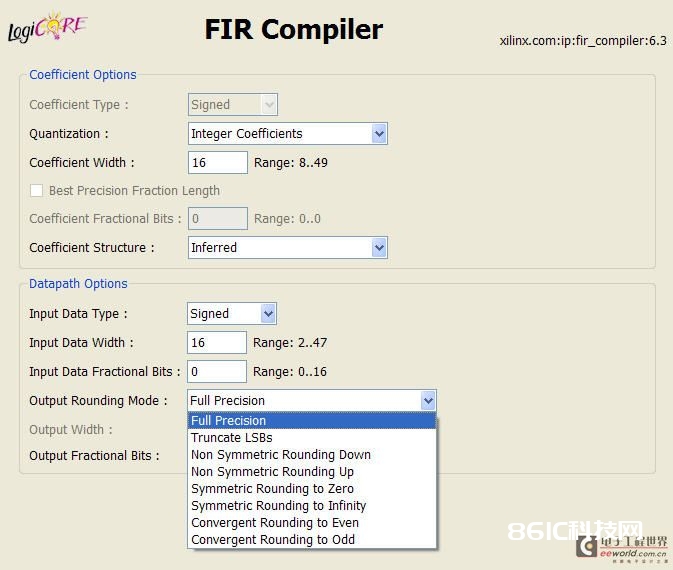
图1
关于舍入算法有多种,主要有Round Toward Nearest、Round Ceiling、Round Floor和Truncation:
Round Toward Nearest
Rounding Toward Nearest便是一般所说的“四舍五入”,以5为有符号数为例,高3位为整数位(包括最高位符号位),低2位为小数位。如图2所示,对5为有符号二进制数进行了舍入处理,舍去小数位,其间小数位大于0.5,整数位进1,小于0.5时不进位,而等于0.5时,舍入后数据打了问号,由于关于0.5的舍入处理,又可分为4种处理算法:
(1). Round Half Up;(2). Round Half Down;(3). Round Half Even;(4). Round Half Odd
而且以上第(1)、(2)种算法对应别离有对称(Symmetric)和非对称(Asymmetric)2类。
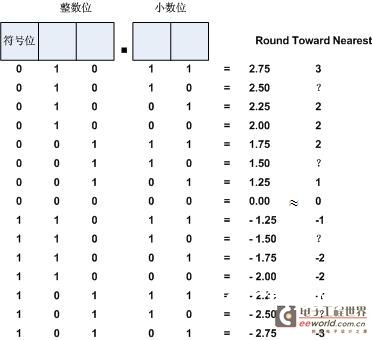
图2
(1). Round Half Up
Round Half Up算法关于0.5的舍入处理为向上取值,因而此例中整数位进1,而这仅对正数部分而言,关于负数部分可按照相关于0对称与否分为2类,如图3所示。
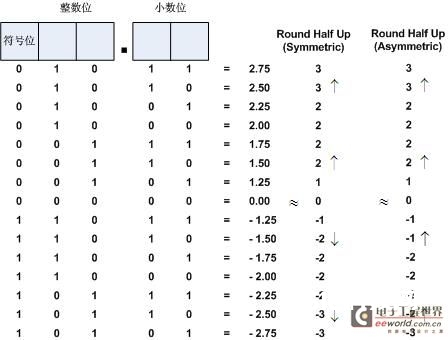
图3
(2). Round Half Down
Round Half Down算法关于0.5的舍入处理为向下取值,因而此例中整数位不进,而这仅对正数部分而言,关于负数部分可按照相关于0对称与否分为2类,如图4所示。
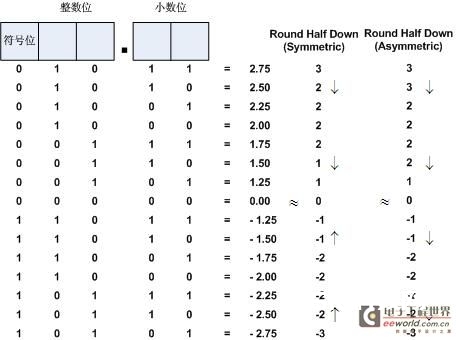
图4
(3). Round Half Even
Round Half Even算法依据有用位来判别是否进位,在此例中,舍去小数位,因而判别整数位即可,假如整数位为偶数,则不进位,奇数则进位,因而舍入处理后整数位肯定是个偶数。如图5所示,能够发现Round Half Even必定是Symmetric算法。









