高速公路微观动态交通流模型以交通流的集总行为为研讨目标,描绘了交通流的空间散布及随时刻改变的规则,能较精确地描绘高速公路交通流的实在行为,不只是交通自动操控系统规划、剖析、仿真决议计划的根底,也是交通预告和点评某些交通设施规划所需求的。其间,希腊学者Markos Papageorgiou所提出的Papageorgiou模型,能够以较小的核算量和满意的精度描绘车道数目单一、收支匝道无特大流量冲击的高速公路交通状况而广泛使用。
对交通流模型进行在线仿真,或验证某算法对实践路途的操控作用时,有时因为交通数据巨大或操控算法过于杂乱,往往耗费很多机时。尤其在外场环境下操作,工控机不只体积、功耗巨大,还易呈现作业异常的现象,在交通操控的实践使用中体现欠佳。FPGA技能高速、低本钱、小型化的优势使其理论研讨与实践使用成为炙手可热的研讨课题,现在现已彻底具有数据运算、信息处理、滤波核算等功用,常常使一些本来比较难处理的技能瓶颈得以轻松完成,从而使产品的可移植性增强,开发周期大为缩短,性价比大幅进步,一起FPGA能够完成纯硬件浮点运算功用,战胜定点数据对高精度、数据规模较大的运算力不从心的缺点,更适合科学与工程核算。因而本文选用浮点数在FPGA上完成Papa georgiou模型的仿真。
1 高速公路交通流微观动态模型
微观动态交通流模型又称为交通流连续介质模型,它经过对单向运动的交通流在某时刻t在某一方位x的有关变量来掌握交通的实质。各研讨安排所提出多种办法交通流模型,其间首要不同在于交通流量、车辆平均速度和车流密度的联系的表征,以及上下游交通相互作用的描绘办法。为了简化模型使其便于使用在实践中,一般依据高速公路几许形状和交通状况将其区分红若干路段,路段可不等距区分,但应确保每段路段车道数目相同,至多有一个进口、一个出口,每个路段的几许形状大致类似,每个路段内的交通状况近似均一,Papageorgiou模型也选用如图1所示的分段办法:
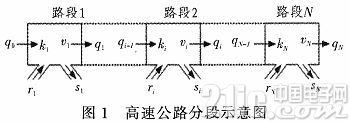
依据上述高速公路的分段办法,其数学表达式如式(1)~(4)所示:
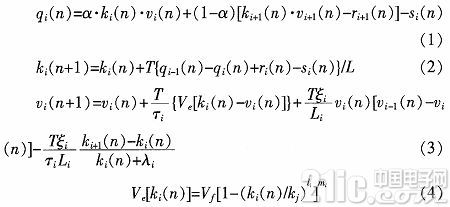
式(1)~(4)别离是动态流量模型、动态交通流密度模型、动态速度模型和速一密联系模型,各符号意义见文献。上述模型触及到了加减乘除及幂运算,现在Quartus II中有揭露的浮点数运算IP核可完成加减乘除运算,但式(4)中呈现有底数、指数或许均为浮点数的幂运算。本文依据所选参数进行多项式拟合,将一切运算均限定在加减乘除的浮点数运算规模内。
2 16位自定义浮点数数据格局
Quartus II软件自带的IP核的输入输出数据选用IEEE754单精度32位浮点数格局,其数据结构表明如下:
其间S为1位符号位,E为8位阶码位,M为尾数的24位小数位。调用QuartusII浮点数运算IP核完成加减乘除的操作,其资源耗费顺次为加减运算耗费LE单元个数均为1 497,耗费嵌入式乘法器个数均为0:乘除运算耗费LE单元个数别离为809、3345,耗费嵌入式乘法器个数别离为0、7。对一个路段进行仿真时,至少需求6次加法、7次减法、12次乘法、4次除法,仅完成加减乘除运算所耗费FPGA逻辑资源已蔚为壮观,若要仿真多个路段,将支付巨大的硬件本钱,乃至无法完成,因而本文在IEEE754浮点数格局的根底上选用自定义16位浮点数格局,编写浮点运算模块,尽量削减FPGA资源的耗费,其数据结构为:

其间S为1位符号位,E为6位阶码位,M为尾数的9位小数位,躲藏整数位1,其表明的数据值下式所示:
上式中,当S为0时,A为正数,当S为1时,A为负数;E-31为浮点数的指数,指数可在2-31到231之间改变;尾数选用原码表明,整数部分1为缺省值,不在上述格局中表明;0在上述格局中,阶码和尾数均为0,符号位能够是恣意值。为便利阐明自定义浮点数的运算进程,设有两个浮点数是a和b,其数据格局如式(6)所示。
2.1 自定义16位浮点数加法和减法运算
浮点数加、减法的操作进程类似,流程图如图2所示。
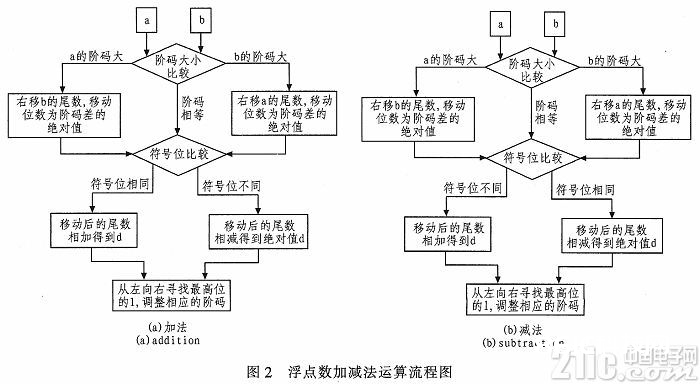
1)对阶操作:在两数尾数的小数部分的高位补1,比较两数的阶码是否相同。若相同,直接进入第2)步;若不同,比较两个数的阶码巨细,令阶码小的尾数连同高位补的1向右移位,右移的尾数等于阶差的绝对值;
2)符号位操作:加法运算,若两数符号相同,则符号位同两加数;若两加数符号相异,符号位由绝对值较大的加数决议。减法运算,被减数和减数的符号相异,则两数的绝对值相加;两数符号相同,则两数相减再取绝对值。成果的符号位取被减数的符号位(当被减数的绝对值较大时)或者是减数的符号位取反(当减数的绝对值较大时);
3)归一化操作:若进程1)和2)所得成果为非规格化数,找出运算成果的最高位1,由高至低顺次将其后部分存入终究成果,阶码做相应的调整。
2.2 自定义16位浮点数乘法和除法运算
浮点数的乘法运算依照以下进程进行,其算法流程图如图3所示。
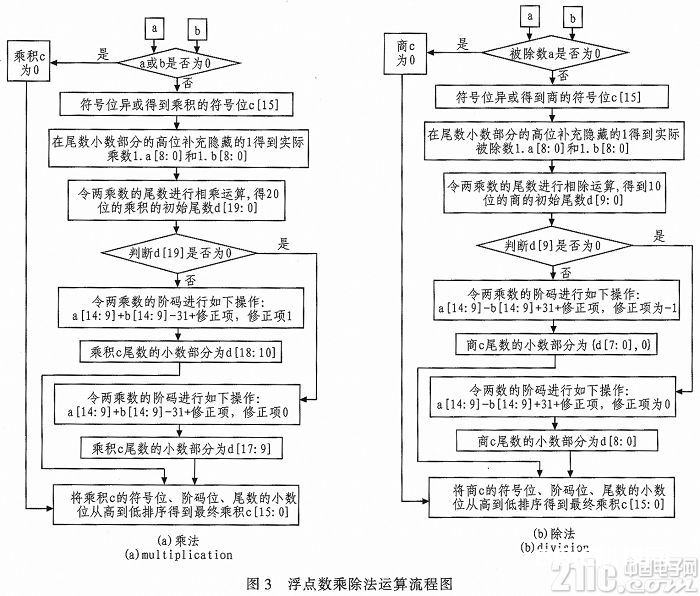
1)判0操作:乘法运算,检查两乘数是否有0,若有,成果为0。除法运算,检查被除数是否为0,若为0,成果为0。
2)符号位操作:对两数的符号位进行异或操作,确认成果的符号位。
3)阶码操作:乘法运算,乘积的阶码是(Ea+Eb-31+修正项);除法运算,商的阶码是(Ea-Eb+31+修正项)。修正项的值由4)中非规格化数调整为规格化数进行的移位个数决议。
4)尾数操作:乘法运算,两乘数尾数的小数部分的高位补1后相乘,得到乘积的20位初始尾数d;除法运算,被除数和除数尾数的小数部分的高位均补1,对1.Ma和1.Mb进行相除操作,令d=1.Ma÷1.Mb,选用移位相减,先比较1.Ma和1.Mb巨细,若1.Ma≥1.Mb,则d为1,且令1.Ma=1.Ma-l.Mb;若1.Ma1.Mb,则d为0,且令1.Ma左移一位再次进行比较得到d,顺次重复上述比较进程终究得到商的初始尾数d。
5)归一化操作:乘法运算,d[19]、d[18]不一起为0,若d[19]为0,即乘积的整数为01,则乘积尾数的小数部分为d[17:9],修正项为0;若d[19]为1,即乘积的整数为10或11,则将初始尾数右移一位,一起乘积指数加1,修正项为1,乘积尾数小数部分为d[18:10]。除法运算,d[9]和d[8]不会一起为0,若d[9]不为0,商的商的初始尾数的整数为1,尾数小数部分为d[8:0];若d[19]为0,商的初始尾数的整数为0,则将初始尾数左移一位,一起商的阶码减1,修正项为-1,商的尾数小数部分为d[7:0]并在低位补0。
将上述操作完毕后得到的符号位、阶码位、尾数的小数部分依照自定义浮点数格局进行摆放,得到终究的成果。
3 自定义浮点数运算的仿真机归纳剖析
为了验证本文中自定义浮点数运算模块的正确性及其差错巨细,且考虑到仿真模型中的变量都为正的浮点数,这儿以实数7.8和5.6为例,别离将其变换为本文中自定义的浮点数格局,在自行开发的以EP3C80E484C型号为中心的FPGA上运转,并经过QuartusⅡ软件中自带的debug工具软件检查其运算成果,其间加减乘除运算的部分成果如图4所示。
为了验证FPGA实践运算成果的正确性,将上述浮点数格局的成果转换成十进制格局,并进行系统差错比照,如表2所示。

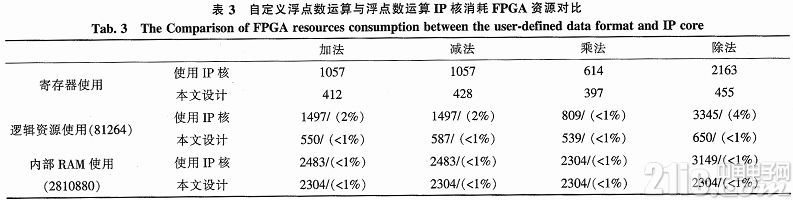
由表2的比照成果可知,在FPGA运转的16位自定义数据格局的加、减、乘、除运算模块的核算差错不超越0.1%,能够满意微观交通流模型的仿真中对核算精度的要求。此外,在确保模型仿真精度的一起,自定义16位数据格局的加、减、乘、除运算模块与Quartus II软件揭露的32位浮点数运算IP核比较,能够明显下降对FPGA资源的耗费,其资源比照如表3所示。
4 模型仿真及归纳剖析
依据自定义浮点数运算模块,前文以Papageorgiou模型为仿真目标,在FPGA上规划了交通流仿真模块。以一段长度为5 km的单向单车道的高速公路为例,将其等分为10段,选用时刻设为T=15 s,模型中其他参数设置为:α=0.95,ζ=1,l=1.86,m=4.05,τ=0.005 56 h,ζ=35 km2/h,λ=40 veh/km/lane,Vf=95.1 km/h,kj=110veh/km/ lane。
在初始时刻,假定各路段密度、速度相同,别离为60 veh/km/lane、30 km/h,并假定驶入高速公路的车流量为恒值Q0=1 500 veh/h,每个进口匝道车流量也为恒值r=750 veh/h。
在FPGA上对高速公路微观模型进行仿真需求留意两个问题:1)鸿沟赋值问题,这儿选用边际赋值条件,令v0(n)=v1(n),k0(n)=Q0/v1(n),k11(n)=k10(n);2)经过多项式拟合办法简化式(4)中指数和底数均为浮点数的幂运算,并由(7)式进行替换。
Ve[ki(n)]=0.008[ki(n)]3-0.064[ki(n)]2+0.371 4[ki(n)]+92.310 3 (7)
FPGA完成的模型仿真成果如图5所示。
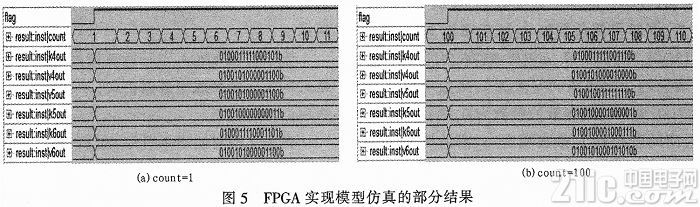
其间flag表明成果输出标志,count是仿真时刻距离的个数,k5out-k6out和v5out-v6out别是第5、6路段的交通流密度和车辆平均速度。为查验FPGA的仿真精度,选取count= 1,100时两组数据,转换成十进制浮点数办法,与MATLABA仿真成果比照,如表4所示。
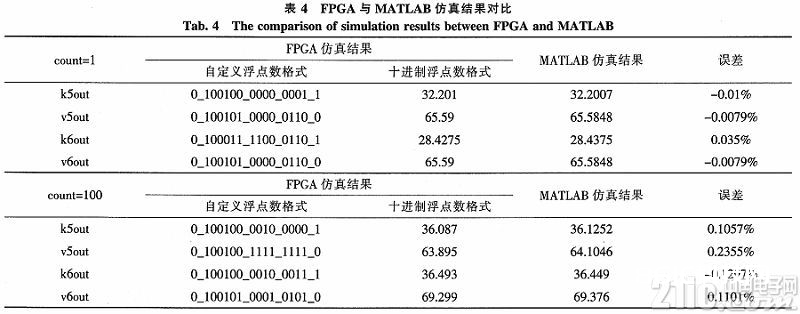
从表4知,依据FPGA的模型仿真与MATLAB的仿真成果比照,在仿真初期差错简直为0,跟着仿真时刻持续增长,差错随之增大,但整体距离不大,能够满意仿真精度的要求。
5 完毕语
1)本文规划了依据自定义浮点数的高速公路交通流微观动态模型仿真,并在自行开发的FPGA电路板进步行了验证,其间自定义浮点数运算完成简略,节省了FPGA逻辑资源,能够在确保核算精度的前提下以较快的速度完成模型的仿真,在后续的交通操控研讨中能够进一步在FPGA上完成操控算法的作用验证;
2)本文的不足之处在于没有直接完成底数和指数全为浮点数的幂运算,而是依据所设定的参数进行多项式拟合,导致模型仿真精度在必定程度上遭到拟合精度的约束。