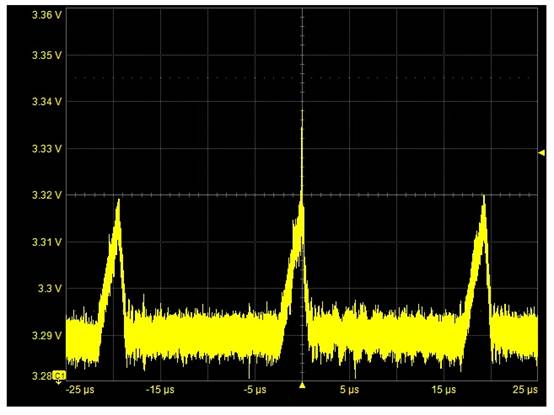
数字示波器中供给的采样率,特别是在长波形捕获时刻的示波器中,一般要远远高于被剖析的信号频谱实践要求的采样率。这种过采样能够作为一种优势,对数字化信号滤波,以进步显现的曲线的有用分辨率,或去掉不想要的噪声。
I. 增强分辨率
增强分辨率函数运用有限脉冲呼应(FIR)滤波器,其与运用简略的均匀滤波器滑润信号相似,但带宽功率更高,具有更好的带通特色。在均匀接连曲线具有重要意义。 关于信号具有单次特色(信号不能重复,或不能设置安稳触发)而不能运用均匀函数时,能够运用这一函数。
a. 增强分辨率的优势
增强分辨率(ERES)滤波改进了仪器具有两个特色:
1. 在任何状况下,每个滤波器运用固定数量都会改进分辨率(即区别相距很近的电压电平的才能)。不论信号是否有噪声,是单次信号仍是重复信号,这都能够有用进步分辨率。
2. 能够改进信噪比(SNR),详细取决于原始信号中的噪声方式,因为增强分辨率滤波会下降信号带宽,从而滤除部分噪声。
b.力科示波器中的增强分辨率
力科DSO完成了一套线性相位有限脉冲呼应(FIR)滤波器,这些滤波器是为供给快速核算、完美的阶跃呼应、及以0.5位步长在0.5-3位之间改 善分辨率、一起使带宽下降最小而优化的。每个0.5位步长对应两倍的带宽下降,能够简洁地操控带宽/分辨率之间的对立。下表是这些示波器中供给的六种滤波 器的参数。

运用的滤波器是低通滤波器,因此在详细状况下SNR的实践进步程度取决于信号上存在的噪声的功率谱密度。假如信号中的噪声是白噪声,即均匀散布在频 谱中,滤波器改进SNR的程度与其改进分辨率的程度相同。假如噪声功率倾向高频,那么SNR改进程度将好于分辨率改进程度。假如噪声首要散布在较低的频率 上,那么SNR改进程度可能会低于分辨率改进程度。因为去掉相干噪声信号而改进SNR的程度(如时钟信号馈通)取决于信号是否坐落滤波器的传输频带中。通 过运用数字示波器的频谱剖析选项,能够简洁地导出成果。
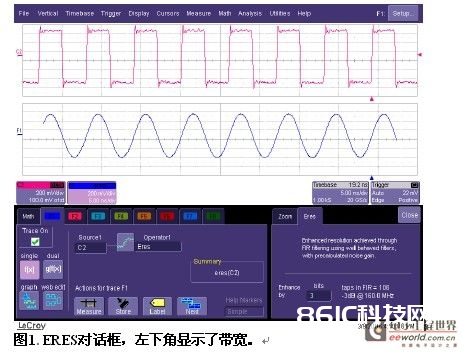
增强分辨率对话框(参见图1)能够帮忙用户为详细运用挑选恰当的滤波器,标明ERES滤波器的-3 dB带宽是与当时波形的当时时基设置对应的实践频率。
增强分辨率函数运用的滤波器具有彻底线性相位呼应,它有两个所需的特色:榜首,滤波器不会使波形中不同事情的相对方位失真,即便事情的频率成分不同。第二,在核算滤波的波形过程中,能够彻底补偿与滤波有关的正常推迟(输入波形和输出波形之间)。
II. 什么时候应该运用增强分辨率?
特别合适增强分辨率的首要状况有两种:榜首,假如信号的噪声显着很高(且不要求丈量噪声),那么能够运用增强分辨率函数“铲除”信号。第二,即便信号噪声不太高,但要求对波形进行高精度丈量(可能在高笔直增益的状况下运用缩放),那么增强分辨率将进步丈量的分辨率。
从全体上看,在数据记载具有单次特色或低速重复特色、不能运用均匀函数的状况下,增强分辨率能够替代均匀函数。
下面的实例介绍了在这些状况下运用增强分辨率函数。
III. 滤除噪声
图2显现了增强分辨率对有噪声的信号的影响,上图显现的是带有噪声的阻尼正弦曲线。下图显现了在3位分辨率增强后的同一信号。现在能够清楚地看到较 低电平的振动,能够对感兴趣的信号进行频率、起伏或周期等丈量。在频域中检查的同一信号显现了增强分辨率函数的低通滤波影响。图3显现了图2中的信号的功 率谱。上面的一对曲线显现了输入波形和没有滤波的信号的频谱,下面的一对曲线则显现了3位分辨率增强后的信号和信号频谱。3.0位增强滤波器具有200 kHz的-3 dB带宽。在超越这个频率时,滤波器从信号中去掉能量。
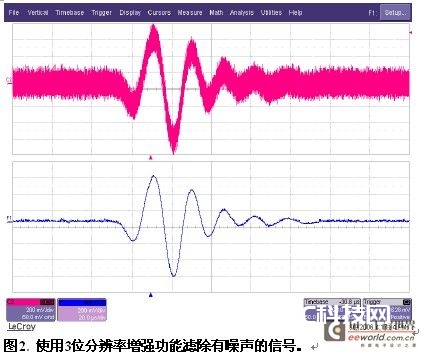
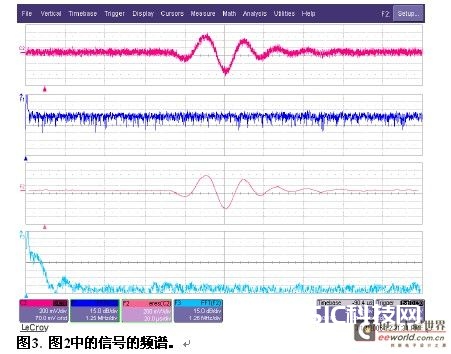
图4是增强分辨率的另一个作业视图。咱们调查了收集的正弦涉及进行3位增强分辨率处理后正弦波的直方图。上面的直方图表明通道2中的波形每个样点的 电压起伏。这是8位数据,在运用显现的2000个二元组制作直方图时,因为8位数字化器的分辨率有限,显现了象鸡冠相同的外观。