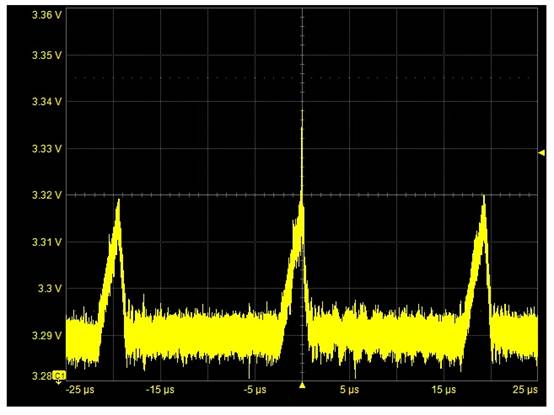
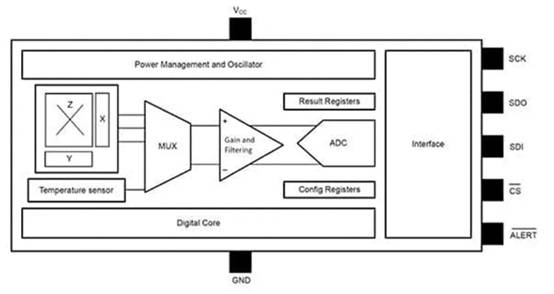
怎么才能使 A/D 转化器完结最高功用呢?显着的答案便是选用杰出的规划和板面布局,除此之外,咱们还可选用其他技能取得功用进步。咱们实践上可选用一些简略的技能来推进 A/D 转化器功用,使之优于标准的要求。为了完结这一点,咱们应了解 A/D 转化器差错的来历和类型。
本文的意图是解说 A/D 转化器最常见的差错源,并介绍进行上述差错补偿的办法。某些差错补偿的办法了解和施行起来都比较简略,而有些办规律不那么显浅易懂。假如选用办法妥当的话,上述办法可大幅进步体系全体功用。
咱们无妨先来看看抱负的 A/D 转化器应该是什么样的,了解哪些类型的差错会阻止咱们取得最佳功用。简而言之,抱负的 A/D 转化器会为咱们供给简直抱负的数据。我说简直是抱负的,是由于即使抱负的 A/D 转化器也存在量化差错,但咱们无妨今后再评论这一点。咱们希望进步 A/D 转化器的功用,所以咱们无妨先来看看市场上分辨率最高的 A/D 转化器,即 24 位 A/D 转化器。
抱负的 24 位 A/D 转化器可供给 24 位可用数据。这种 A/D 转化器可为给定输入供给相同代码或转化成果的输出,相同也遭到量化的约束。例如,假如咱们对输入规划为 5.0V 的抱负的 24 位 A/D 转化器选用刚好 2.5V 的固定模仿信号,那么咱们从 A/D 转化器所得的仅有代码便是8,388,608–标度值 (scale value) 的一半。假如咱们对非抱负转化器选用相同电压的话,那么输出代码不会固定为一半巨细值,它实践上会给出不同的输出,是否安稳并不确认,这是由转化器的不抱负特性形成的。不抱负的 A/D 转化器会形成量化差错、偏移和增益差错以及非线性。此外,噪声和漂移也会导致丈量差错。
即使是抱负的 A/D 转化器也会发生量化差错。量化差错指数字化模仿输入信号时发生的差错。举例来说,输入规划为 5V,那么每个代码反映约 298 nV (5V/2^24) 的分辨率。假如咱们开始时选用 0V 模仿输入电压,然后再逐渐添加模仿输入电压,那么代码会坚持零不变,直至到达 149 nV 或 ? LSB 左右进行第一个代码转化。因而,即使选用抱负的 A/D 转化器,咱们仍会遇到 +/- ? LSB 的量化差错。之所以如此,是由于模仿输入信号在 0V 到 149 nV 之间可取一个无限数值,但数字代码只能为有限数值,抱负状况下仅为 0。
咱们常常同时考虑偏移差错和增益差错。偏移差错是指对 A/D 转化器选用零伏差动输入时实践代码与抱负代码之间的差异。增益差错是指从负满量程转为正满量程输入时实践斜率与抱负斜率之差。偏移和增益差错一般是 A/D 转化器中首要的差错源。
非线性包含整数非线性 (INL) 和差动非线性 (DNL)。整数非线性指出的是输出代码与抱负输出之间差异的巨细,而偏移和增益差错已得到校对。在满量程端点 (full-scale endpoint) 处取一抱负线,一般来说,经丈量得到的 INL 既为到这一抱负线的最大差错。差动非线性是指代码值怎么随模仿输入的改变而改变。就模仿输入电压的升高状况而言,代码或许添加、不变或削减。依据模仿输入增量的多少,代码应该坚持不变或许添加。假如呈现这种状况的话,那么 ADC 便是单调性的。假如 ADC 越过一个输出代码,那么此代码称之为缺失代码。假如代码输出削减,那么咱们就说 ADC 为非单调性。经过查看柱状图,咱们可以得知是否存在缺失码,以及联系代码宽度的巨细等。假如分配正常而无缺失码,那么这就标明代码宽度共同。
噪声是随时刻改变的随机输出代码,与偏移、增益和线性差错无关。即使咱们现已很好地校对了A/D 转化器的一切其他差错来历,咱们仍会发现由于噪音的原因呈现输出代码改变。
漂移是指在给定输入的状况下输出代码随时刻或温度的改变而进行的改变。假如咱们选用固定的模仿电压,然后给设备加热或去热,输出代码就会跟着温度而进行偏移。依据设备特性的不同,在给定的抽样中漂移或许向相同方向开展,也或许呈随机性。
虽然难以对一切差错来历进行可视化,不过咱们可经过芯片级规划技能或数据处理技能来处理这些差错来历。在咱们具体了解怎么补偿差错源之前,无妨先来了解一下A/D架构。在分辨率大于16位时,咱们广泛选用 Δ-Σ 架构。Δ-Σ 架构选用重复采样技能来完结高分辨率数字输出。图 1 给出了简化的 Δ-ΣA/D 转化器结构图。A/D 的首要组件是调制器和滤波器。调制器作为反应环路环路作业,其方针是将差动信号差错驱动为零。咱们经过微差丈量模仿输入信号和反应DAC信号来完结这一意图。Δ-Σ 架构中的Δ(delta) 因而得名。上述二者之差或信号差错结合或算计到下一级。Δ-Σ 架构中的西格玛由此而来。将总差错与参照信号相比较,然后相应地设置比较器的输出。假如差错项为正值,则反应 DAC 输出升高,以测验减小差动差错项。假如差错项为负值,那么反应DAC 输出则下降,以测验减小差动差错项。比较器 1 和 0 的密度与模仿输入电压成正比。
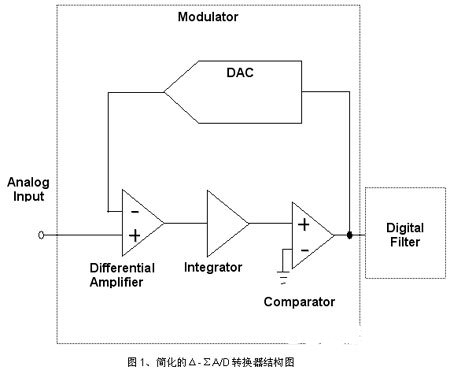
上述架构十分适用于高分辨率运用,因而咱们无妨看看上述架构中各种类型的差错源是怎么露出出来的。
咱们可经过选用噪声整形技能使Δ-Σ架构中的量化差错到达最小。噪声整形技能不会减小或消除量化噪声;它仅仅将量化噪声面向更高频率、使之不再影响有关频率(低频)罢了。因而,就量化噪声而言,Δ-Σ架构的规划可以将量化噪声的影响降至最低。
Δ-Σ架构中存在偏移和增益差错,这与任何其他数据转化器的状况相同。此外,正是由于与任何其他数据转化器的状况相同,因而咱们也可以经过简略的校准技能将上述差错最小化。为了进行偏移校准,咱们选用 0V 或十分小的信号并读取输出代码。假如成果为正,那么转化器就存在正偏移差错,咱们从成果中减去偏移值;假如成果为负,那么转化器就存在负偏移差错,咱们就向成果加上偏移值。
咱们经过对A/D转化器施加满量程或近于满量程的信号并丈量输出代码来完结增益校准。偏移校准在增益校准之前进行。假如作图显现A/D转化器的一切输出代码的话,咱们看到增益差错与抱负输出代码斜率发生违背,因而增益批改只不过是调整这条线的斜率罢了。
INL存在于Δ-Σ架构中,就像任何其他数据转化器相同。可是,咱们可以经过后处理数据对它进行补偿。从理论上说,INL 可以逐一代码地进行校准,但这是不实践的,因而一般咱们挑选一些数据点来校对 INL。咱们经过对表进行线性化来完结上述作业。
DNL一般对Δ-Σ架构而言不是问题。就其特性而言,反应环路中1位DAC输出是线性的,因而架构不调整也能取得优异的DNL功用。
任何电子设备都存在噪声,无法消除,但咱们可以评论选用何种办法来减小这种差错源。
任何电子设备都存在温度漂移,无法消除,不过,假如可以估量漂移的话,那么咱们就能经过线性化表来补偿其影响。咱们可经过温度监测来完结上述意图。此外,咱们还能很精确地确认漂移对体系功用的约束。
因而,总而言之:咱们可经过噪声整形技能来操控Δ-Σ架构中的量化差错,经过校准来最小化偏移和增益差错,选用线性化来改进 INL,而 DNL 则简直不存在,噪声可最小化,而漂移则可纠正,其影响也可以估量。
最小化噪声要比偏移和增益校准杂乱一些。电子电路中有许多噪声源:热噪声、1/f 闪耀噪声和突发噪声。在最小化噪声方面,噪声类型十分重要。热噪声从实质上说是高斯型的,因而咱们可选用特定技能来最小化其影响。闪耀噪声和突发噪声从实质上说对错高斯型的,因而上述技能对处理这种噪声源没有用能。
咱们在评价噪声前,无妨先来看看噪声与分辨率之间的联系。噪声和分辨率互相相关,互相界说。噪声可界说为输出代码与抱负代码间的随机差错。一般噪声的表现形式是伏特、代码、数量或PPM,而分辨率单位一般为位数或 dB。为了阐明这一点,咱们无妨假定抱负的 24 位 A/D 转化器具有5V模仿输入规划。明显,分辨率为24位,由于这是抱负状况。假如咱们用 dB 来反映分辨率的话,那么分辨率便是6.02 * N dB(这儿的 N 是位数),即 144.5 dB。咱们一般称这种界说为信噪比。假如咱们用代码来标明噪声,那么噪声便是一个代码。假如咱们用计数来标明噪声,那么它便是 16,777,216 次计数。假如咱们用伏特来标明噪声,那么它便是 (1/16,777,216) * 5V,即 298 毫微伏。假如咱们用 PPM 来表达噪声,那么它便是 1/16,777,216 PPM,即 0.06 PPM。
这提出了另一个问题,非抱负A/D转化器的分辨率怎么界说?“有用位数”(ENOB) 和/或“有用分辨率”等术语一般用于界说A/D转化器的可用分辨率,假如考虑到设备的噪声约束的话。为了有助于了解分辨率和“有用分辨率”或ENOB之间的差异,咱们无妨先看一下抱负的12位A/D转化器。抱负的12位A/D转化器有4,096个代码,也便是说分辨率为244 PPM。假如将模仿输入转化为数字值时咱们强制给转化器成果添加12位分辨率,那么咱们就可以说咱们取得了24位分辨率的A/D转化器。实践上只要12位有用。上面的比如或许并不像您想像的那么极点。例如,市场上实践出售的A/D转化器就号称是24位A/D。在大约 25 Hz 的数据输出速率时,其噪声约 0.4 PPM,就其自身而言是适当不错的。可是,0.4 PPM的噪声意味着只要大约21.3位的有用分辨率。谁动了咱们的24位分辨率?此外,假如您进步采样率,那么噪声或许会超越 600 PPM,这就使其乃至比 12 位 A/D 还糟糕!
有没有或许完结实在的 24 位功用呢?答案是必定的。不过咱们要做好准备作业。走运的是,咱们可用各种技能来减小A/D转化器的噪声。此外,假如咱们体系有搅扰的话,那么咱们也可选用相似的技能来减小或消除它。从实质上说,咱们可使 A/D 转化器取得更高的实践分辨率位数,然后完结更高的全体体系功用。这便是归纳各种技能的优势地点。
为了完结更高功用,咱们有必要了解 A/D 转化器功用有多强。一项确认 A/D 转化器功用的广为选用的技能便是进行柱状图剖析。柱状图可清楚地告知咱们A/D转化器在DNL、DC偏移和噪声方面的状况。柱状图显现了输出代码和输出代码呈现次数之间的比照状况。从柱状图测验中,咱们可评价出代码宽度或容量巨细 (DNL)。经过将输入接地,咱们或许评价出噪声方面的信息。假如A/D转化器DNL较好,噪声为白噪声,那么柱状图就应相似于高斯型或正常散布。假如代码宽度小,那么代码呈现的就少;假如代码宽度较大,那么代码呈现就较多。假如代码不呈现,那么就标明代码缺失。柱状图剖析可以成为一种十分强壮的东西。咱们可方便地了解 DNL 功用和噪声特性。
假如柱状图显现 DNL 功用较好,散布也正常,那么咱们就可假定噪声为白噪声。由于咱们调查的是Δ-ΣA/D 转化器,因而从界说而言差动非线性应满足。ADS1252 Δ-Σ A/D 转化器的数据采样柱状图为 32,768,这标明 DNL 功用近于抱负状况,而输出代码散布与正常散布很相似。因而,咱们可以假定该 A/D 转化器的噪声为白噪声。这意味着咱们可运用核算学办法来评价噪声。
如前所述,假如A/D转化器数据有一般的特性形式,那么咱们可将数据集放入一般形式中。一般形式一般是指概率散布。由于数据表现出白噪声特性,因而咱们可用高斯机率密度函数来评价噪声。函数显现了信号超出特定值的或许性,如以下方程所示:

这儿:
u =实在均匀数
x =信号值
s =标准差错
从该方程式可看到,跟着 x 从均匀值移开,或许性下降,而输入信号会超越给定值。运用该方程式,咱们可实践核算信号在给守时刻内处于特定规划的或许性。
因而,咱们可选用高斯几率密度函数作为数据模型。下一个问题便是咱们的模型究竟有多好?咱们用两种标准核算原理来处理这一问题。首要,均匀规律指出,假如整体存在一个实在的均匀数 (u)且x为整体中n个个别随机采样的采样均匀数,那么跟着n不断加大,采样均匀数 (x) 也会越来越挨近实在均匀数 (u)。由于咱们评论的是白噪声的状况,因而采样均匀数会与实在均匀数很挨近,条件是采样规划满足大。因而,咱们知道咱们可以信赖核算得出的实在均匀数 (u),由于它与实在均匀数 (u) 有关。
咱们怎么了解标准差错核算得究竟好不好?咱们可用中心极限定理来答复这一问题。该定理指出,假如整体具有实在均匀数 (u) 和实在标准差错 (s),那么整体中n个个别一切或许的采样均匀数调集的概率散布就会随n的增大越来越挨近均匀数 (u) 和标准差错 (s/sqrt n) 的正常散布。从根本上说,假如咱们采样更多的话,那么咱们就能减小标准差错。
假如咱们彻底依靠中心极限定理,那么咱们可选用越来越多的采样,然后使标准差错越来越小。不过改进的速度不会太快。采样数量添加完结标准差错改进也有一个约束。一旦采样数超越了这个约束,那么您就不会再得到任何优点,乃至还会添加标准差错。采样数量有约束的理论树立在方差的根底之上。方差理论广泛用于评价信号源的频率安稳性,不过它适用于任何采样体系。换言之,体系安稳时采样只会下降标准差错。安稳性受许多要素影响,包含随即事情,乃至体系中的漂移。
关于首要包含白噪声的体系而言(与咱们这儿评论的体系相似),均匀方差是标准方差的丈量办法。在这种类型的体系中,咱们可选用方差来估量标准方差。经过运用方差,咱们可实践估量采样对体系的影响。从根本上说,方差剖析之所以起作用,是由于咱们收集了很多采样并剖析采样数量上升时方差怎么改变。方差最小时的采样数量便是咱们给定体系的最佳采样数量。这是一个十分有用的东西,有助于咱们快速而方便地优化采样技能,然后取得最大的体系功用。
咱们无妨将理论运用到实践的 24 位 A/D 转化器来进行检测。咱们前面说到的 24 位 A/D 转化器在25 Hz 采样率上噪声约为 0.4 PPM。将 PPM 转化为位数,咱们可评价应当怎么对 A/D 转化器进行采样以取得希望的功用。在 PPM 和位数之间互相转化的方程式如下所示。
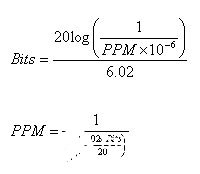
在 PPM 与位数之间互相转化的方程式
运用以上方程式时,为了取得 24 位分辩率,咱们需求将噪声下降至 0.06 PPM。这便是说,咱们有必要使噪声削减简直 7 个值才可以。依据中心极限定理,咱们需求选用约 49 个采样来完结上述噪声功用。不幸的是,这会让咱们的采样率降至约 0.4 Hz,而咱们的信号带宽(-3dB 频率)则降至约0.1 Hz。这种采样率不只关于许多运用而言太慢了,并且信号带宽也会对功用形成灾难性影响,由于输入信号的任何改变都会对树立时刻形成极大影响。咱们可以以更快的采样速率运转 24 位 A/D,但有用分辩率的下降形成的问题比信号速率还严峻,因而咱们寻求高速度反而会使问题恶化。
走运的是,咱们可以找到处理该问题的办法。ADS1252是一种采样频率为 40 kHz 的 24 位 Δ-Σ A/D转化器。假如有用分辩率在 40 kHz 速率上满足高,那么咱们就可取得满足的分辩率,可以对数据进行采样以进步分辩率,并依然可取得满足的采样率。咱们无妨来看看 ADS1252 的标准功用,其在 41,667 Hz 数据速率上的噪声为2.5 PPM。依据中心极限定理,咱们应选用 1,736 个采样来完结 0.06 PPM 的噪声,这时的数据速率为 24 Hz。从论文上看,咱们已取得了处理方案。此外,由于咱们的 A/D 运转时选用更快的采样率,从均匀采样数来看,总滤波器衰减较慢。这意味着咱们可取得更高的信号带宽。例如,咱们新近谈到了带有 sinc3 滤波器的 25 Hz 的 24 位 A/D 转化器,其输出的信号带宽约为 6 Hz。选用均匀数据的 ADS1252 的信号带宽约为 10 Hz,因而咱们实践上进步了信号带宽。
为了弄理解该处理方案是否切实可行,咱们收集了数以万计的采样,并选用均匀和方差技能来查看是否确有用果。表 1 和表 2 给出了不同理论的噪声和分辩率比较。
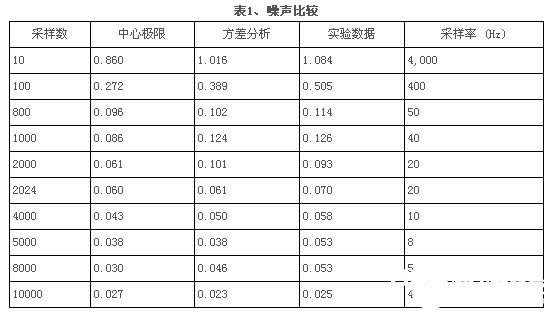

表中数据显现了一些风趣的成果。方差剖析与试验数据稳和很好;可是,试验数据与中心极限定理估量应得的成果则存在必定差错。这很或许是由于体系搅扰形成的。进一步剖析方差显现,采样大于 12,000 没有任何优点。对超越 12,000 次的采样进行均匀,实践上反而会下降噪声功用,由于体系因漂移而形成不安稳。因而,咱们选用本办法可对体系功用进行优化。
责任编辑:gt