0 导言
在高功用沟通传动体系中，速度闭环操控是必不可少的，即需求构成所谓的有速度传感器
沟通调速体系。但因为速度传感器的本钱、装置、保护、非线性和低速功用等方面的原因，并且有些场合不允许电机外装任何传感器，这就影响到了异步电机调速体系的简单性、廉价性及体系的可靠性。因而，无速度传感器的沟通电动机操控体系的研讨与开发就越来越遭到学者的重视。
无速度传感器操控体系的中心问题是对电机转子的速度进行估量。操控体系功用的好坏将取决于操控计划与速度辨识环节的规划。本文针对现在研讨较多的几种速度辨识办法进行了剖析，指出了各自的优缺点以及在工业运用场合的有用性。
1 不同速度辨识办法剖析
现在为止，在无速度传感器异步电机矢量操控体系中现已呈现了很多种速度辨识办法，大体可分为以下几种：动态直接估算法、模型参阅自适应(MRAS)法、自适应转速观测器办法、PI 自适应调节器法，依据神经网络的速度估量器以及转子齿谐波法和高频注入法。运用这些办法均可完成异步电机在无速度传感器情况下的操控运转。
1.1 动态速度估量器
无速度传感器技能发展的初期是依据电机稳态模型，推导出滑差频率的表达式。因为该办法的起点是稳态方程，因而调速规模小、动态功用差，无法满意高功用调速体系的要求。之后有学者依据电机的动
态派克方程，规划出了电机的开环动态速度估量器。
现在所见动态速度估量器主要有以下四种方式。
1.1.1 依据转子磁链的估量办法
存在如下问题:
第一个问题是需求抱负的积分器;
第二个问题是该办法对电机参数特别是对定子电阻的改变比较灵敏，这在低速时表现得特别显着;
第三个问题是PWM和死区效应的影响。
因而，完成对定子电压的精确丈量非常困难。
1.1.2 依据反电动势的估量办法
该办法经过以转子磁链反电势矢量的角速度，减去反电动势矢量与电机转子的相对角速度，得到电机转子的角速度。
该办法与依据转子磁链的速度估量器的思路相似，差异在于因为运用转子反电势代替转子磁链，因而去掉了纯积分环节。当频率挨近零时，式(3)中的分母和分子均变为零，因而选用此办法存在精确性问题。至于对参数的灵敏性，其缺点与前述的办法是相同的。
1.1.3 依据定子磁链的估量办法
该办法以定子磁链的角速度为基准，减去定转子磁链之间的相对角速度以及转子磁链与转子之间的相对角速度，得到电机转子的角速度。
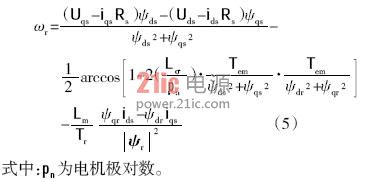
选用前述办法核算转子磁链的瞬时角速度时，需求核算转子磁链的微分。若依据定子磁链核算电机转速，便能够消除微分运算，可是又会引进运算量巨大的反余弦函数。
1.1.4 直接核算法
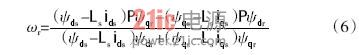
式中：P为微分算子。
从式(6)知，该办法的核算公式中彻底去掉了Rr和Rs项，提高了体系的鲁棒性，可是需求精确地丈量定子和转子磁链。因为公式中含有微分运算，并且其分子和分母项中包括相同的过零点，因而有必要借助于低通滤波器才能够完成其功用，因而这种计划并非非常有用。
1.2 依据MRAS的速度估量办法
模型参阅自适应体系要求操控体系用一个模型来表现，模型的输出便是抱负的呼应，这个模型称为参阅模型。体系在运转中总是力求使可调模型的动态与参阅模型的动态共同。经过比较参阅模型和实践进程的输出，并经过自适应操控器去调整可调模型的某些参数或发生一个辅助输入，以使得实践输出与参阅模型的输出差错尽可能的小。
将异步电动机在停止两相琢茁坐标上的电压模型作为参阅模型，电流模型作为可调模型，就能够规划出图1所示的转速自适应辨识体系框图。
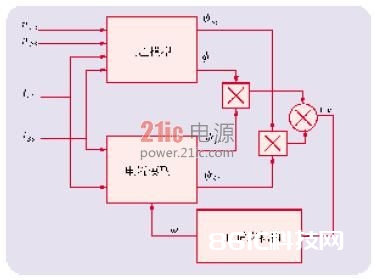
依据波波夫(Popov)超稳性理论可得自适应速度辨识公式
式中：Ki，Kp为积分常数。
式(7)中存在纯积分环节，为消除其影响，引进输出滤波环节，一起为了平衡输出滤波环节带来的磁链估量的相移差错，同样在可调模型中引进相同的滤波环节，算法如图2所示。
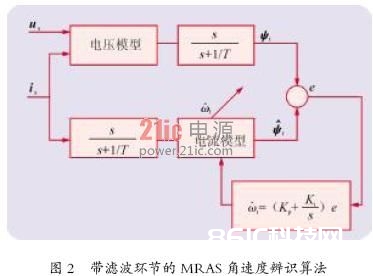
此算法没能处理电压模型中定子电阻的影响，低速的辨识精度也不抱负，这也就约束了操控体系调速规模的进一步扩展。对电流模型的两头进行微分可得反电动势的近似模型为
用反电动势信号替代磁链信号的办法去掉了参阅模型中的纯积分环节，改善了估量功用。但式(8)的取得是以角速度恒定为条件的，这在动态进程中会发生必定的差错，并且参阅模型中定子电阻的影响依然存在。
因为定子电阻的存在，使辨识功用在低速下没有得到较大的改善。处理的办法，一是实时辨识定子电阻，但无疑会添加体系的复杂性;二是能够从参阅模型中去掉定子电阻，选用无功功率模型。
1.3 自适应转速观测器
1.3.1 卡尔曼滤波技能(KFT)
卡尔曼滤波是由R.E.Kalman 于上个世纪60 时代提出的一种最小方差意义上的最优猜测估量的办法，是一种鲁棒性杰出的线性体系滤波器。当输入和输出信号被噪声所污染时，经过挑选合理的增益矩阵能够取得最优的滤波作用。
假如电机未装置速度传感器，电机停止的琢茁模型为一非线性方程，此刻就需求运用扩展卡尔曼滤波器进行转速估量。在扩展卡尔曼滤波运用中，一般分为两个过程。第一个过程称为预告阶段，该过程主要是核算状况量预告值和状况差错协方差预告值这两个量;第二个过程称为更新阶段，在该过程中即将核算出所结构的卡尔曼滤波器的增益，进行状况差错协方差矩阵的更新，还要对所预告的状况值进行更新。
该办法在动态进程中还存在着必定的滞后性，不能彻底满意高功用操控的要求。比较其它算法，卡尔曼滤波算法核算量很大。一起，这种办法是树立在对差错和丈量噪声的计算特性已知的基础上的，需求在实践中探索出适宜的特性参数。终究，该办法对参数改变的鲁棒性并无改善，因而，现在有用性上还不强。
1.3.2 全阶状况观测器办法和滑模观测器办法
前者实践上也归于模型参阅自适应(MRAS)法，只不过是以电机本身为参阅模型的，此处不作详细介绍;后者选用估量电流差错来确认滑模操控组织，并使操控体系的状况终究稳定在规划好的滑模超平面上。滑模操控具有杰出的动态呼应，在鲁棒性和简单性上也比较突出。但它存在颤动，当今许多学者正致力于研讨怎么去抖这一问题，并现已取得了较好的作用。
综上所述，选用自适应观测器是为了处理抗干扰的抗参数改变的问题，以上所提的办法不同程度上改善了这一功用，但体系也一起变得复杂。现在，具有实践意义的课题是研讨怎样在改善鲁棒性的一起尽可能简化辨识算法，尽管已有学者提出一些选用电机降阶模型的闭环观测办法，在体系复杂性上有所改善，但惋惜的是，整体的功用没有取得相当大的改善作用，在这一方面人们有许多工作要做。
1.4 依据PI 自适应操控器
这种办法适用于转子磁场定向的矢量操控体系，其基本思想是运用某些量的差错项，使其经过PI自适应操控器而得到转速信息。详细原理可由转子磁场定向下的电机派克方程推得。令
