本文提出了一种根据曲面L ED 阵列的光强散布数学模型的新式办法,在推导了曲面L ED 阵列光强散布数学模型的基础上,将其应用于L ED 摩托车信号灯配光规划。假如能够从理论上树立L ED 光强散布的数学模型,研讨一种L ED 阵列的光强散布且无需聚光器和配光镜,使其满意国家标准,从而为L ED 摩托车信号灯规划供给一种新的方便、有用的办法,具有重要的理论与实践指导意义。
1 曲面LED 阵列的光强散布的数学模型
1. 1 单个LED 光强散布的数学模型
首要树立单个L ED 光强的散布模型,如图1 所示。其间,勘探球面中心为(0 ,0 ,0) ,半径为r ,α表明L ED 光源的水平方向角;β表明L ED 光源的笔直方向角;θ表明单个L ED 光线OM 与光轴OL 的夹角;φ表明L ED 光轴OL 与其在x y 平面投影的夹角;γ表明L ED 光轴OL 在x y 平面投影与Y 轴的夹角。

则L ED 光轴对应的单位坐标为(co sφsinγ,cosφsinγ,sinφ) ,勘探球面上M点的坐标( rcosβsinα,rcosβcosα, rsinβ) 。
由此,L ED 光源的光强散布能够表明为I =I (θ) 或许I = I (α,β) 。
而单个L ED 的光强散布不是抱负的朗伯体,该散布能够表述为:
当θ =θ1/ 2 时
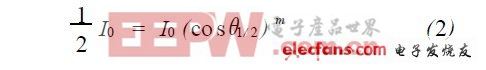
即