本文简明叙述GMM-HMM在语音辨认上的原理，建模和测验进程。
1. 什么是Hidden Markov Model？
HMM要处理的三个问题：
1） Likelihood
2） Decoding
3） Training
2. GMM是什么？怎样用GMM求某一音素（phoneme）的概率？
3. GMM+HMM大法处理语音辨认
3.1 辨认
3.2 练习
3.2.1 Training the params of GMM
3.2.2 Training the params of HMM
====================================================================
1. 什么是Hidden Markov Model？
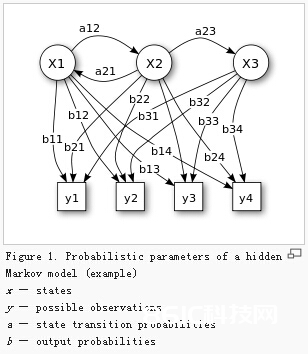
ANS：一个有隐节点（unobservable）和可见节点（visible）的马尔科夫进程（见详解）。
隐节点表明状况，可见节点表明咱们听到的语音或许看到的时序信号。
最开始时，咱们指定这个HMM的结构，练习HMM模型时：给定n个时序信号y1…yT（练习样本）， 用MLE（typically implemented in EM） 估量参数：
1. N个状况的初始概率
2. 状况搬运概率a
3. 输出概率b
————–
在语音处理中，一个word由若干phoneme（音素）组成；
每个HMM对应于一个word或许音素（phoneme）
一个word表明成若干states，每个state表明为一个音素
用HMM需求处理3个问题：
1） Likelihood： 一个HMM生成一串observation序列x的概率 the Forward algorithm>
其间，αt（sj）表明HMM在时间t处于状况j，且observation = {x1，。。.，xt}的概率
，
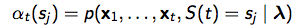aij是状况i到状况j的搬运概率，
bj（xt）表明在状况j的时分生成xt的概率，
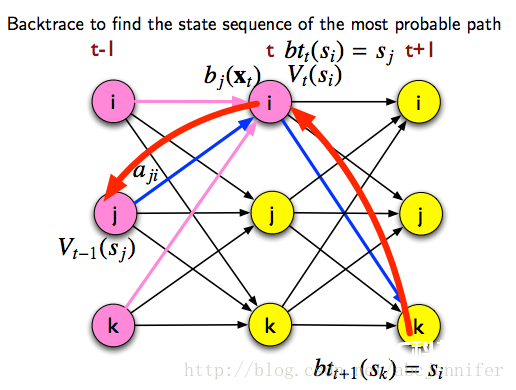
2）Decoding： 给定一串observation序列x，找出最或许隶属的HMM状况序列 the Viterbi algorithm>
在实践核算中会做剪枝，不是核算每个或许state序列的probability，而是用Viterbi approximation：
从时间1：t，只记载搬运概率最大的state和概率。
记Vt（si）为从时间t-1的一切状况搬运到时间t时状况为j的最大概率：
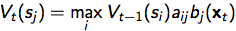
记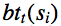
为：从时间t-1的哪个状况搬运到时间t时状况为j的概率最大；
进行Viterbi approximation进程如下：
然后依据记载的最或许搬运状况序列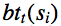进行回溯：
3）Training： 给定一个observation序列x，练习出HMM参数λ = {aij， bij} the EM （Forward-Backward） algorithm
这部分咱们放到“3. GMM+HMM大法处理语音辨认”中和GMM的training一同讲
———————————————————————
GMM是什么？#e#
2. GMM是什么？怎样用GMM求某一音素（phoneme）的概率？
2.1 简略了解混合高斯模型便是几个高斯的叠加…e.g. k=3
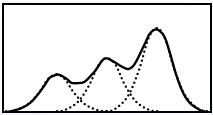
fig2. GMM illustration and the probability of x
2.2 GMM for state sequence
每个state有一个GMM，包括k个高斯模型参数。如”hi“（k=3）：
PS：sil表明silence（静音）
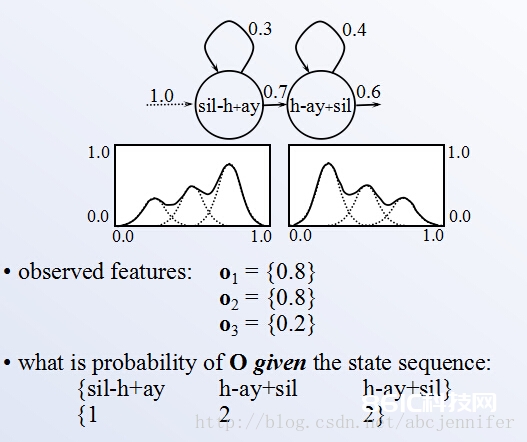
fig3. use GMM to estimate the probability of a state sequence given observation {o1， o2， o3}
其间，每个GMM有一些参数，便是咱们要train的输出概率参数
fig4. parameters of a GMM
怎样求呢？和KMeans相似，假如已知每个点x^n归于某每类 j 的概率p（j|x^n），则能够估量其参数：
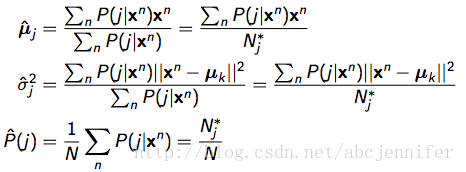
其间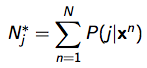 
只需已知了这些参数，咱们就能够在predict（辨认）时在给定input sequence的情况下，核算出一串状况搬运的概率。如上图要核算的state sequence 1->2->2概率：
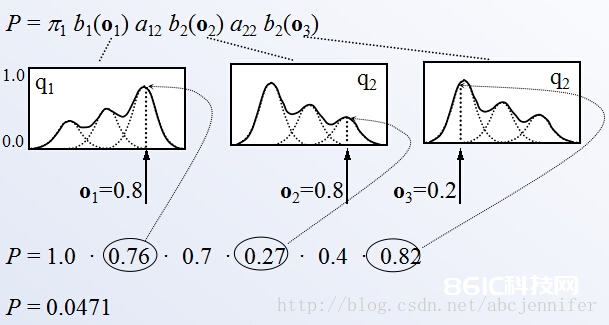
fig5. probability of S1->S2->S3 given o1->o2->o3
———————————————————————
GMM+HMM大法处理语音辨认#e#
3. GMM+HMM大法处理语音辨认
咱们取得observation是语音waveform， 以下是一个词辨认全进程：
1）将waveform切成等长frames，对每个frame提取特征（e.g. MFCC），
2）对每个frame的特征跑GMM，得到每个frame（o_i）归于每个状况的概率b_state（o_i）
fig6. complete process from speech frames to a state sequence
3）依据每个单词的HMM状况搬运概率a核算每个状况sequence生成该frame的概率; 哪个词的HMM 序列跑出来概率最大，就判别这段语音归于该词
宏观图：
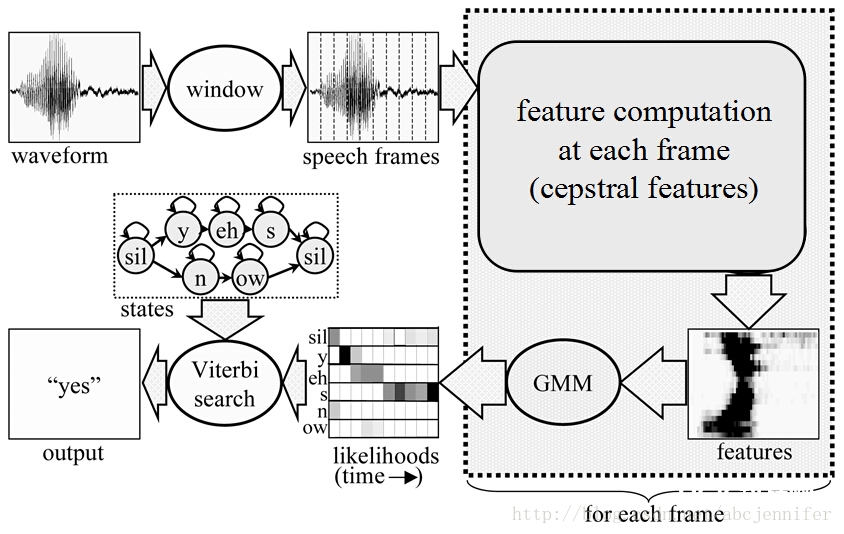
fig7. Speech recognition， a big framework
好了，上面说了怎样做辨认。那么咱们怎样练习这个模型以得到每个GMM的参数和HMM的搬运概率什么的呢？
①Training the params of GMM
GMM参数：高斯散布参数：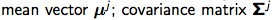
从上面fig4下面的公式咱们现已能够看出来想求参数有必要要知道P（j|x），即，x归于第j个高斯的概率。怎样求捏？
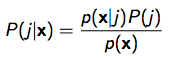
fig8. bayesian formula of P（ j | x ）
依据上图 P（j | x）， 咱们需求求P（x|j）和P（j）去估量P（j|x）。
这儿因为P（x|j）和P（j）都不知道，需求用EM算法迭代估量以最大化P（x） = P（x1）*p（x2）*.。.*P（xn）：
A. 初始化（能够用kmeans）得到P（j）
B. 迭代
E（estimate）-step： 依据当时参数 （means， variances， mixing parameters）估量P（j|x）
M（maximization）-step： 依据当时P（j|x） 核算GMM参数（依据fig4 下面的公式：）
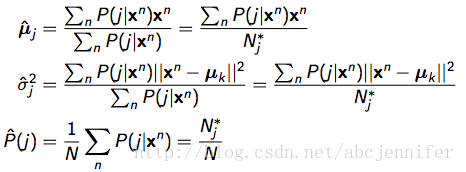
其间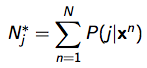
②Training the params of HMM
前面现已有了GMM的training进程。在这一步，咱们的方针是：从observation序列中估量HMM参数λ；
假定状况->observation遵守单核高斯概率散布：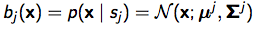
则λ由两部分组成：
HMM练习进程：迭代
E（estimate）-step： 给定observation序列，估量时间t处于状况sj的概率 
M（maximization）-step： 依据从头估量HMM参数aij.
其间，
E-step： 给定observation序列，估量时间t处于状况sj的概率
为了估量， 界说
： t时间处于状况sj的话，t时间未来observation的概率。即
这个能够递归核算：β_t（si）=从状况 si 搬运到其他状况 sj 的概率aij * 状况 i 下观测到x_{t+1}的概率bi（x_{t+1}） * t时间处于状况sj的话{t+1}后observation概率β_{t+1}（sj）
即：
界说方才的为state occupation probability，表明给定observation序列，时间t处于状况sj的概率P（S（t）=sj | X，λ） 。依据贝叶斯公式p（A|B，C） = P（A，B|C）/P（B|C），有：
因为分子p（A，B|C）为
其间，αt（sj）表明HMM在时间t处于状况j，且observation = {x1，。。.，xt}的概率；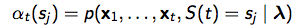
： t时间处于状况sj的话，t时间未来observation的概率；
且
finally， 带入的界说式有：
好，总算搞定！对应上面的E-step方针，只需给定了observation和当时HMM参数 λ，咱们就能够估量了对吧 （*^__^*）
M-step：依据从头估量HMM参数λ：
关于λ中高斯参数部分，和GMM的M-step是相同相同的（只不过这儿写成向量方式）：
关于λ中的状况搬运概率aij， 界说C（Si->Sj）为从状况Si转到Sj的次数，有
实践核算时，界说每一时间的搬运概率
为时间t从si->sj的概率：
那么就有：
把HMM的EM迭代进程和要求的参数写专业点，便是这样的：
