跟着现代电子技能和飞行技能的开展,对雷达的作用间隔、分辩才能、丈量精度和单值性等功能指标提出越来越高的要求,因此雷达信号办法的挑选和信号处理的办法起着重要作用。在脉冲紧缩技能中,雷达所运用的发射信号波形的规划,是决议脉冲紧缩功能的要害。非线性调频信号(NLFM)的频率跟着时刻做非线性改动,NLFM相当于将线性调频信号(LFM)所引进的加权网络的作用搬运分配在发射体系和接纳系
统中,所以无需再用加权网络,而只需改动发射信号的频谱和匹配滤波器的传递函数,因此,NLFM可直接进行匹配滤波即可得到较低的旁瓣而无需加权处理,然后避免了LFM引进加权所带来的信噪比丢失问题。
1 非线性调频信号的规划
NLFM信号的规划首要有两种办法,本文中首要研讨的是窗函数反求法。假定NLFM信号s(t)=a(t)exp[jθt]的频谱为S(ω),对应的匹配滤波器传递函数为S*(ω),则脉压输出信号)y(t)的频谱为
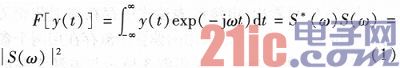
假如挑选某种窗函数W(ω)作为脉压输出信号的频谱,那么也就确认了脉压输出信号,一起确保了脉压输出有足够低的旁瓣电平。
依据停留相位原理有


关于简略的函数是简单求出其反函数的,但关于解析式杂乱的函数来说,求其反函数需凭借数值剖析的办法。
以Hamming窗为例,其函数表达式为这种办法得到的信号调频斜率为S形曲线,因此这种NLFM信号也称作S形NLFM信号。
2 匹配滤波的完结
匹配滤波的完结办法分为频域与时域处理两种办法。时域求解,跟着大时宽的信号匹配时,因为输入离散信号的点数增多,不只硬件资源需求较大,而且需求逐级延时,导致数据添加,核算时刻也会明显添加。频域求解便是将卷积转换为频域的相乘,并运用逆傅里叶改换,将频域相乘的成果再转化时域解。因为本一般运用中时宽带宽积较大,因此需求选用频域办法进行求解,且现在数字逻辑器材处理FFT的速度大幅加速,频域求解法得到广泛的运用。其数学表达式如下
Y(f)=S(f)×H(f) (9)
其间,Y(f)为脉冲紧缩信号的傅里叶改换;S(f)为雷达体系接纳到的信号的傅里叶改换;H(f)为匹配滤波器的傅里叶改换。将Y(f)经傅里叶逆改换,即可得到脉冲紧缩信号y(t),如式(10)所示
y(t)=F-1[Y(f)] (10)
3 仿真验证
规划选用Xilinx FPGA自带的IP核完结FFT算法,该IP核可完结定点复数和浮点复数的FFT改换或IFFT改换,改换长度可到达N=2m,m=3~16,数据精度可到达bx=8~34位,旋转因子精度能够到达bw=8~34位。且在FFT核运转期间,可改动改换长度和每级蝶形运算的切断位数,此IP核有4种完结结构,文中选用定点流水线结构来完结FFT和IFFT。FFT的发动由复位信号操控,因为复数乘法器输出无延时,所以IFFT的发动由FFT的改动完结标志信号(done)操控,完结IFFT的发动。
为节约资源,规划通过Matlab仿真预先得出匹配滤波器的FFT改换成果,存储在ROM中,为确保FFT数据与匹配滤波器系数一起送入复数乘法器,FFT核输出数据索引值(addr)需求加一级寄存器延时之后作为ROM输出数据的地址,输出数据H’(f)送入复数乘法器。FPGA完结框图如图1所示。
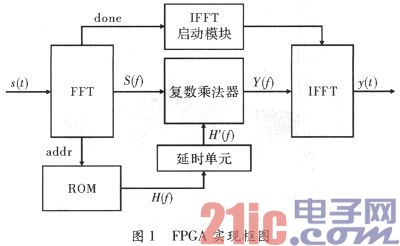
别离规划了一个带宽30 MHz、时长为10.24μs的线性调频回波信号和一个依据Hamming窗的非线性调频回波信号,采样率为100 MHz,输入信号量化位数为16 bit,在FPGA仿真环境下,别离对其进行仿真。
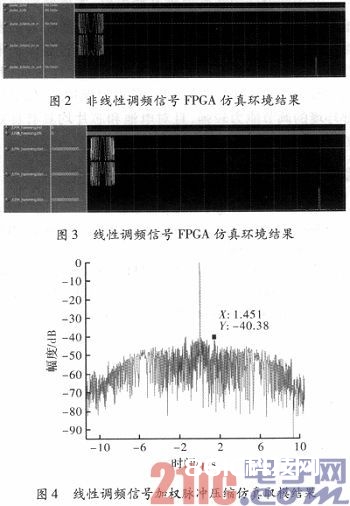
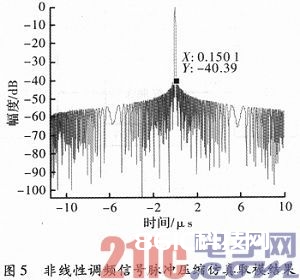
图2和图3别离为非线性调频回波信号和线性调频回波信号在FPGA仿真环境下的仿真成果。因为整个规划均选用流水线结构经行串行处理,所以可满意实时处理的需求,其输入输出数据的延时为74.089μs,将其仿真数据读入到Matlab中对其进行取模比较,在取模后的成果中能够看出,非线性调频回波信号通过脉冲紧缩后主副瓣比可达-40.39 dB。此外,NLFM的脉冲紧缩无需加权处理,然后避免了LFM引进加权所带来的信噪比丢失。
4 结束语
本文运用FPGA仿真环境Modelsim仿真并完结了非线性调频信号的脉冲紧缩算法。选用非线性调频信号无需加权处理即可得到较高的主副瓣比,因此避免了LFM引进加权所带来的信噪比丢失问题。跟着FPGA技能和非线性调频信号规划办法的开展,非线性调频信号的杰出脉冲紧缩作用和FPGA完结的灵活性也将得到广泛运用。