本文介绍一种运用矢量旋转的CORDIC(COordination RotaTIon DIgital Computer)算法完结正交数字混频器中的数控振荡器(NCO)的办法。推导了CORDIC算法发生正余弦信号的完结进程,给出了在FPGA 中规划数控振荡器的顶层电路结构,并依据算法特色在规划中引进流水线结构规划。
在正交数字混频器中,选用数字频率组成技能,能够将数字处理延续到正交调制之后或正交解调之前,滤波器和增益操控就能够用数字办法完结,I、Q两路也就不会存在增益的不平衡,加上数控振荡器(NCO)的低正交差错,能够使体系差错下降到数据的最低比特(LSB)的高精度规模。此外,正交数字混频器更容易与数字信号处理技能结合,使得数字调制愈加灵敏,从而完结软件无线电所要求的软件可更改的调制解调。
数控振荡器是正交数字混频器的中心部分,它具有频率分辨率高、频率改动速度快、相位可接连线性改动和生成的正弦P余弦信号正交特性好等特色。并且NCO的相位、起伏均已数字化,能够直接进行高精度的数字调制解调。跟着数字通信的开展,传送的数据速率越来越高。怎么得到一个可数控的高频载波信号是完结高速数字通信体系有必要处理的问题。为此,对怎么在FPGA中完结高速正交数字混频器中的数控振荡器的办法进行了讨论。
数控振荡器的根本完结原理
数控振荡器的作用是发生正交的正弦和余弦样本。传统办法是选用查表法(LUT),即事前依据各个正余弦波相位核算好相位的正余弦值,并按相位视点作为地址存储该相位的正余弦值,构成一个起伏P相位转化电路(即波形存储器)。在体系时钟的操控下,由相位累加器对输入频率字不断累加,得到以该频率字为步进的数字相位,再经过相位相加模块进行初始相位偏移,得到要输出的当时相位,将该值作为取样地址值送入起伏P相位转化电路,查表取得正余弦信号样本。关于一个相位位数为n ,输出信号起伏位数为M的数控振荡器,所需查找表巨细为M×2n 。为了进步数控振荡器的频率分辨率,往往需求扩展波形存储器的容量,形成存储资源的很多耗费。并且,当需求外挂RAM 来存储波形时,因为遭到RAM读取速度的影响,数控振荡器的输出速率必定遭到约束。因而,当需求规划高速、高精度的数控振荡器时,不宜选用查表法。
为了防止运用大容量存储器,能够考虑运用算法来发生正余弦样本。依据矢量旋转的CORDIC算法正好满意了这一需求,该算法首要用于核算三角函数、双曲函数及其它一些根本函数运算。它有线性的收敛域和序列的特性,只需迭代次数满足,即可确保成果有满足的精度。Walther JS于1971年提出了一致的CORDIC方式。假定初始向量V1(x1 ,y1)旋转视点θ后得到向量V2(x2,y2):
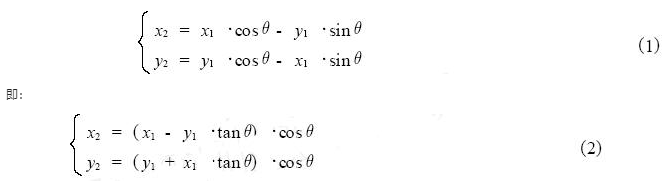
若每次旋转的视点θ是正切值为2 的倍数,即θi=arctan(2-i),则cosθi=(1+2-2i)-1/2 。假定以δi代表矢量的旋转方向,+1表明逆时针旋转,-1表明顺时针旋转,故第i 步旋转可用下式表明:

可见,迭代运算不能使幅值份额因子恒为1。为了抵消因迭代发生的份额因子的影响,可将输入数据X,Y校对后再参加运算,以防止在迭代运算中添加校对运算,下降CORDIC算法的速度。由此运算迭代式能够简化成:
式(5)运算仅经过加法器及移位器就能够完结。此外,若用Zi表明第i次旋转时与方针视点之差,则:

将所需发生的视点值作为z0输入,经过式(5)、(6)的迭代运算,迭代成果输出的xn和yn便是所需求的三角函数值。
数控振荡器的FPGA完结
图1是数控振荡器的顶层电路。由图可见,频率操控字寄存器将接收到的的频率操控字送入相位累加器,相位累加器对体系时钟进行计数,每抵达输入频率操控字的值即对相位进行累加,随后将累加值送入相位相加器,与相位操控字寄存器接收到的初始相位进行相加,得到当时的相位值。其间,相位累加器是决议NCO功用的一个要害模块,能够运用FPGA器材的进位链完结快速、高效的电路结构。可是,因为进位链有必要坐落接近的逻辑阵列块CLB和逻辑单元LC内,所以长的进位链会削减其它逻辑运用的布线资源;一起,过长的进位链也会约束整个体系速度的进步。因而,规划中选用进位链和流水线技能相结合的办法。所谓流水线技能,即把在一个时钟内要完结的逻辑操作分红几步较小的操作,并刺进几个时钟周期来进步体系的数据吞吐率。选用以上做法完结的相位累加器既能确保具有较高的资源运用率,又能大幅进步体系的功用和速度。
经过上述相位的处理之后,即可取得具有所设定初始相位的必定频率的正余弦相位序列,将此序列送入依据CORDIC算法的波形发生器,终究取得两路正交的正余弦输出序列。
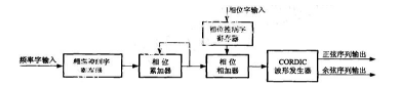
图1 NCO的顶层电路结构
CORDIC迭代算法的一种最直接的完结办法是,只规划一级CORDIC运算迭代单元,然后在体系时钟的驱动下,将本级的输出作为本级的输入,经过同一级迭代完结运算。这种办法尽管很直观,可是为了将核算成果供给给下一级运算而导致占用了很多的寄存器,带来许多额定的资源耗费。而最大的缺陷是运算速度较慢(需求n-1个时钟周期才干输出一个数据),不利于数据的高速实时处理。
因而在实践规划中,选用的是图2所示的由16级CORDIC运算单元组成的流水线结构,正常作业时只需1个时钟周期就能输出1个数据,为数据完结高速实时处理供给了条件。每一级完结的功用是依据式(5)进行一次迭代,移位的位数等于当时的迭代级数,加减法挑选由该级中Z 的最高位(符号位)决议,得到下一级的X 、Y 和Z 的值。经过16级流水线运算后,Z的值变为0,X 和Y 的值则为初始值z0的余弦和正弦值。每一级电路结构首要包含2个移位器和3个加(减)法器,级与级之间直接相连,不需求额定的寄存器。θi 的值为arctan(2-i),可将该小数转化为二进制数后,存储于存储单元中,为每一级流水线供给查找表。若关于16级的流水线结构,则的规模是0~15。
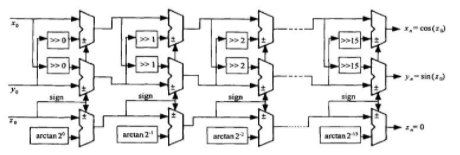
图2 CORDIC迭代算法的流水线结构
规划中还应该留意迭代序列所能掩盖的视点规模,若直接选用n 级迭代序列:0 ,1 ,2 ,…,n – 1 ,则迭代所能掩盖的视点规模仅有- 99.9°~99.9°。本规划选用了添加迭代次数的办法来扩展视点掩盖规模,即添加两个i = 0 的迭代,将迭代序列扩展为0,0,0,1,2,…,n-1,从而使视点掩盖规模也扩展到-π~π。
数控振荡器的仿真成果及功用剖析
运用Altera公司的QuartusII软件,选用VHDL硬件描绘言语对上述数控振荡器结构进行描绘,在Modlesim上经过功用仿真,成果正确后综合出电路网表,最终将程序下载至Altera公司出产的StraTIx器材EP1S20B780C6完结。
因为规划中选用了StraTIx器材,该器材的32位加减器作业频率能够到达90MHz以上,为发生高速的正交信号供给高速牢靠的的作业时钟。考虑到NCO的作业时钟瓶颈是在相位累加器,因而能够依据详细需求减缩相位累加器的位数来进步NCO的作业时钟。本文规划的NCO作业时钟为100MHz,相位累加器的位数为16位,输入的频率操控字为4CCCH,依据公式:
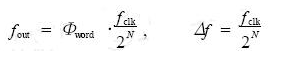
其间:Φword为输入的频率操控字;fclk为作业时钟;N为相位累加器位数,可算出NCO输出的正余弦信号的频率;fout为30MHz ;频率分辨率Δf ≈1.5 kHz。频率分辨率说明晰若经过输入频率操控字来改动输出正余弦信号的频率时,能够到达1.5 kHz 的最小步进。别的,也能够依据实践需求的频率改动输入频率操控字值。当然,NCO输出频率的上限要遭到Nyquist规律的约束,即fout的最大值为fclkP2,实践规划一般不大于0.4fclk。图3为数控振荡器的部分仿真时序图。

图3 NCO的部分仿真时序图
结语
研讨了正交数字混频器中数控振荡器的规划与完结办法,侧重剖析了怎么在FPGA器材中运用CORDIC迭代算法发生正余弦信号。成果表明,依据CORDIC迭代算法的数控振荡器,仅用移位寄存器和加法器就可发生正余弦信号,不光省去了传统NCO巨大的存储器资源,并且保留了一般数控振荡器频率分辨率高、频率改动速度快、相位可接连线性改动、生成的正弦P余弦信号正交特性好等特色,十分适用于在正交数字混频器中进行高速高精度的数字调制解调。
责任编辑:gt









