在追求高精度测量的时代,光学系统的像差校正显得至关重要。通过理论分析、基于奇异值分解的像差校正和暗场数字全息显微术的实验研究,本文深入探讨了如何提高半导体测量的精度和效率。
理论分析
理论部分深入分析了光学系统的分辨率和镜头设计对成像质量的影响。特别介绍了非等面像差的性质及其对成像准确性的影响。通过理论模型和分析,探索了如何在设计和构建光学系统时最大限度地减少这些像差。解释了瞳孔畸变对成像的影响,以及如何通过调整光学系统来减少这种畸变。这些讨论为实验部分中使用的暗场数字全息显微术提供了必要的理论基础,以提高半导体测量的精度和效率。

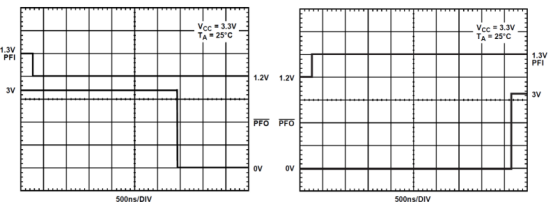
图1:球面波照射成像透镜的点扩散函数(PSF)以及理想球面波前的PSF和非理想球面波的PSF
基于奇异值分解的像差校正
如何利用奇异值分解来校正像差,奇异值分解(SVD)校正像差的过程涉及使用SVD算法来分析和调整成像系统的数据,以减少或消除非等距像差。SVD能够从成像数据中提取关键信息,并通过数学处理分离出图像中的误差成分。这种方法特别适用于处理复杂的像差,如非等距像差,它们在传统的像差校正方法中难以解决。通过SVD,可以优化图像质量,提高半导体计量中的精度和效率。
暗场数字全息显微术
接下来详细描述了暗场数字全息显微术的实验设置,包括光学系统的配置、数据采集过程和数据处理方法。重点放在了如何使用特定的光学技术和计算算法来校正非等面像差,特别是如何利用SVD技术校正非等面像差。以提高半导体计量的精度。这部分还包括了对实验结果的校验方法,确保所得数据的准确性和可靠性。
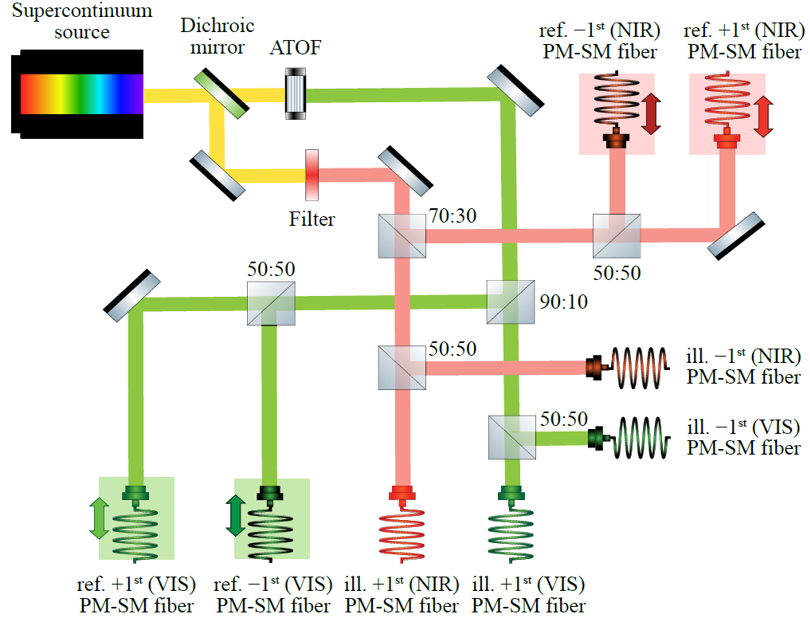
图2:实验装置示意图
实验结果
在实验结果部分,首先展示了使用特定校准样本进行四维PSF校准的过程及其结果。接着,展示了针对特定覆盖目标图像的非等面像差校正结果。实验结果证明了非等面像差校正方法在暗场数字全息显微术中的应用能够有效提高半导体计量的精度和成像质量。
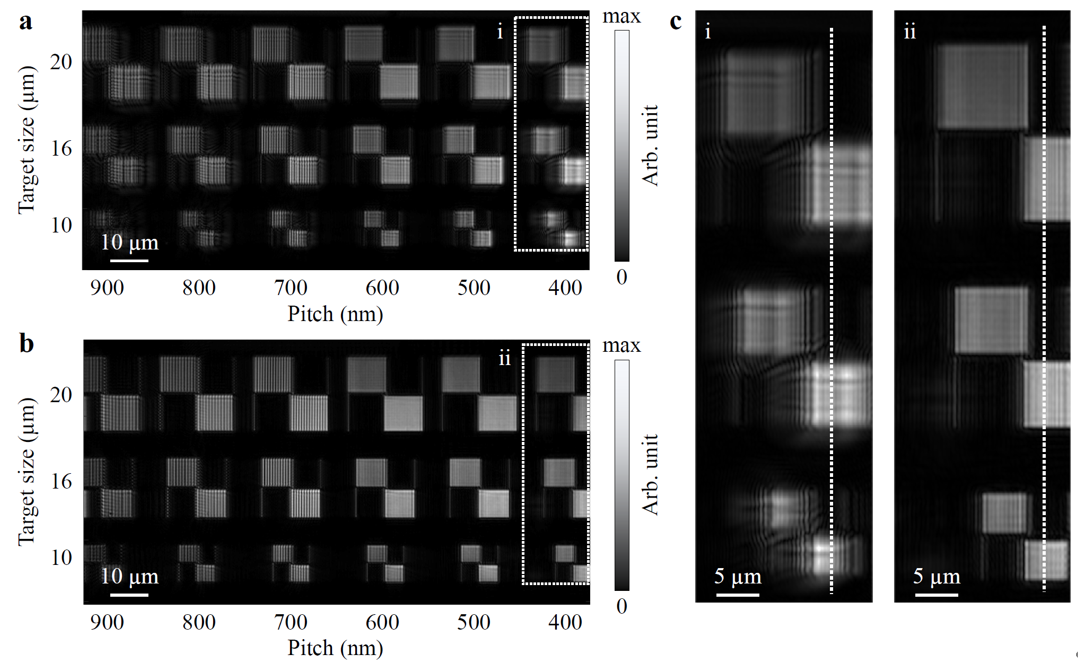
图3:可见光波段像差校正的实验结果