作者 吴漾 朱州 贵州电网有限责任公司信息中心(贵州 贵阳 550003)
吴漾(1984-)，男，硕士，工程师，研讨方向：电网信息化数据办理与数据剖析办理;朱州，男，高级工程师，博士，研讨方向：电网信息化建造与数据剖析办理。
摘要：本文从电力欠费危险猜测的视点动身，提出了一种依据特征挑选改善的LR-Bagging(即以逻辑回归为基分类器的Bagging集成学习)算法，其精华在于每一个练习的LR基分类器的记载和字段均经过随机抽样得到。且算法的中止迭代准则由AUC计算量的改动率决议。该改善算法充分考虑了LR的强泛化才能、Bagging的高准确度，以及特征挑选带来的LR基分类器的多样性、弱化的多重共线性与“过拟合”度，作用优于单一LR模型。且终究的试验标明，该改善算法得到的电力欠费居民客户危险猜测模型的准确性与有用性得到进步。
导言
我国电力体系的深化改革为电力职业引入了商场机制[1]，在有用完成电力资源优化装备，进步电力资源出产和传输功率的一起，也带给电力企业更大的商场危险，危险的实在防备和躲避对电力企业的重要性显而易见。因为客户欠费而发生的电费收回危险一直是电力营销中存在的严重危险之一。
首要，国内学术界专业人士关于该问题的研讨起步较晚[3]，首要集中于对电费收回危险的现状、影响要素、点评、有用性办法等内容的理论研讨，缺少以实际数据为根底量化模型支撑[3-4];尽管也有许多文献经过对电力客户信用等级建模对其欠费危险进行猜测[5]，但模型不行直接;跟着大数据发掘职业的蓬勃发展，近几年呈现了依据逻辑回归、决议计划树的数据发掘算法的电力客户欠费违约概率猜测模型[6-7]，但前者选取特征均为二分类变量，适用性较低;后者挑选的模型变量虽较为多样性，但模型的猜测成果差强人意。而本文将凭借电力客户属性数据和行为特征数据，尽或许发掘每一个变量与欠费危险的相关信息，树立一个更为准确、运用规模更广的客户欠费危险猜测模型。
其次，现在关于LR的文章或许关于Bagging集成学习的文章有许多，可是依据LR分类器的Bagging算法的运用相对较少，经过特征挑选对依据LR分类器Bagging算法做出改善的相关文献根本没有。简略来说，本文算法为多个不同的LR分类器的调集，其间心在于每一个练习的LR基分类器的样本和特征均经过bootstrap技能得到。充分考虑了LR的强泛化才能、Bagging的高准确度，以及特征挑选带来的LR基分类器的多样性，使得该算法在精度、实用性上优于单一算法，后文的运用刚好证明了这一点。鉴于该算法的这一优越性，可测验将其运用于其他范畴的分类发掘问题。
本研讨的含义体现在两个方面：一是关于电力欠费客户危险猜测这一模块的进一步研讨;二是依据特征挑选的以LR为基分类器的Bagging算法的改善的学习和推行价值。
1 依据LR分类器的Bagging算法的改善
1.1 LR模型及其根本理论
逻辑回归(LogisticRegression，LR)模型是一种分类鉴定模型，是离散挑选法模型之一。它首要是用于对受多要素影响的定性变量的概率猜测，并依据猜测的概率对方针变量进行分类。逻辑回归可分为二项逻辑回归和多项逻辑回归，类别的差异取决于方针变量类别个数的多少。现在，LR模型现已广泛运用于社会学、生物计算学、临床、数量心理学、商场营销等计算实证剖析中，且以方针变量为二分类变量为主。
1.1.1 Logistic函数
假定因变量只要1-0(例如“是”和“否”，“发生”和“不发生”)两种取值，记为1和0。假定在p个独立自变量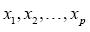
作用下，y取1的概率是
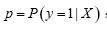，取0的概率是1-P，则取1和取0的概率之比为
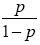，称为事情的优势比(odds)，表明事情发生的概率相关于不发生的概率的强度。对odds取自然对数可得Logistic函数为：
(1)
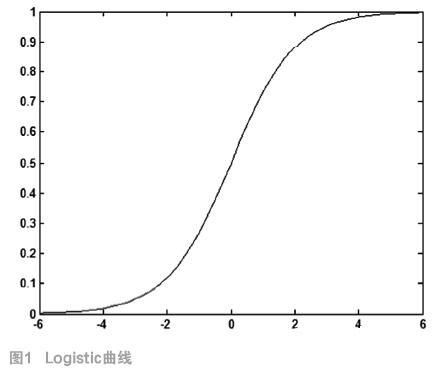
Logistic函数曲线如图1所示。
1.1.2 LR模型
LR模型能够探求因为自变量的改动所能导致的因变量决议计划(挑选)的改动，因变量决议计划(挑选)的改动意味着Logistic函数的改动。LR的根本方式为：
因而有：
1.1.4 LR模型的优势与缺乏
LR模型具有很强的实用性，比照其他的分类判别模型，LR具有以下两点优势：
(1)泛化才能较好，精度较高
所谓泛化才能，是指机器学习算法对新鲜样本的适应才能。因为LR模型的自变量多为取值规模不设限的连续变量，该模型不只能够在样本内进行猜测，还能够对样本外的数据进行猜测，泛化才能较好，并且精度较高。
(2)能准确操控阈值，调整分类类别
LR模型的求解成果是一个介于0和1间的概率值。这使分类成果的多样性成为了或许。正常情况下，每一次阈值的调整都会发生不同的分类成果，便于对猜测成果进行比较和查验，克服了其他分类算法分类数量无法改动的限制。
当然，LR作为回归模型的特别方式，也需求满意经典回归模型的根本假定，违反这些假定显然会影响模型的分类作用，多重共线问题便是现在面对较多的问题。一起，逻辑回归的功能受特征空间的影响很大，也不能很好地处理很多多类特征或变量，这便是LR分类器的缺陷地点。
2 Bagging集成学习
2.1 集成学习
集成学习[8]是一种机器学习范式，它的根本思想是把多个学习器(一般是同质的)集成起来，运用多个模型(处理方案)来处理同一个问题。因其个别学习器的高精度和个差错均散布于不同的输入空间，从而能到达显著地进步学习体系的泛化才能的作用。
Breiman一起指出，要使得Bagging有用，根本学习器的学习算法有必要是不稳定的，也便是说对练习数据灵敏，且根本分类器的学习算法对练习数据越灵敏，Bagging的作用越好。别的因为Bagging算法自身的特色，使得Bagging算法十分合适用来并行练习多个根本分类器，这也是Bagging算法的一大优势[8]。
2.3 本文算法描绘
前文指出，一方面，学习器的稳定性，即对练习数据的灵敏性，很大程度上影响Bagging算法的作用，其间原因在于差异性小的数据对稳定性较强的学习器无法很好发生作用，这将影响到基学习模型的多样性，Bagging算法进步准确度的才能也将大大削弱，而LR模型的不稳定功能不杰出;另一方面，LR对大特征空间的解说作用并不抱负，且越多的变量特征也将加大变量间多重共线的或许性，LR模型的显著性无法得到保证。
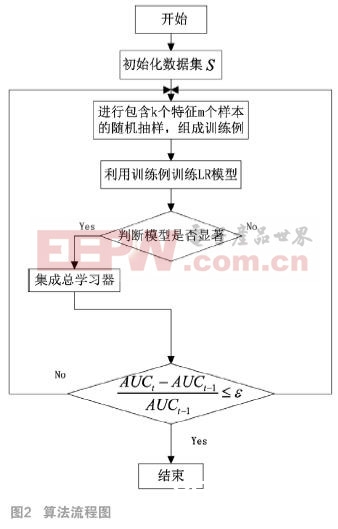
因为上述两点原因，本文提出了一种依据特征挑选的LR-Bagging(基分类器为LR的Bagging算法)的改善算法。该算法的精华在于对每一个LR进行练习的特征变量需求经过有放回的随机抽样发生。如此改善的意图在于经过削减或改动变量进步基LR分类器的多样性，削减变量间的多重共线性与过拟合问题，一起还能较好保存LR与Bagging集成学习的长处。
AUC(Area Under Curve)被界说为ROC曲线下的面积，它的取值规模介于0.5到1之间，是比较分类器间分类作用好坏的点评规范。AUC越大，咱们以为模型的分类作用越好。一般情况下，，跟着循环次数的添加，模型提取的数据信息量也会不断添加，最终到达峰值，所以咱们一般能够以为组合模型的作用趋于先不断加强后保持稳定的进程。因而，咱们把迭代的中止条件的设置为是合理的。
