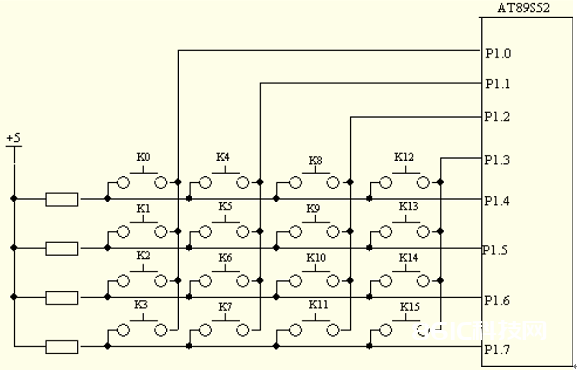
在单片机按键使用进程中,当键盘中按键数量较多时 为了削减端口的占用一般将按键排列成矩阵 方式如下图所示,在矩阵式键盘中 每条水平线和垂直线在交叉处不直接连通而是经过一个按键加以衔接,究竟这样做是出意何种意图呢? 咱们看下面电路图,单片机的整一个8位端口能够构成 4*4=16 个矩阵式按键 ,比较独立式按键接法多出了一倍,并且线数越多差异就越显着,假设再多加一条线就能够构成 20个按键的键盘,可是独立式按键接法只能多出1个按键。由此可见,在需求的按键数量比较多时,选用矩阵法来衔接键盘是十分合理的,矩阵式结构的键盘明显比独立式键盘杂乱一些,单片机对其进行辨认也要杂乱一些。承认矩阵式键盘上任何一个键被按下一般选用行扫描法。行扫描法又称为逐行查询法它是一种最常用的多按键辨认办法。因而,咱们就以行扫描法为例介绍矩阵式键盘的作业原理。
图5-4(4*4矩阵式按键的接法)
首要,不断循环地给低四位独立的低电平,然后判别键盘中有无键按下。将低位中其间一列线(P1.0~P1.3中其间一列)置低电平然后检测行线的状况(高4位,即P1.4~P1.7,因为线与联系,只需与低电平列线接通,即跳变成低电平),只需有一行的电平为低就延时一段时间以消除颤动,然后再次判别,假设仍然为低电平,则表明键盘中真的有键被按下并且闭合的键坐落低电平的4个按键之中任其一,若一切行线均为高电平则表明键盘中无键按下。再其次,判别闭合键地点的详细位置。在承认有键按下后 ,即可进入承认详细闭合键的进程。其办法是: 顺次将列线置为低电平,即在置某一根列线为低电平时,其它列线为高电平。一起再逐行检测各行线的电平状况 ;若某行为低 ,则该行线与置为低电平的列线交叉处的按键便是闭合的按键。下面图5-5是4*4矩阵式按键接法的软件算法操作流程。
下面程序依照上述算法流程去编写的,其电路如图5-6,只是在图5-5的基础上多加了P0端口的8只LED灯。从键盘中检测到一个键值,然后将这个值写到LED数码管上显现。
#include
#include
#define uchar unsigned char
#define uint unsigned int
uchar temp,num;
uchar code Dis_code[]={0xc0,0xf9,0xa4,0xb0,0x99,0x92,0x82,0xf8,0x80,0x90, 0x88,0x83,0xc6,0xa1,0x86,0x8e,0xff}
//0,1,2,3,4,5,6,7,8,9,a,b,c,d,e,f,0ff
void delay(uchar ms)
{
int i;
while(ms–)
{
for(i=0;i<100;i++) ;
}
}
uchar keyscan()
{
P1=0xfe;
temp=P1;
while(temp!=0xfe)
{
temp=P1;
switch(temp)
{
case 0xee:num=1;
break;
case 0xde:num=2;
break;
case 0xbe:num=3;
break;
case 0x7e:num=4;
break;
}
delay(100);
}
P1=0xfd;
temp=P1;
while(temp!=0xfd)
{
temp=P1;
switch(temp)
{
case 0xed:num=5;
break;
case 0xdd:num=6;
break;
case 0xbd:num=7;
break;
case 0x7d:num=8;
break;
}
delay(100);
}
P1=0xfb;
temp=P1;
while(temp!=0xfb)
{
temp=P1;
switch(temp)
{
case 0xeb:num=9;
break;
case 0xdb:num=10;
break;
case 0xbb:num=11;
break;
case 0x7b:num=12;
break;
}
delay(100);
}
P1=0xf7;
temp=P1;
while(temp!=0xf7)
{
temp=P1;
switch(temp)
{
case 0xe7:num=13;
break;
case 0xd7:num=14;
break;
case 0xb7:num=15;
break;
case 0x77:num=16;
break;
}
delay(100);
}
return num;
}
void Display(uchar Wei_8,uchar Wei_7,uchar Wei_6,uchar Wei_5,uchar Wei_4,uchar Wei_3,uchar Wei_2,uchar Wei_1)
{
P2=0xfe;
P0=Dis_code[Wei_8];
delay(1);
P2=0xfd;
P0=Dis_code[Wei_7];
delay(1);
P2=0xfb;
P0=Dis_code[Wei_6];
delay(1);
P2=0xf7;
P0=Dis_code[Wei_5];
delay(1);
P2=0xef;
P0=Dis_code[Wei_4];
delay(1);
P2=0xdf;
P0=Dis_code[Wei_3];
delay(1);
P2=0xbf;
P0=Dis_code[Wei_2];
delay(1);
P2=0x7f;
P0=Dis_code[Wei_1];
delay(1);
}
void main()
{
while(1)
{
Display(keyscan(),16,16,16,16,16,16,16)
}
}