耦合腔行波管具有作业带宽适中，高功率，高功率，高增益和杰出的散热才能的特性，因而被广泛地应用于卫星通信、雷达、遥感遥测等范畴。现在在研发行波管时遍及选用三维PIC粒子模仿软件辅导规划，国内外不少文献都有相关报导。在此选用形式展开法建立了考虑相对论效应时耦合腔行波管一维非线性注一波互效果作业方程组，选用田炳耕的圆盘模型核算了空间电荷场，并对互效果作业方程组进行数值求解，剖析一个作业在S波段的休斯结构耦合腔行波管的一些重要的非线性特性如功率、增益、带宽。评论了空间电荷场对注一波互效果的影响。
1 根本方程
1．1 激起方程
令第n次本征形式轴向电场为：
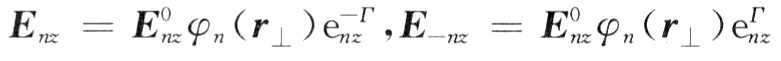
可得扰动电子注鼓励的电场为：
式中：界说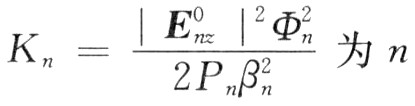
为n次谐波的耦合阻抗；
ψ(r⊥)为电子注横向散布函数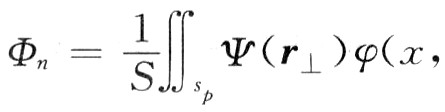
y）ds。一切本征模中只要单个形式与电子注同步，且除了电子流i（z）激起的同步波之外，还有输入的“冷波”，即E0e-r0z，则具有外加鼓励源E0e-r0z的同步场为：
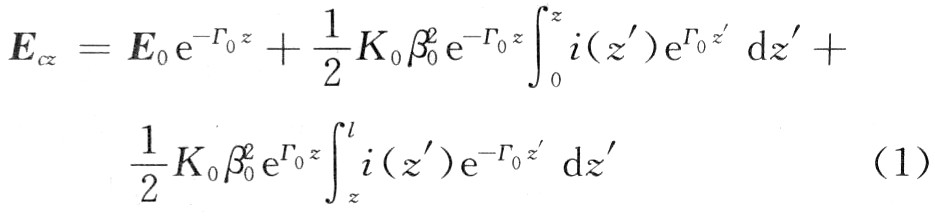
式中：K0，г0，β0分别为该同步形式的耦合阻抗、传播常数、相位常数。式(1)两头一起对z求导2次得到熟知的激起方程：
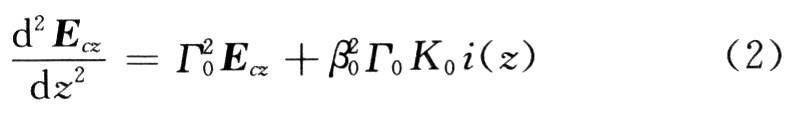
1．2 运动方程
相对论下电子的运动方程为：
能量守恒方程为：
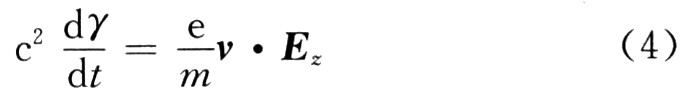
式(4)代入式(3)可得一维电子运动方程：
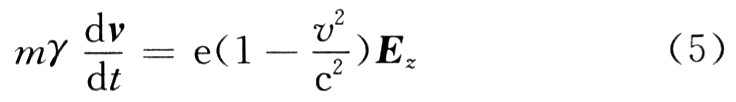
又由：
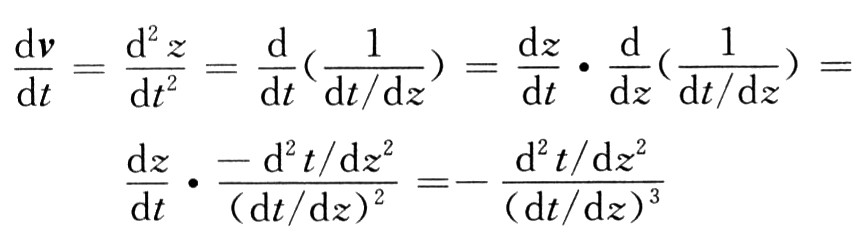
所以式(5)可写为：
其间：Ez=Ecz(线路场)+Esz(空间电荷场)；y=(1一v2/c2)-1/2为相对论因子，c为真空中的光速，v为电子速度。
1．3 电子流复振幅方程
电子流是时刻的非简谐周期函数，含有高次谐波，用傅氏剖析。
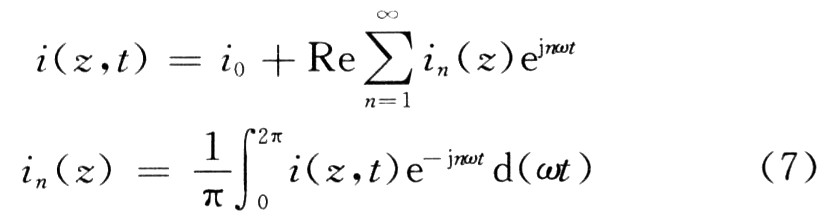
2 慢变体系中归一化
上述是在试验室坐标系下得到的迅变方程，为了处理问题的便利和核算成果遍及性强，一般将其归一化到电子坐标系内，取得慢变方程。
为了表述便利，先引进迅变坐标系的归一化量：归一化间隔为ξ=ω/v0z=βez；归一化时刻为φ=ωt=2πt=/T，归一化场为f=|e|E/mvoω。则慢变体系中的归一化：归一化轴向间隔为θ=Cξ=Cβez；归一化相位φe=ψ-ξ；归一化场幅值为Fcn(θ)=(eE／C2mvoω)ejnθ；归一化电流幅值为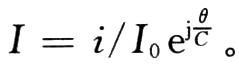
式(8)～(10)组成了行波管大信号注一波互效果根本作业方程组。其间Cn3=I0Kcn/4V0为n次谐波增益参量，bn=(V0一Vpn)／C1Vpn非同步参量，dn=aon／βeCn为衰减常数，rn=bn-idn。
3 空间电荷场的核算
由文献可知z0处圆盘在z处圆盘平面上各点发生的均匀空间电荷场为：
其间：Q为圆盘所带电量；6为电子注半径；a为漂移管半径，如图1所示，μ0n为零阶Bessel函数的第n个根。由此可知场是关于z的函数，能够表明为：
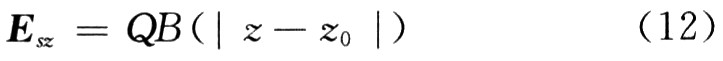
其间：B(| z―z0|)是以| z―z0|为变量的函数，由式(11)能够做出如图1所示曲线。
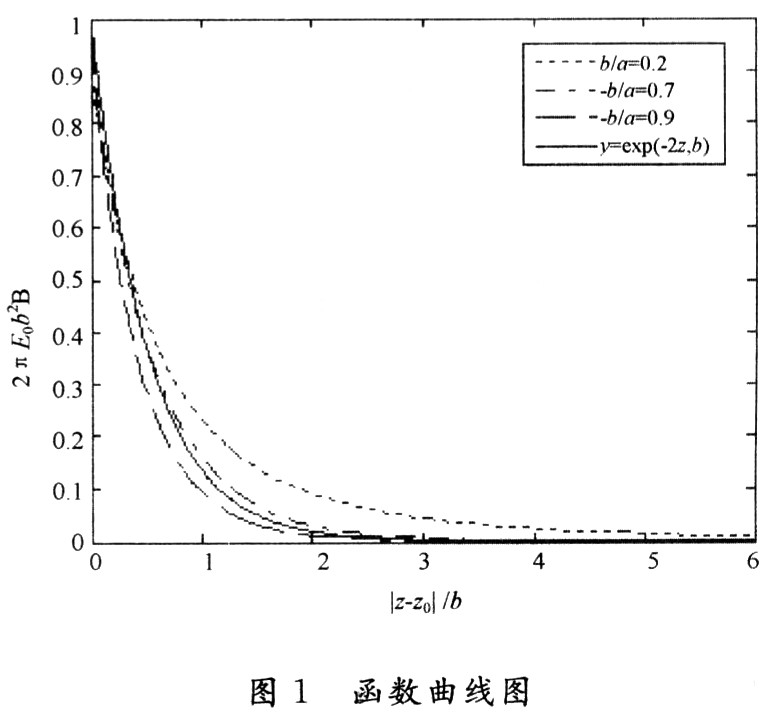
由图1可知，假如用近似式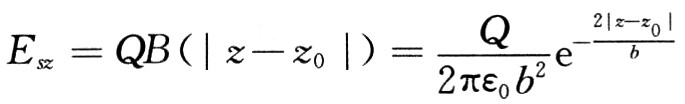
替代式(11)，所引起的差错很小，而核算式却大大简化了。选用该式时，一切圆盘发生的空间电
，
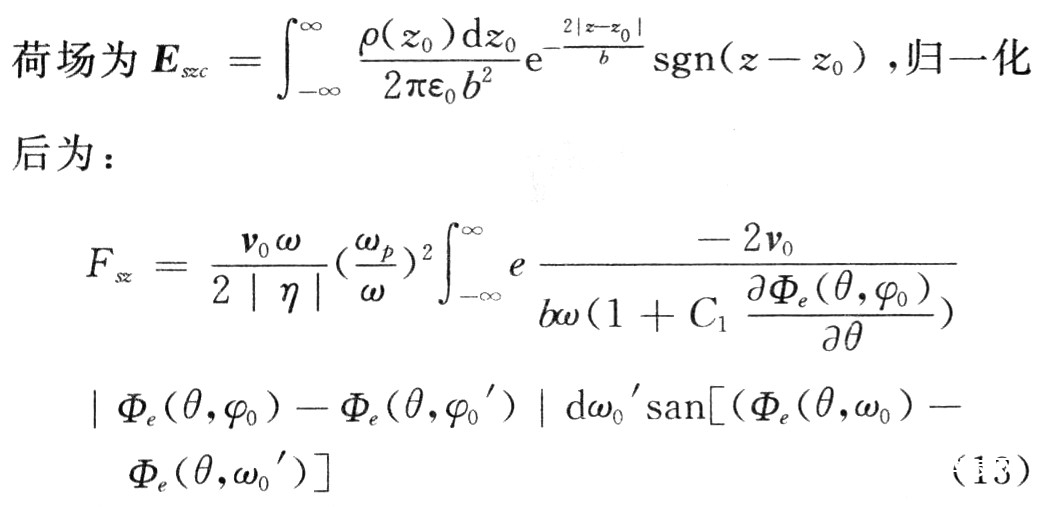其间：ωp为电子等离子体频率；η为电子荷质比；v0为电子注初速度。仿真顶用式(13)替代式(9)中的Fsz。
4 休斯结构耦合腔
休斯型耦合腔的剖面结构为图2(a)所示，图2(b)为其截面图，表1为规划s波段耦合腔行波管的结构参数。
5 仿真成果及评论
在上述尺度下，对2．87～3．35 GHz频率范围内的休斯结构耦合腔行波管进行了数值剖析，仿真中电子注的注电压U。一21 kV，注电流L一1 A，波的输入功率Pin=300 w。选用四阶龙格一库塔法求解互效果方程组式(8)～(10)，其成果如图3～图6所示。
图3给出了在中心频率f=3．100 7 GHz时电子的相位轨道。由图可知，电子在归一化轴向间隔Z=2．4邻近取得了较好的群聚，此即为最佳互效果间隔。由图4能够看出该频率的波在此处取得最大增益，尔后电子注脱离最佳互效果区，功率下降，增益下降。
图5给出了中心频率时电子注功率随轴向间隔的改变曲线。图中实线为不考虑空间电荷力的状况，虚线为考虑空间电荷力的状况。由图可知，空间电荷力的效果使得饱满方位推后，增益下降，即空间电荷力起发散效果。图中功率刚开始时为负值，是因为电子刚进入互效果区时要得到部分能量，体现电子功率为负值。
图6给出考虑空间电荷场时，2．87～3．35 GHz内各频点的微波增益。由图可知，在给定电子注注电压，注电流，和波的输入功率等参量的状况下，频带内微波增益均大于18．5 dB。
6 结 语
对S波段休斯结构耦合腔行波管非线性注一波互效果作业方程组进行了数值求解，求出考虑和不考虑空间电荷场时中心频率．厂一3．100 7 GHz处的功率，阐明空间电荷场对互效果起散焦效果，与文献中定论很符合。求出作业在2．87～3．35 GHz频率范围内耦合腔行波瞬时带宽。仿真中所用管子已制造完结，试验数据对后期管子的热测验有很好的辅导意义。
