导言
本文以飞思卡尔智能车大赛为布景，运用飞思卡尔(Freeseale)出产的16位微操控器MC9S12XS128作为操控中心，制造一个能巡线快速行进的摄像头小车。因为摄像头光轴与地面呈必定夹角，所以其成像存在梯形失真;为了扩展视界，广角镜头越来越为许多部队所选用，所以又存在桶形失真。这两种失真，是每个选用广角镜头的摄像头部队都要遇到的问题。许多部队都逃避这个问题，直接选用图画预处理后的像素点进行操控。但若将像素点转化为实践物理坐标，无疑更直观，对程序的编写或建模带来很大的便利，并且本文提出的这个办法，可有用处理这两种失真，实践操作并不杂乱。
各队处理计划总述
文献[1]提出的办法是：能够经过关于每行提取的路途方位经过一个线性修正来消除梯形失真，可经过试验的办法确认线性补偿的系数。可是该试验办法比较冗杂，并且不能消除桶形失真。
文献[2]制造了一个图画标定板，如图1所示。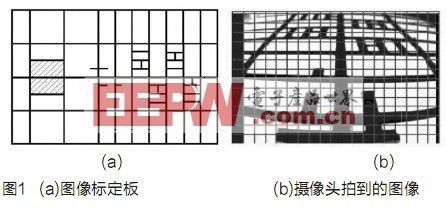
其原理是：图1(a)中暗影部分是车体放置的方位。在标定板上等间隔地贴了许多黑线，给标定板摄影后，就能够知道实践中的方位与图画中的方位的相互联系。这个办法因为黑线有必定宽度，所以会存在较大差错。
文献[3]选用非均行收集的计划。所谓非均行收集是与均行收集对应的。在均行收会集，AD模块所收集的行均匀散布于摄像头输出的图画中。而非均行收集则是指，AD模块所收集的行按某种规矩非均匀地散布在原始图画中，而这种规矩是确保收集得到的图画在纵向上(小车中轴方向)与实践景象不畸变。然后再确认每一行的横向畸变系数。
如图2所示，非均行收集时，远处采得密，近处采得稀。因为摄像头装置办法在试验时会常常变化，以确认最佳俯角和最佳高度，每逢变化就需求从头标定。这个计划就不大便利了。文献[4]树立了一个光路几许模型图，如图3所示。
试验计划：量取摄像头架固定螺钉的高度H与摄像头中心相关于竖直杆的偏转视点(俯角)θ。因为光学中心的核算完全由这两个数据及近端距固定杆的间隔S(即丈量保险杠距固定杆的间隔S0和近端距保险杠间隔S’相加得到，也可直接在试验板上丈量由近端黑线到摄像头固定杆的间隔S)确认，因而要做到越精确越好。由O点做垂线长度为H至点A，做水平线AB，截取AD长为S，DB过O点做与笔直线成θ的射线交AB于C，过D做DE笔直于OC，并使OC为DE的笔直平分线，衔接BE并延伸，交OC与O’，则O’为光学中心。从图上能算得O’距底边间隔为H’，俯角不变。
将试验板笔直放置，做出边长为A1的正方形标定区域，即图3中的DE平面，将摄像头水平对向试验板中心C，摄像头架固定螺钉距试验板间隔为H1。读出标定试验板上特征点的相应像素点。能够得到图4中(X，Y)与像素点(U，V)的联系(U为行数，V为列数)。
因为试验平面与实在视界平面之间是纯几许联系，因而这部分转化函数联系能够用几许推导。 其公式较杂乱，在这儿纷歧一列出。
其公式最大的坏处在于有许多sin()、cos()等三角函数运算，但单片机做这种运算会花费很多时刻，所以本应尽量防止呈现三角函数、开方等运算。并且，若选用广角镜头或摄像头架得较低时，B点将会距A点很远而找不到B点。所以该办法也不具通用性。试验自身也比较杂乱。
文献[5]选用的试验办法是：事先在一块白板上画一系列小的正方格，正方格越小，精度越高。然后标定中心黑粗线，用来确认赛车的摆放方位和图画的中心。如图5所示。之后能够直接读出各特征点相应的像素坐标，树立对应联系。
该试验计划很直观，但其操作未必简洁。因为摄像头视界较广，所需纠正网络也较大，在其上画方格线很难确保肯定水平或笔直。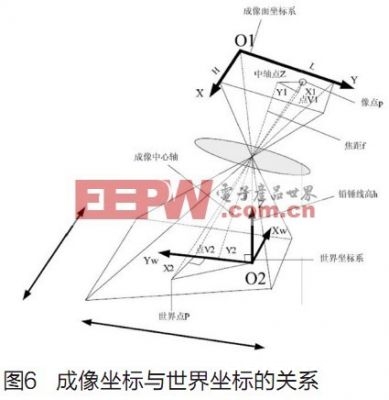
文献[6]依据几许数学建模，得出摄像头获取图画的成像坐标与景象实践的国际坐标的联系。
坐标改换联系如下：
在摄像头装置固定后，c/tanθ、a、b、c、h 和h/cosθ 均为常量。这个办法仍是比较好的，可是需求知道f、L、H，这三个参数厂家会供给，但不必定精确，θ也较难精确丈量，且不能处理桶形失真的问题。
几许失真校对办法
建模剖析
如图7所示，国际坐标系中的点P(Xw，Yw，Zw)首要经过刚体改换到摄像头坐标系中的点P(X，Y，Z)。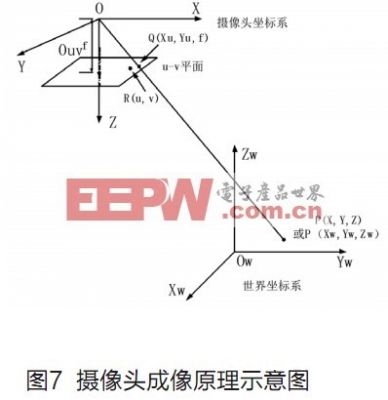
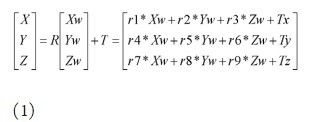
然后再从摄像头坐标系到抱负的图画坐标系的透视改换。
图8是一镜头抱负成像原理图，图中左面的直线是方针，右边的直线是方针所成的象。从图中能够看出，方针中心点O点成象于象的中心O′点，方针上不同的两点A点和B点成象于A′和B′点，且有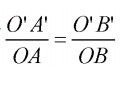
。但大视场角使得广角镜头不能再等效为抱负透镜，而是一个焦距跟着方针离光轴间隔增大而减小的成象体系。依据牛顿成象定理，方针高度r与对应象高r′之间的核算联系为
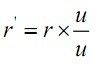。在物距m必定的状况下，焦距f愈小，象高r′愈小。这样，跟着方针离光轴间隔r的添加，焦距f跟着减小，所成图象就产生了桶形失真。由以上的剖析可看出，桶形失真能够当作像素点向心径向缩短，且跟着方针距光轴间隔r的添加，缩短率增大。因而，假如使失真图象中的像素离心径向按不同膨胀率增大，即可完成几许失真校对。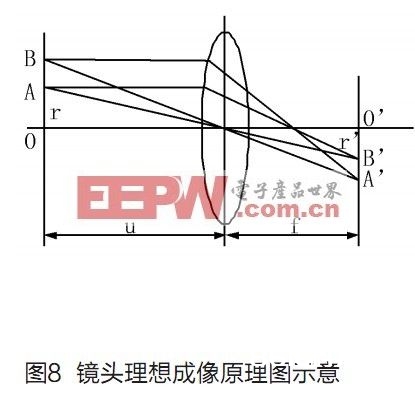
试验办法
状况(1)：摄像头俯角小，虽有桶形失真，但要害区域处于图画中部。如图9所示。分段逆透视改换适用于这种状况。
若疏忽桶形失真，即让U=Xu+Center_u，V=Yu +Center_v(注目的7中图画原点Ouv在摄像头坐标系中坐标为(- Center_u，- Center_v，f))，则由公式1和公式2可知，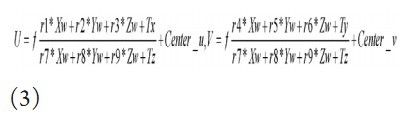
因为Zw=0，上式又可写成: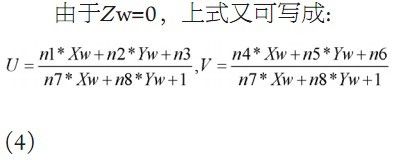
反解Xw，Yw，可得: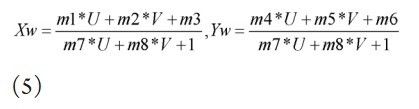
上式又可写成: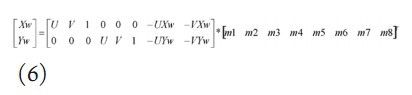
理论上依据4个点m1-m8就能够有一组解。
试验过程如下：以车头为原点，在车头前选取8个点，如图10所示(单位：cm)。 选点要求规模尽量大，跑道常常呈现的区域，但又不能处于摄像头输出图画边际区域;从图9中读出各点像素坐标(a，b);依据分辨率将各像素坐标转化为单片机图画坐标，这是一个线性改换;将8个点分红near、middle、far三组，每组4个点，依据式6可求出三组解。
在单片机程序中，当图画预处理得到(U，V)后，可依据式5解出(Xw，Yw)，差别是(U，V)处于不同方位时用不同的参数。因为相邻梯形有两个点是复用的，所以参数不会呈现跳动。图11显现该办法作用很好。
文献[7]中说到能够选取许多点，然后选用最小二乘法进行拟合。可是因为各像素点失真程度纷歧样(越远离图画中心失真越严峻)，所以最终成果可能是原本失真较小的点被失真较大的点所“连累”，没有一个点是精确的。
状况(2)：摄像头俯角较大，跑道会呈现在图画各个方位(如图1(b)所示)，这时单片机需求对整幅图画进行处理。可运用下列办法。
这时不再让U=Xu，V=Yu，而是设
从图画中读出多个像素坐标(U，V)，令k初值为0.00001，经过式7解出(Xu，Yu)，依据式6经过最小二乘法解出 ，再依据式5求出(Xw，Yw)，求出拟合差错sum_err。(这儿要将式5与式6中的U、V别离换成Xu、Yu)。有关最小二乘法可参阅文献[8]。
将k累加0.00001，相同的过程可求出sum_err。
画出k与sum_err曲线，sum_err起先跟着k增大而减小，但从某个k开端又开端增大，k值即取拐点处的值。
定论
本文依据摄像头成像模型，导出逆透视改换公式，并依据两种状况别离给出处理计划。该处理计划便利可行，可供各参赛摄像头部队参阅。
