摘要
本文讨论一套处理芯片单元级电测验进程电源电流失效问题的办法。当选用QFN-MR(四边扁平无引线–多排引脚封装)的BiCMOS (双极互补金属氧化物半导体)芯片进入量产准备期时,电源电流失效是一个骑虎难下的制作难题。
本文介绍了数种不同的失效剖析办法,例如,数据剖析、试验设计(DOE)、流程图剖析、计算辅佐剖析和标杆剖析,这些剖析办法对确认问题的本源有很大的协助,然后运用计算工程东西逐渐滤除可变要素。
本项目找到了电流失效问题的本源,并选用了相应的处理办法,使电源电流失效发生率大幅下降,与首要竞争对手势均力敌。终究,这个项目只通过优化公司内部资源,就提高了封装测验整体良率,而没有添加额定制作本钱。
这些改善办法还提高了产品质量,下降了客户投诉质量问题的危险。在悉数处理办法执行到位后,跟着量产成功,该项目节约制作本钱38.25万美元。
1.0 前语
为了可以在技能快速改变的半导体工业中生计,不管是企业内部用户,仍是外部商场客户,半导体厂商有必要在客户心目中树立杰出的形象,这是半导体企业坚持商场竞争力和品牌价值所面对的最大应战。“满足度”是树立杰出客户联系的要害要素。相反,不能让客户满足的事务是无法继续下去的。
QFN-MR(四边扁平无引线–多排引脚封装)是意法半导体卡兰巴工厂产值的最大的产品,对公司财务成绩贡献率很高(依照全球评价规范)。
不过,为同一客户出产同一产品,有些外包厂(外包厂1和外包厂2)在产品质量上却更胜一筹,这迫使卡兰巴工厂有必要自我改善。
产品1是QFN-MR产品,在量产准备阶段,电测验电源电流总失功率不合格,总良率丢失到达5.2%。产品 1是意法半导体卡兰巴工厂的一个新产品线,需求给大客户留下交货快的形象,可是不能献身产品质量,因而,需求找到构成产品缺点的首要原因。事实上,处理这些问题将会给卡兰巴工厂量产相似产品渠道带来改进时机。
1.1 产品1装备
产品1是一款选用VPLGA封装的BiCMOS芯片,用于操控硬盘驱动器的电机运转。这儿VPLGA代表超薄格栅阵列四边扁平无引线–多排引脚塑料封装,封装厚0.90 mm,引脚88个。方针使用包含纤薄型电子设备和计算机硬盘驱动器的电机操控。
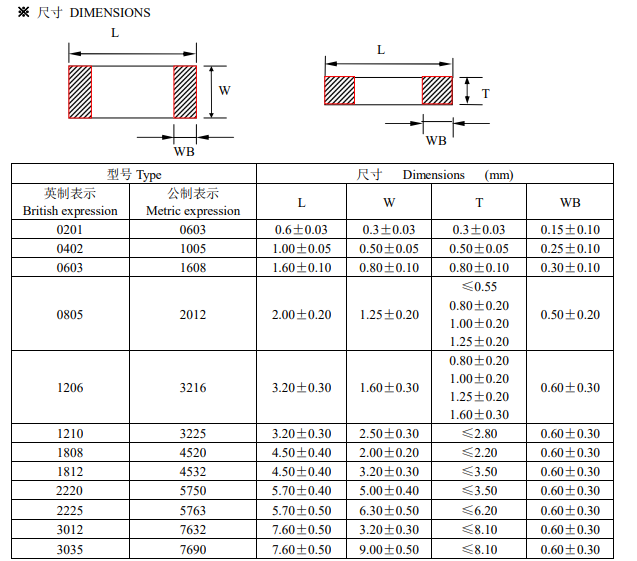
图1是产品1的封装示意图。

图1:VPLGA88产品装备 / POD
1.2 BiCMOS半导体制作技能

图2:BiCMOS半导体制作技能
BiCMOS芯片由五层组成。NiPd (镍钯金)是终究一层金属层,互连线就打在这一层上。
1.3 QFN-MR无胶带引线结构封装
无胶带四边扁平无引线封装是一种引线结构封装载体(渠道),利用后工序蚀刻,在载体上构成引脚面积。与其它的相似微型封装比较,无胶带QFN封装给意法半导体卡兰巴工厂带来更好实惠,例如,引线结构本钱低,支撑多排引脚,兼容铜线,无胶带载体,晶片切开速度快。

图3:无胶带QFN引线结构装备
1.4 产品1封测悉数流程

图4:1.4 产品1封装流程
图4所示是产品1的封装流程,该流程在产品开发和认证测验阶段制定,根据现有封装流程,选用相同的芯片制作技能和资料。
1.5 产品1线路应力体现
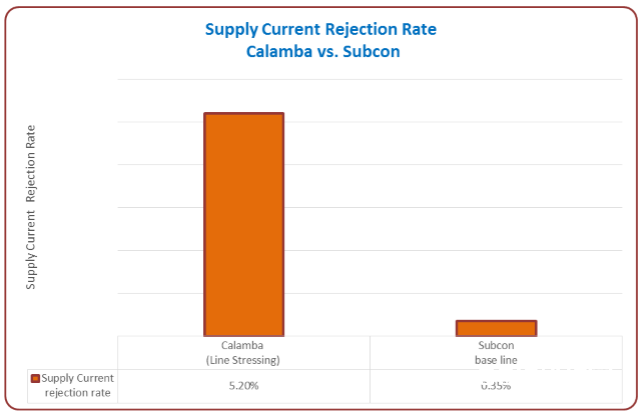
图5:电源电流按捺比比照
在产品1量产准备初期,终究测验的电源电流按捺比是5.20%,远超外包厂的0.35%。上面的柱形图是意法半导体卡兰巴工厂与外包厂的电源电流按捺比的比较图,两者之间的巨大距离对意法半导体卡兰巴工厂的未来事务开展构成严重要挟。
1.6 标杆剖析和比较剖析
运用标杆剖析和比较剖析法寻觅意法半导体卡兰巴与外包厂在产品制作上的不同之处。需求阐明的是,外包厂在水刀工序后还有烘烤工序。

图6:意法半导体与外包厂的制作流程比较
在开端剖析的时分,咱们发现烘烤工序是首要不同之处。在清洗等湿法工序后,需求进行烘烤工序,除去单元内
的湿汽。开端剖析成果显现,烘烤是终究测验电源电流失效的首要要素,便是这个巨大发现让项目组开端专心这个工序的探求。
同样地,项目组还做了微流程图,以确认项目探求规模。

图7:微流程图剖析/封装流程图
1.7 问题描绘
在量产准备期,产品1电源电流按捺比是 5.20%,被归为封装工序固有湿法工序构成的湿润性危险。
2.0 试验部分
2.1 资料:
§ 水刀
§ QFN无胶带引线结构封装
§ BiCMOS晶片
§ 塑料单元
§ 查看与测验设备
2.2 试验要点放在首要本源即水刀工序上:
确认问题本源并采纳相应的纠正办法至关重要,研讨方向首要放在湿法工序上,根据微流程图剖析,水刀工序最有可能是潜在变异的本源。
2.3 解剖水刀工序:
为更好地了解水刀工序,需求逐渐剖析记录点,调查从资料制备、装卸到查看的整个单元工序。


图8:水刀工序具体流程
2.4 辨认输入改变:
运用输入输出办法深挖改变要素。通过深入研讨,42个KPIV变量被确认为重要的X要素,如图9所示。(详图见附录A)

图9:输入-输出工作单
2.5 优先考虑因果联系:
运用因果(C&E)矩阵建立输入变量与X要素的内部联系,如图10所示。
(详图见附录B)

图10:因果矩阵