0 导言
正交频分复用(Orthogonal Frequency DivisionMultiplexing,OFDM)具有高速传输数据、高效的频谱使用率和抗多径的才能。最近几年,OFDM技能现已成功地应用在移动以及固定数据传输中,例如非对称数字用户线路(Asymmetric Digi-tal Subscriber Line,ADSL)、数字视频播送(DVB-T和DVB-H),以及无线局域网(WirelessLAN)等。现在,OFDM已被视为第四代移动通讯最具竞争力的传输技能。
因为OFDM在频域把信道分红许多正交子信道,各子信道的载波间坚持正交,且频谱彼此堆叠,这样就减小了子信道间的搅扰,进步了频谱使用率。所以,OFDM体系对频率偏移十分灵敏,很小的频率偏移都或许损坏子载波间的正交性,然后发生载波间搅扰(ICI)以构成体系功能的严峻下降。因而,在OFDM体系中,频率偏移估量的准确性至关重要。
1 OFDM体系及其同步要求
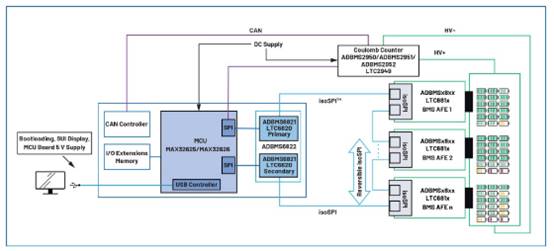
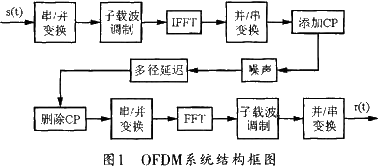
OFDM体系能有效地对立信道多径式微;它经过将串行数据流调制到并行的子载波上,可在很大程度上进步带宽使用率;而在传输的数据流码字中刺进循环前缀(CP),则能够有效地消除码间搅扰和载波间搅扰。图1所示是OFDM体系的简略结构。
OFDM多载波信号s(t)可写为如下的复数方式:![]()
式中,ωn=ω0+n△ω为第n个载波频率,dn(t)为第n个载波上的复数信号。
该技能首要对输入信号流进行调制(例如PSK或QAM),以将数据流经过IDFT调制到N个子载波上,然后经过IDFT使每个符号的后L个抽样被复制到符号前端以构成循环前缀,再经过信道传输,并在接纳端除掉循环前缀,接着将接纳到的符号经过DFT改换,这样就能康复传输信号。在信道上传输的信号或许会遭到噪声搅扰,这是因为接纳端和发送端的频率不匹配,此外,多普勒频移也会发生频率偏移。如不考虑信道式微的影响,接纳符号和发送符号之间的联系如下:![]()
式中,θ标明不知道的符号抵达时刻偏移,ε是不知道的载波频率偏移。假如循环前缀长度L大于信道冲击呼应,那么ISI就能够防止。
2 频率同步算法
由Jan-Japp提出的最大似然估量(ML)算法具有核算量小、冗余度低、算法完成简略、可一起估量守时和频偏的长处。但该算法的频率估量规模过小,守时估量较为粗糙,不能直接用到实践体系中。由ML算法估量的实践相对频差为:![]()
在上式中,n实践上无法确认,只能取:![]()
所以约束了ε的估量规模。
频偏估量时一般将频率偏移区分红分数部分和整数部分。这儿是以子载波距离作为归一化规范。子载波距离的整数倍的频偏称为整数部分频偏,剩下的小于一个子载波问隔的频偏称为分数部分频偏。整数频偏经IFFT改换后一般体现成对应子载波标号的偏移,而分数倍频偏则体现为相位的旋转。因为OFDM体系存在很多的提高功率的导频,因而,只需查找到这些导频就能够得到整数倍频率偏移,而检测导频的相位又能够得到分数倍频偏。估量到的频率差错除了要送到后一级以实时纠正数据的相位外,为了减小载波间搅扰,还必须将其前馈到时域进行频率校对,因而频偏的校对示意图可用图2来阐明。
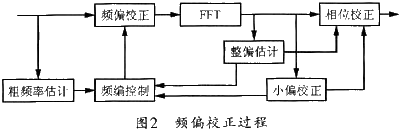
2.1 整数倍频偏估量
一般来说,整数倍频率同步的作用是对频率整数倍子载波距离部分进行估量。没有频偏时的频域信号Y(k)=FFT(y(n))=FFT(x(n)),现在假定频偏是m(为整数)倍的载波距离,则:y’(k)=FFT(x(n)ej2πm/N)=Y(k-m),可见,整数倍频偏的影响仅仅对频域数据进行了循环移位。
本文介绍的移动相关算法首要根据频域最大似然估量理论。现以DVB-T体系为例,每个OFDM符号在频域内都刺进了很多的被提高了功率的导频信号,其间接连导频在每个符号内的方位不变。因为时域同步部分对每个符号都进行了粗频率偏移校对,因而,当前后两个符号导频数据相关时,在正确的导频点将得到较大的功率。因为前后符号的数据点不相关,它们的相关值则近似为零。故可将接连的两个符号共扼相乘,然后将导频功率累加: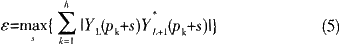
上式中,h导频的个数,pk是没有频率差错时第k个导频的方位,s是移动量,L是接连导频个数。s的改变规模是FFT给出符号同步的前c-1个数据到符号同步后的c个数据,ε取最大值可得到正确的导频方位,s-c便是整数倍频率差错即:m=s-c。
2.2 小数倍频偏估量
本文选用线性最小平方估量法进行小数倍频偏估量。在OFDM体系的接纳端,每个子载波在FFT处理时都可乘上解调因子:![]()
并由此得出实践的子载波解调频率:
实践的第m个子载波的解调频率为:![]()
式中,为载波频率f0,F=F0/N,N为子载波个数,F0为接纳机压控晶振输出的采样频率。由此能够看出,在第m个子载波上,载波频偏和采样钟偏移的联合效应是巨细等于△fm的子载波频偏,这儿:![]()
将整偏校掉后,△f0仅为小数倍的子载波距离。这个子载波频偏可使频域上接纳机已解调符号的第m个子载波比发射机的第m个子载波多乘一个因子e-j2π△fmt,即在频域上发生了一个相位旋转。由此可见,若没有ISI的影响,就能够经过对采样时钟偏移(△F0=F0'-F0)和小数倍频偏(△f0=f0-f0)所发生的相位之和进行联合估量。
一个符号中接连导频的方位是固定不变的,当前后两个符号的对应导频点相关时,就会得到前后两个符号对应导频点的小数倍频偏和采样时钟频偏所发生的相位差,该相位差可标明为: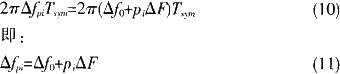
式中,Tsym为符号周期,pi为导频点方位,pi∈P,P为导频点方位调集,i=0,1,…,K-1,K是P的基数,△fpi为第Pi个导频点上相关成果的频率部分,这个值以下用△fpi标明,即估量成果。
假如设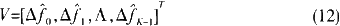
一起考虑在第pi个子载波上的估量差错ei,则有:![]()
式中,△fpi为在第pi个导频点上的小数倍频率偏移和采样钟频率偏移之和,现令:θ=[△f0,△F0]T为所需估量的向量参数,那么有: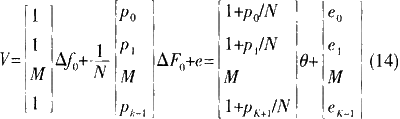
线性最小平方估量便是在给定的条件下,根据调查方程估量向量θ=[△f0,△F0]T的。根据最大似然估量原理,要使e2最小,相当于(V-Hθ)T(V-Hθ)应取最小值,因而可得到:![]()
可见,使用这种算法也能够一起估量出采样钟频率偏移。进一步研讨标明,该算法的估量差错很小,所以十分具有实用性。
2.3 仿真剖析
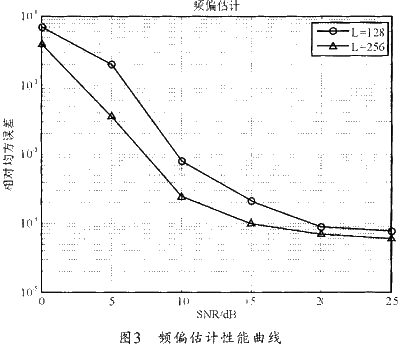
笔者在瑞利式微信道下对上述频率偏移估量办法进行仿真,关于频偏设置为0.1倍的子载波距离,采样钟频率偏移为100 ppm,若以L为维护距离长度,N=2048为一个符号的数据长度,其频偏估量功能曲线如图3所示。
3 结束语
从图3能够看出,估量差错小于0.01倍的载波隔要求的信噪比比较低,因而该算法完全能满意OFDM体系功能的要求。