开关电源变压器的涡流损耗在开关电源的总损耗中所占的份额很大,怎么下降开关电源变压器的涡流损耗,是开关电源变压器或开关电源规划的一个重要内容。变压器出产涡流损耗的原理是比较简单的,因为变压器铁芯除了是一种很好的导磁资料以外,一起它也归于一种导电体;当交变磁力线从导电体中穿过期,导电体中就会发生感应电动势,在感应电动势的效果下,在导电体中就会发生回路电流使导体发热;这种因为交变磁力线穿过导体,并在导体中发生感应电动势和回路电流的现象,人们把它称为涡流,因为它发生的回路电流没有作为能量向外输出,而是损耗在本身的导体之中。
单激式开关电源变压器的涡流损耗核算与双激式开关电源变压器的涡流损耗核算,在办法上是有差异的。但用于核算单激式开关电源变压器涡流损耗的办法,只需略微改换,就能够用于对双激式开关电源变压器的涡流损耗进行核算。例如,把双激式开关电源变压器的双极性输入电压,别离当作是两次极性不同的单极性输入电压,这样就能够完成关于双激式开关电源变压器涡流损耗的核算。因而,下面仅对单激式开关电源变压器的涡流损耗核算进行详细剖析。
当有一个直流脉冲电压加到变压器初级线圈的两头时,在变压器初级线圈中就就有励磁电流经过,并在变压器铁芯中发生磁场强度H和磁通密度B,两者由下式决议:
B =ΔB*t/τ +B(0) (2-44)
H =ΔH*t/ΔH +H(0) (2-45)
上式中ΔB和ΔH别离为磁通密度增量和磁场强度增量,τ为直流脉冲宽度,B(0)和H(0)别离为t = 0时的磁通密度B和磁场强度H。
传统的变压器铁芯为了下降涡流损耗,一般都把变压器铁芯规划成由许多薄铁片,简称为铁芯片,相互重迭在一起组成,而且铁芯片之间相互绝缘。图2-18表明变压器铁芯或变压器铁芯中的一铁芯片。咱们能够把这些铁芯片当作是由十分多的“线圈”(如图中虚线所示)紧密结合在一起组成;当交变磁力线从这些“线圈”中笔直穿过期,在这些“线圈”中就会发生感应电动势和感应电流,因为这些“线圈”存在电阻,因而这些“线圈”要损耗电磁能量。
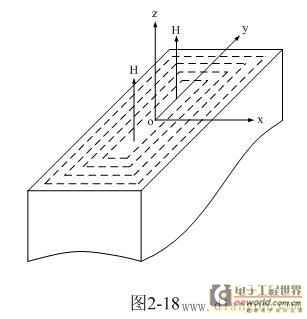
在直流脉冲效果期间,涡流的机理与正激电压输出的机理是根本相同的。涡流发生磁场的方向与励磁电流发生磁场的方向正好相反,在铁芯片的中心处去磁力最强,在边际去磁力为零。因而,在铁芯片中磁通密度散布是不均匀的,即最外层磁场强度最大,中心处最小。假如涡流退磁效果很强,则磁通密度的最大值或许远远超越其均匀值,该数值由已知脉冲的起伏和宽度来决议。
沿铁芯片截面的磁场散布,能够用麦克斯韦的方程式来求得;麦克斯韦的微分方程式为:


上式中 μa为变压器铁芯的均匀导磁率,ρc为铁芯的电阻率,负号表明涡流发生的磁场方向与励磁电流发生的磁场方向相反。rot E和rot Hx别离表明电场和磁场的旋度,即涡旋电场和涡旋磁场的强度。Hx、Hy、Hz别离磁场强度H的三个重量;Bx、By、Bz别离磁感应强度B的三个重量;Ex、Ey、Ez别离电场强度H的三个重量。
因为单激式开关电源变压器铁芯的磁滞回线面积很小,其磁化曲线根本上能够当作一根直线,导磁率μ也能够当作是一个常数;因而,这儿运用均匀导磁率 来替代含义广泛的导磁率 。
从图2-18能够看出,磁场强度由H = Hz:和Hx = Hy = 0组成;关于电场强度,其指向平行于Y轴为E = Ey,Ex = Ez = 0。因而,上面两式又能够改写为:

对(2-53)式进行微分,然后代入(2-52)式,即可求得磁场强度的一维散布方程为:

因为加到变压器初级线圈两头的电压是一个直流脉冲方波,在安稳状况条件下,励磁电流发生的磁场强度或磁通密度的增加应与时刻成线性关系,即:

当x = 0时,正好坐落铁芯片的中心,此处的磁场强度最小,即此点的导数值等于0,由此求得积分常数c1= 0。
对(2-57)再进行一次积分得:
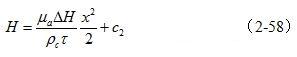
因为在变压器铁芯片内,截面磁场强度的均匀值Ha,在任一时刻内都必须等于电磁感应所要求的值,即满意(2-45)式的要求,因而对应图2-18对(2-58)式求均匀值得:
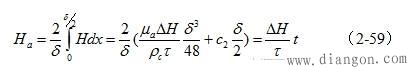
把(2-60)代入(2-58)式,可求得在安稳状况条件下铁芯片中的磁场强度为:
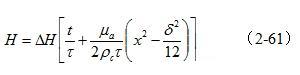
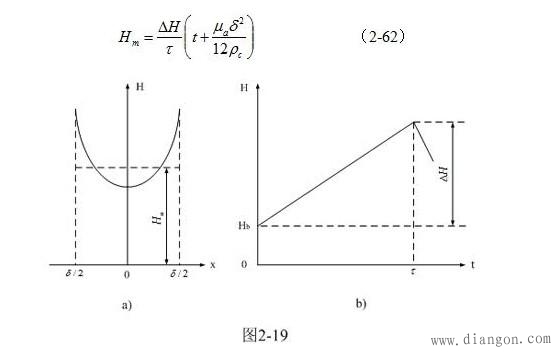
图2-19-a和图2-19-b别离是由(2-61)式给出的,铁芯片中磁场强度按水平方向散布的函数H(x)和按时刻散布的函数H(t)曲线图。
从图2-19-a中能够看出,因为涡流发生反磁化效果的原因,在铁芯或铁芯片中心磁场强度最低,而边际磁场强度最高。
在图2-19-b中,跟着时刻线性增加部分是变压器初级线圈励磁电流发生的磁场;Hb是为了补偿涡流发生的去磁场,而由变压器初级线圈别的供给电流所发生的磁场。
从图2-19-b能够看出,涡流损耗对变压器铁芯中磁场强度(均匀值)的影响,与变压器正激输出时,次级线圈中电流发生的磁场对变压器铁芯磁场的影响,根本是相同的。值得注意的是,假如用相同办法对y轴方向进行剖析,也能够得到相同的成果。
从图2-19-a能够看出,当x =δ/2 时,铁芯片外表磁场强度的最大值为: